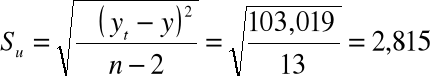Algorytm analizy korelacji i regresji liniowej dwóch zmiennych jest następujący:
Specyfikacja zmiennych.
Na podstawie kryteriów merytorycznych określamy:
zmienną objaśnianą - (Y),
zmienną objaśniającą - (X).
Sporządzenie korelacyjnego diagramu rozrzutu.
Na jego podstawie wnioskujemy, czy związek korelacyjny występuje oraz czy można przyjąć, że jest to związek liniowy.
Określenie siły i kierunku związku korelacyjnego między badanymi zmiennymi.
Zakładamy przy tym, że:
związek korelacyjny występuje,
jest to związek o kształcie liniowym.
Wtedy jako miarę siły i kierunku zależności między badanymi zmiennymi stosujemy współczynnik korelacji liniowej Pearsona r .
Estymacja parametrów liniowych funkcji regresji i ich prezentacja graficzna.
Szacowanie parametrów funkcji regresji:
![]()
gdzie:
xt - wartości zmiennej objaśniającej ( t = 1, 2, ..., N ),
ay - wyraz wolny,
by - współczynnik regresji Y względem X.
Współczynnik regresji by ma swoją interpretację. Określa on mianowicie o ile przeciętnie biorąc zmieni się Y, gdy zmienna X wzrośnie o jednostkę.
Korzystając z KMNK otrzymuje się, że:
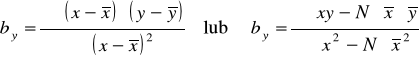
Można też obliczyć współczynnik regresji wykorzystując obliczony wcześniej współczynnik korelacji liniowej r:
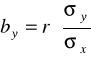
Natomiast wyraz wolny liczymy ze wzoru:
![]()
Współczynnik regresji by ma swoją interpretację. Pokazuje mianowicie o ile przeciętnie biorąc zmieni się zmienna Y, jeśli zmienna X wzrośnie o jednostkę.
Szacowanie parametrów funkcji regresji:
![]()
gdzie:
yt - wartości zmiennej Y dla t = 1, 2, ..., N,
ax - wyraz wolny,
bx - współczynnik regresji X względem Y.
Współczynnik regresji bx ma również swoją interpretację. Pokazuje mianowicie o ile przeciętnie biorąc zmieni się X, jeśli Y wzrośnie o jednostkę.
Wykorzystując KMNK otrzymuje się, że:
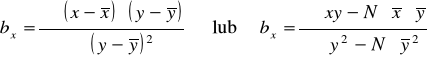
Lub podobnie jak w przypadku poprzedniej funkcji:
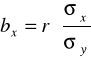
Natomiast wyraz wolny liczymy ze wzoru:
![]()
.
Oceniamy „jakość” wyznaczonych funkcji. W tym celu liczymy:
odchylenie standardowe składnika resztowego Su:
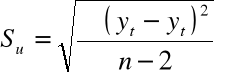
![]()
2. współczynnik zmienności resztowej Vu:
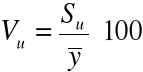
3. współczynnik determinacji R2 :
![]()
4. współczynnik zbieżności (indeterminacji)
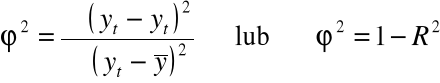
5. Błędy średnie szacunku ocen parametrów funkcji regresji:
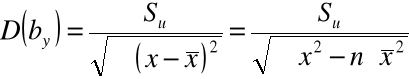
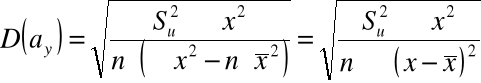
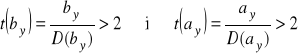
c.d. zadania z pliku „Kowariancja”
Wyznaczamy parametry liniowej funkcji regresji zużycia maszyny |
||||
względem czasu jej użytkowania: |
|
|
|
|
![]()
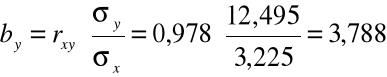
![]()
Funkcja regresji II rodzaju zmiennej y względem zmiennej x ma więc postać:
![]()
Interpretujemy współczynnik regresji by:
Jeżeli okres użytkowania maszyny (x) wzrasta o 1 rok to jej zużycie (y) |
||||
wzrasta przeciętnie o 3,79 %.
Liczymy teoretyczne wartości zmiennej y, zgodnie z wyznaczoną funkcją regresji (kolumna z czerwonymi liczbami): Nr Czas eksploatacji w latach (x) Zużycie w % (y) x2 y2 x*y
Reszty:
1 7 27 49 729 189 27,58 -0,58 0,33
2 2 6 4 36 12 8,63 -2,63 6,94
3 6 28 36 784 168 23,79 4,21 17,74
4 9 33 81 1089 297 35,15 -2,15 4,64
5 2 8 4 64 16 8,63 -0,63 0,40
6 4 12 16 144 48 16,21 -4,21 17,74
7 3 12 9 144 36 12,42 -0,42 0,18
8 1 8 1 64 8 4,85 3,15 9,95
9 11 45 121 2025 495 42,73 2,27 5,15
10 10 40 100 1600 400 38,94 1,06 1,12
11 4 13 16 169 52 16,21 -3,21 10,31
12 8 32 64 1024 256 31,37 0,63 0,40
13 5 17 25 289 85 20,00 -3,00 9,00
14 2 10 4 100 20 8,63 1,37 1,86
15 1 9 1 81 9 4,85 4,15 17,25
75 300 531 8342 2091
0,00 103,02
|
|
|
|
|
Oceniamy "jakość" funkcji regresji, czyli musimy odpowiedzieć na pytanie: |
|||||
Czy wyznaczona funkcja dobrze opisuje zależność między badanymi |
|
||||
zmiennymi?
W tym celu liczymy: 1) odchylenie standardowe składnika resztowego:
|
|
|
|
|
|
Można też zastosować wzór uproszczony wzór uproszczony:
![]()
Komentarz: Rzeczywiste zużycie maszyny różni się przeciętnie od zużycia wyznaczonego za pomocą funkcji regresji o +/- 2,815 %. |
|||
|
|
|
|
2) współczynnik zmienności resztowej:
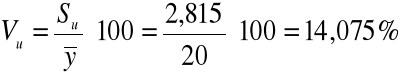
3) Współczynnik determinacji:
![]()
4) Liczymy błędy średnie szacunku parametrów funkcji regresji:
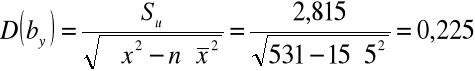
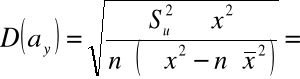
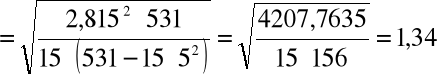
Można więc funkcję regresji zapisać następująco:
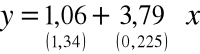
![]()
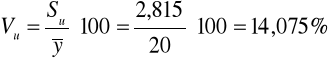
![]()
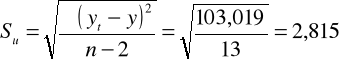
![]()
![]()
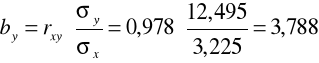
![]()
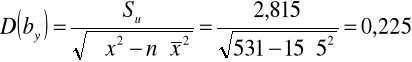
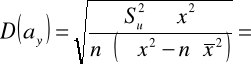
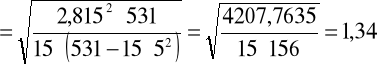
![]()
Wyszukiwarka
Podobne podstrony:
ANALIZA KORELACJI I REGRESJI-wzory, Statystyka, statystyka(3)
Analiza korelacji i regresji, studia, statystyka
Analiza korelacji i regresji, Statystyka opisowa i matematyczna
statystyka, Korelacja i regresja liniowa, Korelacja i regresja liniowa
Analiza korelacji i regresji 3, STATYSTYKA (WYK?AD 16
Analiza korelacji i regresji 3, STATYSTYKA (WYK?AD 16
STATYSTYKA - analiza korelacji i regresji, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
ANALIZA KORELACJI I REGRESJI”, Statystyka, statystyka(3)
zadanie 2- regresja liniowa, Statyst. zadania
06.regresja liniowa, STATYSTYKA
Elementy analizy korelacji i regresji
KOLOKWIUM Z ANALIZY STRUKTURY TEMAT X 2004, Statystyka Opisowa UG
więcej podobnych podstron