1. Wyjaśnić pojęcie czystego zginania.
Czyste zginanie (rys. poniżej) zachodzi wtedy, gdy w danym przedziale długości belki moment gnący jest stały, tzn., gdy siła tnąca równa się zero (T=0).Przy obliczeniach opieramy się na dwóch hipotezach:
Hipoteza 1.: Wszystkie przekroje odkształconej belki, które były płaskie przed odkształceniem, pozostaną płaskie po odkształceniu podczas czystego zginania (jest to tzw. hipoteza płaskich przekrojów).
Hipoteza 2.: W pręcie poddanym czystemu zginaniu poszczególne warstwy równoległe do (zakrzywionej) osi pręta, a prostopadłe do płaszczyzny zginania, znajdują się w jednokierunkowym stanie naprężenia, tzn. są wyłącznie rozciągane, bądź ściskane i nie wywierają na siebie nawzajem żadnych nacisków poprzecznych (wzdłuż promienia krzywizny (ၲ)).
2. Koło Mohra dla naprężeń (2D).
Koło Mohra pozwala odczytać wartości momentów Iy, Iz i Iyz dla układu obróconego o dowolny kąt a względem układu głównego, albo wartości ekstremalne momentów. Jest to również wykreślna metoda wyznaczania stanu naprężenia.
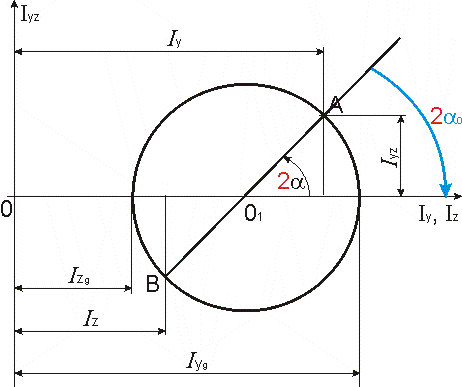
3. Definicja wyboczenia.
Przy ściskaniu osiowym pręta istnieje taki poziom siły ściskającej, nazywany siłą krytyczną, przy którym jej nieskończenie mały przyrost spowoduje ugięcie pręta w kierunku prostopadłym do jego osi. Zjawisko to nazywa się wyboczeniem
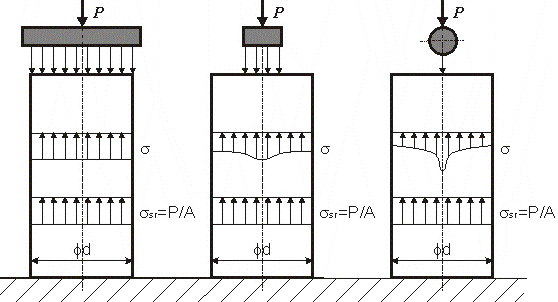
4. Zasada de Saint Venanta.
Jeżeli na pewien niewielki obszar ciała sprężystego pozostającego w równowadze działają kolejno rozmaicie rozmieszczone, ale statycznie równowarte obciążenia, to w odległości od obszaru przewyższającej wyraźnie jego rozmiary powstają praktycznie jednakowe stany naprężenia i odkształcenia (zasada sprężystej równoważności).
5. Definicja siły tnącej.
Siłą tnącą (poprzeczną) (T) w danym przekroju elementu (belki) nazywa się sumę rzutów wszystkich sił działających po jednej stronie przekroju na kierunek styczny do tego przekroju
6. Definicja momentu gnącego.
Momentem gnącym w danym przekroju poprzecznym elementu (belki) nazywa się składową styczną wektora momentu wszystkich sił działających po jednej stronie tego przekroju, względem jego środka ciężkości
Momentem skręcającym w danym przekroju poprzecznym elementu (wału) nazywa się składową normalną wektora momentu wszystkich sił działających po jednej stronie tego przekroju, względem jego środka ciężkości
7. Definicja siły normalnej.
Siłą (wewnętrzną) normalną (N) w danym przekroju elementu (pręta) nazywa się sumę rzutów wszystkich sił działających po jednej stronie przekroju na kierunek normalny do tego przekroju
8. Warunek wytrzymałości na skręcanie.
gdzie:
s - naprężenia styczne skręcające w [Pa],
M - moment skręcający przekrój w [Nm],
Wo - wskaźnik wytrzymałości przekroju na skręcanie [m3],
ks - naprężenia dopuszczalne na skręcanie w [Pa]
9. Warunek wytrzymałości na zginanie.
gdzie:
σg - naprężenia normalne zginające w [Pa],
M - moment zginający przekrój w [Nm],
Wx - wskaźnik wytrzymałości przekroju na zginanie [m3],
kg - naprężenia dopuszczalne na zginanie w [Pa]
10. Warunek wytrzymałości na rozciąganie lub ściskanie.
gdzie:
σ- naprężenia normalne w [Pa]
F - siła w [N],
S - przekrój na który działa siła F wyrażony w [m2],
k - naprężenia dopuszczalne na rozciąganie (kr), ściskanie (kc) w [Pa]
11. Warunek wytrzymałości na ścinanie.
gdzie:
τt - naprężenia styczne w [Pa],
F - siła w [N],
S - przekrój na który działa siła F wyrażony w [m2],
kt - naprężenia dopuszczalne na ścinanie w [Pa]
12. Moment zastępczy.
W przypadku pręta (wału), który w „niebezpiecznym” przekroju jest zginany momentem Mg i skręcany momentem Ms hipotezy: Hubera i tmax pozwalają określić tzw. momenty zastępcze, które umożliwiają sprowadzenie całego zagadnienia do prostego zginania.
Naprężenia w najbardziej wytężonym punkcie A rozważanego przekroju, to:
![]()
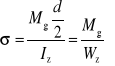
Oraz
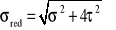
Naprężenia zredukowane (zastępcze) w rozważanym przypadku według hipotezy tmax wynoszą:
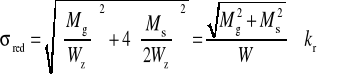
co można zapisać , jako:
Licznik ostatniego ułamka nazywa się momentem zastępczym (Mz) według hipotezy tmax :
![]()
Naprężenia zredukowane (w rozpatrywanym przypadku) według hipotezy Hubera:
![]()
,
![]()
stąd:
W obu powyższych przypadkach warunek wytrzymałościowy ma postać:
![]()
13. Naprężenia zredukowane według hipotezy HMH.
miarą wytężenia jest właściwa energia odkształcenia postaciowego,
lub:
wytężenia w dwóch różnych stanach naprężenia są równe, jeśli energie właściwe odkształcenia postaciowego są równe w tych stanach.
![]()
14. Naprężenia zredukowane według hipotezy Tresci.
miarą wytężenia materiału jest największe naprężenie styczne (tmax)
![]()
Hipoteza ta zapewnia dużą zgodność z doświadczeniem, szczególnie dla materiałów sprężysto-plastycznych (np. stal niskowęglowa); jest ona szeroko stosowana na równi z hipotezą Hubera-von Misesa-Hencky'ego, dającą najlepszą zgodność z doświadczeniem.
16. Wykres Woehlera.
Wykres zależności pomiędzy wartością naprężeń niszczących próbkę danego materiału i ilością cykli zmian obciążenia tej próbki.
17. Siła krytyczna przy wyboczeniu według Eulera.
Zagadnienie wyznaczenia wartości dla Pkr dla ściskanego pręta prostego rozwiązał Euler, rozpatrując równowagę pręta w postaci wyboczonej.
Wyboczenie następuje w płaszczyźnie najmniejszej sztywności giętnej (EImin).
Pręt jest wówczas nie tylko ściskany, ale też zginany momentem Mg(y)=Py. Zależność tego momentu od współrzędnej x jest nieliniowa, dlatego nie wolno tu stosować zasady superpozycji. Wzór na tzw. eulerowską siłę krytyczną (wzór Eulera).
![]()
![]()
W zależności od sposobu zamocowania pręta rzeczywistą długość pręta (l) zastępuje się tzw. długością wyboczeniową lw , wprowadzając współczynnik sposobu zamocowania pręta (ၭ):
18. Definicja smukłości pręta ściskanego.
Smukłość pręta λ jest to stosunek długości zredukowanej pręta do promienia bezwładności przekroju poprzecznego.
19. Współczynnik sposobu zamocowania pręta przy wyboczeniu (przykłady).
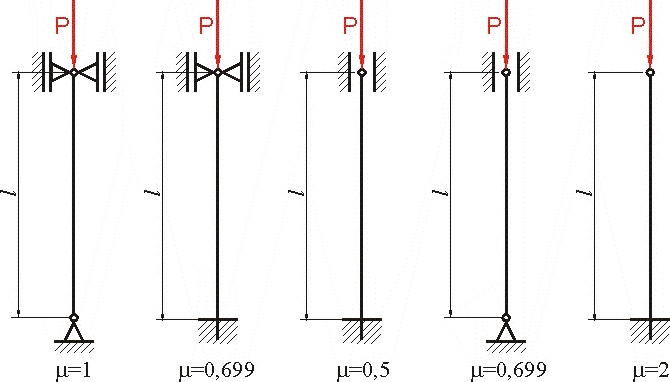
21. Współczynnik asymetrii cyklu.
Współczynnik asymetrii cyklu R opisuje niesymetryczność cyklu zmęczeniowego i jest równy: ![]()
22. Wyraźna granica plastyczności.
Naprężenie niezbędne do zapoczątkowania makroskopowego odkształcenia plastycznego we wszystkich ziarnach. Wyraźna granica plastyczności określona jest wzorem:
Re- naprężenie w granicy plastyczności
Fe- siła obciążająca próbkę w granicy plastyczności
S0- początkowe pole przekroju próbki
Dla większości metali i stopów (stale o zaw. C pow. 0,4%, stale stopowe, miedź, aluminium i ich stopy)nie obserwuje się wyraźnej granicy plastyczności
![]()
![]()
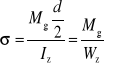
![]()
![]()
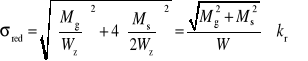
![]()
![]()
![]()
![]()
![]()
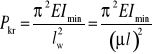
Wyszukiwarka
Podobne podstrony:
POLITECHNIKA LUBELSKA, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, MATERIAŁOZNAS
POLITECHNIKA LUBELSKA, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, MATERIAŁOZNAS
rozcuzu2, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
Metoda prądów oczkowych, Politechnika Lubelska, Studia, sem III, materiały, Teoria Obwodów1, kabelki
rfizyczn, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
stnaprez, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
GEOMPRZE, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
nr wykl, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
bnsp kom, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
mimorozc, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
rozcuzup, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
Mechpek2, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
podstaw1, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
Laboratorium elektroniki - Ćwiczenie 02, Politechnika Lubelska, Studia, sem III, materiały, Teoria O
mimroz e, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
belki, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
więcej podobnych podstron