dr Anna Barbaszewska-Wiśniowska

CIĄGI LICZBOWE

Zad.1. Uzupełnij:

a.

b.

c.

d.

Zad.2. Udowodnij z definicji, że
a następnie wskaż dla
istniejące
.

Zad.3. Czy prawdziwe są lematy:

a.

b.

Zad.4. Sformułuj twierdzenie o granicy sumy ciągów zbieżnych, a następnie wykaż je korzystając z definicji granicy ciągu.

Zad.5. Korzystając z twierdzeń o arytmetyce granic oblicz granice ciągów:

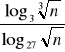
verte

Zad.6. Korzystając z twierdzenia o trzech ciągach oblicz granice ciągów:

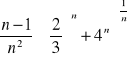
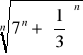
wsk.

Zad.7. Korzystając z definicji liczby e oblicz granice ciągów:

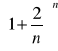
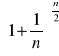
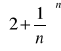
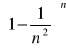
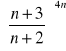
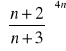
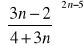
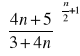
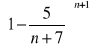
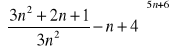
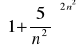
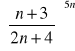
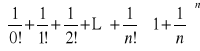
Zad.8. Oblicz granice ciągów.

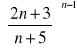
Zad.9. Uzasadnij, że następujące ciągi są zbieżne do zera

;
;
;
;

Zad.10. Udowodnij, że
korzystając ze wzoru dwumianowego Newtona i porównaj ten dowód z dowodem przedstawionym na wykładzie.

Zad.11. Wykaż, że ciąg
określony wzorem rekurencyjnym jest zbieżny a następnie wyznacz jego granicę

a.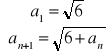

b.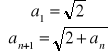

Zad.12.

a. Spośród ciągów
dobierając odpowiednio k wybierz ten, który zmierza do czterech

b. Udowodnij z definicji, że granicą wybranego ciągu jest liczba 4

c. Udowodnij, że każdy z pozostałych ciągów ma granicę mniejszą od 4

Zad.13. Oblicz
gdzie

verte

Zad.14. Udowodnij twierdzenie o trzech ciągach.

Zad.15. Wyjaśnij zastosowanie twierdzenia o trzech ciągach w dowodzie faktu, że

Zad.16. Zastosuj nierówność Bernoulliego i twierdzenie o trzech ciągach do obliczenia granicy ciągu
, a następnie wyjaśnij dlaczego nie można w analogiczny sposób wyznaczyć granicy ciągu

---