Politechnika Krakowska Fizyka Techniczna II Rok |
Marcin Bernady |
Rok akad.: 1999/2000 |
Data: 9.11.1999 |
||
Grupa 2 Zespół 3 |
|
Nr ćwicz.: 33 |
Ocena:
|
Podpis:
|
|
Zastosowanie Fotoogniwa do Pomiarów Fotometrycznych
Odróżniamy trzy główne rodzaje zjawisk fotoelektrycznych:
zjawisko fotoelektryczne zewnętrzne, polegające na emisji elektronów przez ciała naświetlane promieniowaniem elektromagnetycznym o dostatecznie dużej energii kwantów E = hν. Prawa rządzące tym zjawiskiem podał Einstein, a wyzyskano je w budowie fotokomórki;
zjawisko fotoelektryczne wewnętrzne, które polega na zwiększaniu przewodnictwa półprzewodników pod wpływem naświetlania; zostało ono wykorzystane do budowy fotooporów;
zjawisko fotoelektryczne zaporowe, polegające na tym, że na powierzchni granicznej między półprzewodnikiem a metalem gromadzą się pod wpływem naświetlania elektrony przewodnictwa. Warstewka ta, zwana warstwą zaporową, przepuszcza elektrony tylko w jednym kierunku. Jednym z rodzajów fotoogniw fotoelektrycznych jest fotoogniwo selenowe.
Górna elektroda jest bardzo cienką warstewką ołowiu napyloną na warstewkę selenu. Selen znajduje się na podstawie żelaznej. Jeżeli obie elektrody ogniwa połączymy obwodem zewnętrznym i oświetlimy półprzezroczystą warstewkę Pb, wówczas w obwodzie popłynie prąd od selenu ku Pb. Mechanizm działania ogniwa jest następujący: pod wpływem światła z warstwy Se wysyłane są elektrony. Powierzchnia styku pomiędzy Pb i Se ma działanie prostujące, pozwala przechodzić elektronom tylko od Se do Pb. W rezultacie wysyłane przez selen elektrony mogą poruszać się poprzez warstwę tylko w jednym kierunku, dając w obwodzie zewnętrznym prąd.
Za wielkość podstawową przyjmuje się w fotometrii światłość I źródła światła. Jednostką światłości jest 1 kandela [cd]. Jedna kandela jest 1/60 światłości wypromieniowanej w kierunku prostopadłym przez 1 cm2 ciała doskonale czarnego w temperaturze krzepnięcia platyny pod ciśnieniem 1,013⋅105 [N/m2].
Strumień świetlny Φ wysyłany równomiernie we wszystkich kierunkach przez punktowe źródło światła o światłości I w kąt bryłowy ω wynosi Φ = Iω. Wobec tego takie źródło światła wysyła w pełny kąt bryłowy strumień Φ = 4πI. Jednostką strumienia świetlnego jest 1 lumen [lm]. Jeden lumen jest to strumień świetlny wysyłany w kąt bryłowy równy 1 steradianowi przez punktowe źródło światła o światłości 1 cd.
Oświetleniem E powierzchni dS, na którą pada prostopadle strumień światła dΦ, nazywamy
![]()
Jednostką oświetlenia jest 1 lux [lx]. Jeden lux jest to oświetlenie, jakie sprawia strumień światła równy 1 lumenowi równomiernie rozłożony na powierzchni 1 [m2].
Jeżeli przez jednorodny, przezroczysty ośrodek biegnie równoległa wiązka promieni prostopadle do powierzchni płaskorównoległej płyty, ulega ona wówczas osłabieniu zgodnie z równaniem
![]()
gdzie:
J0 - gęstość strumienia energii w wiązce wnikającej w płytę, tzn. ilość energii przechodzącej w czasie 1 s przez powierzchnię 1 m2 przy kącie padania 0° [W/m2]
J - gęstość strumienia po przejściu przez warstwę ośrodka grubości d
- współczynnik absorpcji [m-1]
Wiązka światła białego jest mieszaniną promieniowań o różnych długościach fali i różnych współczynnikach absorpcji. Promieniowanie widzialne różnych barw jest w szkle w przybliżeniu jednakowo absorbowane, gdyż wiązka światła białego po przejściu przez płytę szklaną pozostaje nadal bezbarwna. Natomiast bardzo skąpe promieniowanie ultrafioletowe i bardzo obfite promieniowanie podczerwone zawarte w świetle żarówki są przez płytki szkła ołowianego paru mm w zupełności pochłonięte. Wynik pomiaru daje nam średni współczynnik absorpcji promieniowania widzialnego.
Wykonanie ćwiczenia
Pomiar 1
Badanie zależności wychylenia galwanometru x od oświetlenia E fotoogniwa. Oświetlenie
![]()
gdzie I jest światłością źródła, zaś r jego odległością od fotoogniwa. Zmianę oświetlenia uzyskujemy przez zmianę odległości źródła światła od fotoogniwa, przy stałej wartości światłości źródła I.
Wyniki pomiarów zamieszczam poniżej.
Lp |
r [m] |
1/r2 [m-2] |
x [dz] |
1 |
0,40 |
6,25 |
76,0 |
2 |
0,45 |
4,94 |
63,0 |
3 |
0,50 |
4,00 |
53,5 |
4 |
0,55 |
3,30 |
45,0 |
5 |
0,60 |
2,78 |
38,5 |
6 |
0,65 |
2,37 |
33,0 |
7 |
0,70 |
2,04 |
29,0 |
8 |
0,75 |
1,78 |
27,0 |
9 |
0,80 |
1,56 |
25,0 |
10 |
0,85 |
1,38 |
24,0 |
11 |
0,90 |
1,23 |
22,0 |
12 |
0,95 |
1,10 |
19,5 |
13 |
1,00 |
1,00 |
17,5 |
14 |
1,05 |
0,90 |
16,0 |
15 |
1,10 |
0,83 |
14,0 |
16 |
1,15 |
0,76 |
13,5 |
17 |
1,20 |
0,69 |
12,0 |
18 |
1,25 |
0,64 |
10,0 |
19 |
∞ |
0 |
0 |
Rysując wykres zależności uwzględniłem wartości z tabeli od numeru 11, gdyż w doświadczeniu używaliśmy żarówki, która nie jest źródłem punktowym, ale w przybliżeniu dla dużych odległości możemy potraktować ją jako źródło punktowe.
Wykres zależności zamieszczam w załączniku, którego równanie wynosi:
![]()
Obliczam czułość oświetleniową fotoogniwa
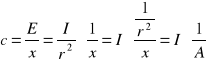
![]()
Błędy:
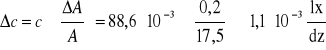
Czułość oświetleniowa fotoogniwa wynosi c = (88,6 ± 1,1)⋅10 -3 lx/dz.
Pomiar 2
Wyznaczanie współczynnika absorpcji promieniowania żarówki dla szkła ołowiowego.
Grubość płytek szklanych są kolejnymi wielokrotnościami 1,05 cm.
d [cm] |
x [dz] |
ln x |
0 |
90,0 |
4,50 |
1,05 |
69,6 |
4,24 |
2,10 |
57,0 |
4,04 |
3,15 |
47,5 |
3,86 |
4,20 |
39,0 |
3,66 |
5,25 |
33,0 |
3,49 |
6,30 |
28,5 |
3,35 |
7,35 |
23,5 |
3,16 |
8,40 |
20,0 |
3,00 |
Wykres zależności zlogarytmowanego wychylenia galwanometru od grubości próbek szklanych przedstawia się następująco:
![]()
Współczynnik absorpcji jest współczynnikiem kierunkowym danej prostej, gdyż zgodnie ze wzorem
![]()
ale x ∼ J0 zatem możemy napisać
![]()
Zaś po zlogarytmowaniu otrzymamy równanie liniowe, którego współczynnikiem kierunkowym jest właśnie μ.
Współczynnik absorpcji dla badanych próbek szkła wynosi μ = (0,168 ± 0,003) m -1
1
3
G
Pb
Fe
warstwa
zaporowa
Se
![]()
Wyszukiwarka
Podobne podstrony:
33 Bernady 1, Mieszanka WIŚ, Fizyka Wiś Iś
40 Bernady (2), Mieszanka WIŚ, Fizyka Wiś Iś
25 Bernady, Mieszanka WIŚ, Fizyka Wiś Iś
39 Bernady (2), Mieszanka WIŚ, Fizyka Wiś Iś
53 Bernady 2 (2), Mieszanka WIŚ, Fizyka Wiś Iś
31 Bernady (2), Mieszanka WIŚ, Fizyka Wiś Iś
40 Bernady (2), Mieszanka WIŚ, Fizyka Wiś Iś
40 Balawender (2), Mieszanka WIŚ, Fizyka Wiś Iś
14B (2), Mieszanka WIŚ, Fizyka Wiś Iś
opracowanie34 (2), Mieszanka WIŚ, Fizyka Wiś Iś
więcej podobnych podstron