Powietrze wilgotne

1. Podstawowe pojęcia powietrza wilgotnego

Przyjmuje się zwykle, że powietrze wilgotne o niskich ciśnieniach, stanowiące czynnik termodynamiczny w systemach cieplnych, jest roztworem powietrza suchego traktowanego jako gaz jednorodny i wilgoci. Wilgoć w powietrzu może występować w fazie gazowej jako para, równocześnie w fazie parowej i ciekłej w postaci drobnych kropel (mgły) lub w fazie parowej i stałej w postaci zawiesiny lodu (mgła śnieżna). Cechą charakterystyczną powietrza wilgotnego jest możliwość zmiany zawartości wilgoci i zmiany fazy wilgoci zawartej w powietrzu podczas przemian powietrza. W tej sytuacji udział składników powietrza wilgotnego (powietrza suchego i wilgoci), odniesiony do ilości roztworu, nie może jednoznacznie określać składu powietrza.

1. Wielkości określające udział wilgoci w gazie

W powietrzu wilgotnym niezmienna jest masa powietrza suchego i dlatego uniwersalnym wskaźnikiem składu powietrza jest zawartość wilgoci (stopień zawilżenia) x, tj.

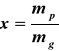
(1)

która jest równa stosunkowi masy wilgoci zawartej w powietrzu (w postaci pary, wody lub lodu) do masy powietrza suchego. Zawartość wilgoci x jest podstawowym parametrem powietrza wilgotnego. Określa ona ilość wilgoci zawartą w masie (1 + x) kg powietrza wilgotnego.

Masa gazu wilgotnego m jest sumą masy powietrza suchego m_g i masy zawartej w nim wilgoci m_p, co można zapisać:

(2)

przy czym

(3)

Z ostatniego równania wynika, że masa gazu wilgotnego odniesiona do ilości gazu suchego m_g zawartego w gazie wilgotnym jest masą ilości (1 + x) kg gazu wilgotnego. 1lość (1 + x) kg gazu wilgotnego stanowi podstawową jednostkę ilości substancji gazu wilgotnego.

Podobnie można postąpić z innymi parametrami gazu wilgotnego, odnosząc je do ilości gazu suchego m_g zawartego w gazie wilgotnym i otrzyma się wtedy parametry właściwe na jednostkę (1+ x) kg powietrza wilgotnego, co oznacza, że są to parametry masy (1 + x) kg powietrza wilgotnego. Takie parametry właściwe opatruje się zwykle indeksem 1+x, np. entalpia właściwa powietrza wilgotnego i_1+x, energia wewnętrzna właściwa - u_1+x, objętość właściwa - v_1+x.

Powietrze zawierające wilgoć tylko w postaci gazowej (pary) nosi nazwę powietrza niedosyconego. Jeśli zawarta w powietrzu wilgoć występuje równocześnie w fazie gazowej i ciekłej lub gazowej i stałej, to jest to powietrze zamglone (z mgłą wodną lub mgłą śnieżną).

Powietrze wilgotne w przypadku niezbyt wysokiej temperatury i pod niezbyt wysokim ciśnieniem, zawierające wilgoć wyłącznie w fazie gazowej, może być traktowane jako roztwór gazów doskonałych. Takie właśnie powietrze wilgotne będzie rozpatrywane. Konsekwencją założenia, że zarówno powietrze suche, jak i zawarta w nim para są gazami doskonałymi, jest możliwość stosowania równania Clapeyrona i prawa Daltona. To ostatnie określa ciśnienie roztworu jako sumę ciśnień cząstkowych:

(4)

gdzie:

p - ciśnienie powietrza wilgotnego, Pa,

p_p - ciśnienie cząstkowe pary, Pa,

p_g - ciśnienie cząstkowe gazu suchego, Pa.

W zależności od zawartości pary wodnej w powietrzu ciśnienie cząstkowe pary w powietrzu p_p może się zmieniać od zera, jeżeli zawartość wilgoci jest równa zero, do wartości maksymalnej równej ciśnieniu nasycenia pary, odpowiadającego danej temperaturze powietrza w przypadku maksymalnej zawartości wilgoci w postaci pary. Temperatura powietrza ogranicza zawartość fazy parowej w powietrzu.

Stan pary wodnej zawartej w powietrzu w zależności od jej ilości może także ulegać zmianie; od pary przegrzanej przy ciśnieniu cząstkowym pary p_p < p_s, do pary nasyconej suchej przy ciśnieniu cząstkowym pary p_p = p_s odpowiadającym maksymalnej zawartości wilgoci w fazie gazowej. Nadmiar wilgoci ponad stan nasycenia może wystąpić tylko w fazie ciekłej lub stałej, a więc w postaci mgły ciekłej lub lodowej.

Ponieważ w powietrzu o danej temperaturze jest ograniczona zawartość wilgoci w postaci pary, można tę maksymalną zawartość wilgoci przyjąć jako wskaźnik porównawczy zawartości wilgoci w powietrzu niedosyconym. Na tej podstawie wprowadzono pojęcie stopnia nasycenia
, który stanowi stosunek aktualnej zawartości wilgoci w powietrzu x do zawartości wilgoci x” w stanie nasycenia przy temperaturze powietrza t

(5)

gdzie
jest maksymalną zawartością wilgoci w fazie gazowej w powietrzu o temperaturze t, której odpowiada ciśnienie nasycenia pary p_s. Stopień nasycenia
określa więc oddalenie aktualnego stanu powietrza od stanu jego nasycenia.

Istnieją jeszcze inne tradycyjne wskaźniki zawartości wilgoci w powietrzu wywodzące się z meteorologii jak: wilgotność bezwzględna (lub wilgoć gazu) oraz wilgotność względna (lub wprost wilgotność). Wilgotność bezwzględna oznacza masę pary wodnej zawartej w jednostce objętości powietrza wilgotnego. Ponieważ objętość roztworu jest taka sama jak objętość składników przy ich ciśnieniach cząstkowych, wilgotność bezwzględna jest więc równocześnie gęstością pary wodnej zawartej w gazie przy jej ciśnieniu cząstkowym i w temperaturze gazu wilgotnego (tj.
). Maksymalna wilgotność bezwzględna przy danej temperaturze powietrza wi1gotnego jest równa gęstości pary nasyconej suchej przy tej temperaturze, tj.
.

Wilgotność względna
jest stosunkiem rzeczywistej wilgotności bezwzględnej do maksymalnej przy tej samej temperaturze, a zatem

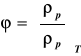
(6)

W przypadku dostatecznie małych ciśnień cząstkowych pary można jej gęstość wyrazić za pomocą równania Clapeyrona i wtedy

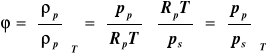
(7)

Wzór ten jest ważny, gdy p_s < p.

Jeśli składniki powietrza wilgotnego będą traktowane jako gazy doskonałe, to równania Clapeyrona dla gazu suchego i pary wodnej będą miały postać:

(8)

(9)

Po podzieleniu równań stronami otrzymuje się zależność

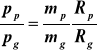
z której, po uwzględnieniu, że x = m_p/m_g i p_g = p - p_s, dochodzi się do wzoru

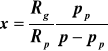
(10)

ważnego dla każdego gazu pod niskim ciśnieniem, zawilżonego parą dowolnej cieczy.

Dla powietrza zawilżonego parą wodną R_p = 461,5 J/kg K, R_g = 287.04 J/(kgK) i stosunek R_g/R_{p =} 0.622. Uwzględniając ponadto, że z równania (7) p_p = ϕp_s, otrzymuje się związek między zawartością wilgoci x i wilgotnością względną dla powietrza zawilżonego parą wodną:

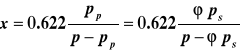
(11)

Z zależności tej można otrzymać po przekształceniach wzór określający ciśnienie cząstkowe pary wodnej w powietrzu wilgotnym o określonej zawartości wilgoci x i przy ciśnieniu powietrza p

(12)

Zawartość wilgoci w stanie nasycenia wyrazi się analogicznym wzorem jak (11), z tym, że zamiast ciśnienia p_p wystąpi ciśnienie nasycenia p_s, a zatem

(13)

Związek między wilgotnością względną
i stopniem nasycenia
można otrzymać podstawiając do równania definicyjnego stopnia nasycenia (5) x i
wyrażone wzorami (11) i (13), skąd

(14)

2. Równanie stanu powietrza wilgotnego

Przy niezbyt wysokich ciśnieniach gazy wilgotne stosują się do równania stanu Clapeyrona, które dla powietrza wilgotnego ma postać:

(15)

gdzie R oznacza stałą gazową gazu wilgotnego.

Stałą gazową R można obliczyć podstawiając do równania (4), wyrażającego prawo Daltona, ciśnienie gazu i wilgotnego obliczone z równania (15) i ciśnienia cząstkowe obliczone z równań (8) i (9)

skąd

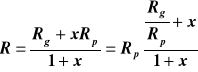
(16)

Dla powietrza zawilżonego parą wodną po uwzględnieniu R_g/R_p = 0.622 otrzymuje się

J/(kgK) (17)

1.3. Objętość właściwa i gęstość powietrza wilgotnego

Z równania Clapeyrona powietrza wilgotnego, zapisanego w postaci

(18)

można obliczyć objętość właściwą powietrza wilgotnego odniesioną do 1 kg gazu wilgotnego

(19)

a po uwzględnieniu stałej gazowej R wyrażonej wzorem (17)

(19a)

lub gęstość:

(20)

Ze wzoru (19a) wynika, że w warunkach tego samego ciśnienia i temperatury objętość właściwa gazu wilgotnego v jest większa od objętości właściwej powietrza suchego
(v dla x = 0), gdyż

Z równania (18) można również określić objętość właściwą powietrza wilgotnego, odniesioną do masy powietrza suchego zawartego w powietrzu wilgotnym m_g i objętość właściwa, którą oznacza się symbolem
będzie równa

(21)

a po uwzględnieniu R ze wzoru (17)

(21a)

jest objętością masy (1+x) kg gazu wilgotnego (na (1+x) kg). Jak wynika z porównania wzorów (19) i (21), między objętościami właściwymi v i
zachodzi związek

(22)

Uwzględniając ostatnią zależność, można obliczyć gęstość powietrza wilgotnego również ze wzoru

(23)

1.4. Entalpia i energia wewnętrzna powietrza wilgotnego

Obliczenia cieplne przemian gazu wilgotnego wymagają znajomości jego entalpii i energii wewnętrznej.

Entalpia gazu wilgotnego jest sumą entalpii gazu suchego i entalpii zawartej w gazie wilgoci, co można zapisać za pomocą równania

(24)

w którym i_g i i_p oznaczają entalpie właściwe gazu suchego i wilgoci zawartej w gazie wilgotnym (odniesione do 1 kg każdego z tych składników).

Obliczona z ostatniego równania entalpia właściwa gazu wilgotnego będzie równa:

(25)

Jako poziom odniesienia entalpii powietrza suchego przyjmuje się zwykle temperaturę 0°C, a więc w temperaturze tej entalpia powietrza suchego jest równa zero.

Przy takim założeniu entalpia powietrza jest funkcją temperatury powietrza wyrażonej w °C i można ją liczyć z zależności

(26)

w której

jest średnią właściwą pojemnością cieplną powietrza suchego przy stałym ciśnieniu.

W obliczeniach entalpii wilgoci przyjmuje się zwykle, że ciecz w temperaturze 0°C ma entalpię równą zero, w obliczeniach entalpii pary zawartej w powietrzu należy zatem uwzględnić ciepło parowania w temperaturze 0°C. Entalpia pary wodnej zawartej w powietrzu w temperaturze t jest wówczas równa

(27)

przy czym

jest średnią właściwą pojemnością cieplną pary wodnej przy stałym ciśnieniu, r₀ oznacza ciepło parowania wody w temperaturze 0°C.

Jeśli powietrze zawiera wilgoć nie tylko w fazie gazowej, ale również w fazie ciekłej lub stałej (mgły śnieżnej), to należy podczas obliczania entalpii takiego powietrza uwzględnić oddzielnie entalpię fazy gazowej i oddzielnie entalpię fazy ciekłej lub fazy stałej.

Powietrze o zawartości wilgoci x, zawierające oprócz pary wodnej mgłę wodną lub śnieżną, składa się z wilgoci w fazie parowej (pary nasyconej suchej) w ilości
(przy danej temperaturze powietrza) i wilgoci w fazie ciekłej lub stałej w ilości x -
.

Entalpia właściwa mgły wodnej jest równa

(28)

gdzie

- właściwa pojemność cieplna wody.

Entalpia mgły śnieżnej natomiast, która występuje w temperaturach niższych od 0°C, przy poprzednio przyjętych założeniach stanu odniesienia entalpii będzie równa

(29)

gdzie:

- ciepło krzepnięcia cieczy,

- właściwa pojemność cieplna lodu.

Zakładając, że właściwe pojemności cieplne pary wodnej i powietrza suchego mają stałe wartości równe średnim wartościom dla pary
= 1.926 kJ/(kgK), dla powietrza suchego
= 1.005 kJ/(kgK) oraz przyjmując ciepło parowania wody w temperaturze 0 °C
= 2500 kJ/kg, właściwą pojemność cieplną wody
= 4.19 kJ/(kgK), ciepło krzepnięcia wody
= 333,4 kJ/kg i właściwą pojemność cieplną 1odu
= 2,05 kJ/(kgK), otrzyma się po podstawieniu do (25) następujące wzory liczbowe do obliczania entalpii właściwej powietrza zawilżonego wodą:

- dla powietrza wilgotnego nie zawierającego mgły (o zawartości wilgoci x <
)

kJ/kg.p.s (30)

- dla powietrza zamglonego zawierającego tylko krople cieczy

kJ/kg.p.s (31)

lub po dokonaniu przekształceń

(31a)

- dla powietrza wilgotnego zawierającego mgłę śnieżną

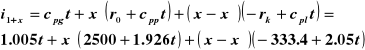
(32)

lub po przekształceniu

(32a)

Entalpię gazu wilgotnego o masie
oblicza się mnożąc entalpię właściwą --> [Author:F] gazu wilgotnego
przez masę gazu suchego, a więc

(33)

Energię wewnętrzną gazu wilgotnego oblicza się z równania Gibbsa i także odnosi się ją do (1+x) kg gazu wilgotnego, a zatem do ilości gazu zawierającego 1 kg gazu suchego, a więc

(34)

gdzie v jest objętością właściwą gazu wilgotnego (odniesioną do 1 kg gazu wilgotnego).

Energia wewnętrzna gazu wilgotnego o masie mg(1+x) jest równa

(35)

---