Labolatorium mechaniki płynów
Wydział Wiertnictwa Nafy i Gazu	Rok: II		Grupa I/1
Temat: Pomiary natężenia przepływu z wykorzystaniem rurki Pitota - Prandtla , zwężki Venturiego i kryzy.
Zespół w składzie: Konrad Stański Grzegorz Kurzeja Krystian Lubas Krystian Krauz		Data: 13-03-2004r.		Ocena:

1. Cel ćwiczenia.

Celem ćwiczenia było poznanie niektórych metod pomiaru strumienia objętości (objętościowego natężenia przepływu) i porównanie wyników uzyskanych przy zastosowaniu różnych metod i przyrządów.

Podczas ćwiczeń strumień objętości powietrza mierzyliśmy za pomocą dyszy Venturiego, kryzy oraz sondy spiętrzającej Prandtla.

2. Pomiar przy użyciu zwężki Venturiego.

Dysza Venturiego (zwężka) jest to przyrząd służący do pomiaru prędkości przepływu płynu (tj. gazu lub cieczy) na podstawie zjawiska spadku ciśnienia w cieczy wraz ze wzrostem jej prędkości. Zwężka Venturiego składa się z barometru różnicowego i rurki o zwężonym przepływie (właściwej dyszy). Jedna z końcówek barometru włączona jest przed zwężeniem, a druga w samej dyszy.

Korzystając z równania Bernoulliego i warunku ciągłości przepływu, można wykazać, że różnica ciśnień wskazywanych przez barometr jest proporcjonalna do kwadratu prędkości przepływu płynu V przed dyszą i wynosi:

(ρ/2)V²[(S²/s²) - 1]

gdzie: ρ - gęstość płynu,

S - pole przekroju przed dyszą,

s - pole przekroju w dyszy.

Objętość przepływającego płynu przez zwężkę wyznaczamy ze wzoru:

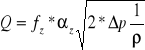
gdzie:
-objętościowe natężenie przepływu [m³/s]

-pole przekroju poprzecznego zwężki [m²]

-liczba przepływu dla zwężki

-przyrost ciśnienia [Pa]

-gęstość powietrza, współczynnik wyznaczany z tablic [kg/m³]

Współczynnik
wyznaczamy na podstawie zależności:

gdzie:
-temperatura na termometrze suchym [^oC]

-temperatura na termometrze mokrym [^oC]

-ciśnienie atmosferyczne [mmHg]

Różnicę ciśnień
mierzymy za pomocą mikromanometru .Zależność pomiedzy wychyleniem cieczy manometrycznej a różnicą ciśnień wyraża wzór:

gdzie:

-wysokość słupa cieczy [m], którą obliczymy z zależności:

-przyrost słupa cieczy w mikromanometrze,

sin  
-stała przyrządu,

-gęstość cieczy manometrycznej 800 [kg/m³]

g -stała grawitacji 9,81 [m/s²]

Pomiar przy użyciu kryzy ISA

Pomiar przy użyciu kryzy nie różni się od pomiarów dokonanych przy użyciu dyszy Venturiego. Różnica występuje tylko w budowie wewnętrznej .Kryza w przeciwieństwie do dyszy ,posiada ostre krawędzie pierścienia zwężającego strugę płynu. Obliczenia objętościowego natężenia przepływu oblicza się ze wzoru:

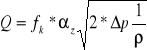
gdzie:
-objętościowe natężenie przepływu [m³/s]

-pole przekroju poprzecznego kryzy [m²]

-liczba przepływu kryzy

-przyrost ciśnienia [Pa]

-współczynnik wyznaczany z tablic [kg/m³]

Pomiar przy użyciu sondy spiętrzającej Prandtla

Sonda tego typu pozwala na pomiar różnicy ciśnienia statycznego i całkowitego. Różnica tych dwóch ciśnień jest ciśnieniem dynamicznym.

Obliczenia objętościowego natężenia przepływu . Dokonuje się na podstawie wzoru:

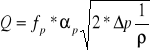
gdzie:
-objętościowe natężenie przepływu [m³/s]

-pole przekroju dla sondy [m²]

-liczba przepływu sondy

-przyrost ciśnienia [Pa]

-współczynnik wyznaczany z tablic [kg/m³]

Obliczenia:

Różnice ciśnień
wskazywane przez mikromanometry dla kolejnych natężeń przepływu dla kryzy, dyszy oraz rurki Prandtla odpowiednio wynoszą:

Lp	Różnica ciśnień dla kryzy p [Pa]	Różnica ciśnień dla zwężki p [Pa]	Różnica ciśnień dla rurki p [Pa]
1	160,884	84,7584	51,012
2	78,480	56,5056	23,544
3	39,240	28,2528	7,848
4	23,544	18,8352	3,924
5	62,784	45,5184	19,620
6	90,252	62,7840	27,468
7	313,920	210,3264	109,872
8	262,908	152,2512	51,012

Objętościowe natężenie przepływu obliczamy ze wzoru:

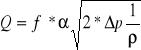
=0,0071 [m²]

=0,0088 [m²]

=0,0177 [m²]

=1,63 [kg/m³] dla
=21,9 (⁰C) ,
=13,1 (⁰C) ,
=739 (mmHg)

=1,120

=0,723

=0,800

Obliczenia natężenia przepływu dla ośmiu kolejnych pomiarów zostały przedstawione poniżej:

Lp	Natężenie przepływu dla kryzy Q[m^3/s]	Natężenie przepływu dla zwężki Q[m^3/s]	Natężenie przepływu dla rurki Q[m^3/s]
1	0,089	0,081	0,112
2	0,062	0,066	0,076
3	0,044	0,047	0,044
4	0,034	0,038	0,031
5	0,056	0,059	0,069
6	0,067	0,070	0,082
7	0,124	0,128	0,164
8	0,114	0,109	0,112

Liczbę Reynoldsa obliczamy ze wzoru:

gdzie: Re -liczba Reynoldsa

-średnia prędkość przepływu [m/s]

-lepkość kinematyczna powietrza 16*10^-6 [m²/s]

D -średnica przewodu 0,15 [m]

Obliczenia liczby Reynoldsa dla ośmiu kolejnych natężeń przepływu zostały przedstawione poniżej:

Lp	Wartość liczby Reynoldsa	Średnia prędkość przepływu płynu [m/s]
1	56250,0	6
2	42187,5	4,5
3	23437,5	2,5
4	10312,5	1,1
5	37500,0	4
6	46875,0	5
7	103125,0	11
8	84375,0	9

Na podstawie otrzymanych wyników został sporządzony wykres przedstawiający zależność liczby Reynoldsa od objętościowego natężenia przepływu.

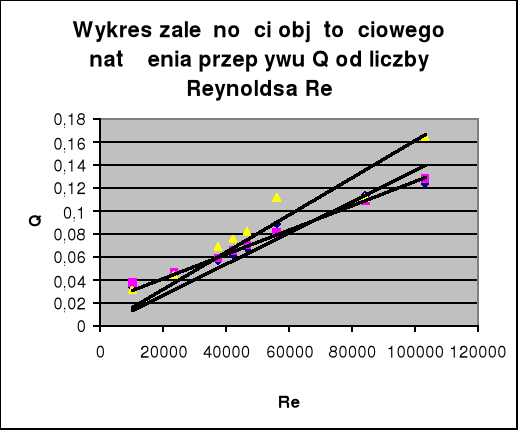
Wnioski:

Dokonane pomiary objętościowego natężenia przepływu trzema różnymi przyrządami różnią się nieznacznie od siebie .Wynika to z błędu paralaksy popełnionego przy odczytywaniu wyników. Dodatkowa należy wziąć pod uwagę inne czynniki, które wpłynęły na rezultat pomiaru takie np. jak niedokładność przyrządu pomiarowego, straty powstałe przy przepływie płynu oraz inne czynniki zewnętrzne, które nie zostały uwzględnione.

---