O pewnych problemach przekształcania wartości cech

Bolesław Borkowski, Hanna Dudek, Wiesław Szczesny

Katedra Ekonometrii i Informatyki

SGGW w Warszawie

Ul. Nowoursynowska 159

02-787 Warszawa

Abstract

The article presents the problem of the influence of normalization of diagnostic variables on linear ordering of objects. In the authors' opinion, transformations of diagnostic variables should not change arrangement of objects determined by latent variable.

It is found that the results of linear ordering of objects depend on the selection of normalization method. The best result is obtained by using quotient transformation with formula X^* = F^-1[1- F(X)] turning the destimulant into stimulant. Moreover, it is found that using information about weighs of diagnostic variables improves quality of linear ordering of objects.

Key words: normalization method, latent variable, arrangement of objects.

Słowa kluczowe: metoda normalizacji, cecha ukryta, uporządkowanie obiektów.

1. Wstęp

W badaniach ekonomicznych często wykorzystuje się wielowymiarową analizę danych. Najogólniej polega ona na opisie zjawiska przy uwzględnianiu wielu cech (Borkowski, Szczesny 2002). Cechy te wyrażane są w różnych jednostkach miary oraz odpowiadają im zróżnicowane obszary zmienności (Zeliaś 2000). Bezpośrednie porównywanie takich cech jest bardzo utrudnione a czasami wręcz niemożliwe. W literaturze przedmiotu (Gatnar, Walesiak 2004, Ostasiewicz 1999) podaje się wiele metod normowania. Metody te polegają na przekształceniach, w wyniku których otrzymuje się tzw. zmienne transformowane. Zmienne te charakteryzują się potencjalnie jednakowym zakresem zmienności oraz pozbawione są miana. Spośród wielu metod, do najpopularniejszych należą metody standaryzacji, unitaryzacji, przekształceń ilorazowych oraz metody rangowe. Sposób wykorzystania tych metod oraz ich wady i zalety omówione zostały w sposób profesjonalny przez Prof. Kukułę (Kukuła 2000). Przy wyborze najlepszej metody, Autor na podstawie badań symulacyjnych, poleca te metody przekształceń, które dawały wyniki najbliższe pozostałym metodom normowania.

W artykule chcemy rozszerzyć tę analizę o dodatkową własność. Mianowicie uważamy, że przekształcenia cech nie powinny zmieniać lub minimalnie zmieniać porządkowanie zadane przez cechę ukrytą i nie powinny wpływać na zmianę koncentracji wartości cechy porządkującej.

2. Metoda

Dla większej przejrzystości badań wybraliśmy przykład z cechami, które są symulantami i destymulantami a cechą ukrytą jest liniowa funkcja tych cech. Rozpatrzyliśmy zbiór zawierający 6 cech, w tym 3 z nich są stymulantami i 3 destymulantami. Cechami będącymi symulantami są kategorie dochodowe a destymulantami - kategorie kosztowe. Cechą ukrytą jest wynik finansowy określony jako różnica między kosztami a dochodami. Wiemy o tym, że w praktyce cecha ukryta występuje rzadko w postaci znanej funkcji cech obserwowanych. Macierz korelacji i wykresy korelacyjne badanych cech wskazuje na silna zależność pomiędzy cechami a cecha ukrytą oraz pomiędzy poszczególnymi cechami występuje zależność nieliniowa (por. rys.1).

Rysunek 1. Macierz współczynników korelacji i wykresów korelacyjnych

Picture 1. Matrix of correlation coefficients and scatterplot matrix

Źródło: Obliczenia własne

3. Analiza wyników

W pierwszej kolejności wygenerowaliśmy wartości cech oraz obliczyliśmy wartości porządkującej cechy ukrytej dla 25 obiektów . Wartości te przedstawia tab.1.

Tabela 1.Wartości badanych cech

Table 1. Values of diagnostic variables

Źródło: Obliczenia własne

Przyjęliśmy, że cechy te odnoszą się do oddziałów pewnego banku, gdzie D1 - D3 są to dochody poszczególnych dziedzin działalności z uwzględnieniem kosztów transferu funduszy, K1 - K3 to kategorie kosztów działalności a W - wynik ekonomiczny (finansowy) oddziału. W działalności banku często występuje konieczność oceny oddziałów względem ich efektywności działania. Jest to zagadnienie bardziej skomplikowane, ponieważ opiera się na wielu miernikach efektywności. W naszym uproszczony przykładzie takie uszeregowanie oddziałów jest równoznaczne z ustawieniem według wartości wyniku ekonomicznego (por. tab. 1). Z reguły wartości ukrytej cechy (porządkującej według efektywności działalności oddziałów banku) są nieznane. Dlatego też do rozwiązania tego problemu wykorzystuje się cechy, których wartości są zależne od cechy ukrytej. Do rozwiązania tego problemu wykorzystywane są różne metody tworzenia cechy, według której dokonuje się porządkowania. Metody te polegają na sumowaniu odpowiednio unormowanych cech. W badaniach wykorzystaliśmy metody powszechnie stosowane: metody rangowe, standaryzacji i unitaryzacji oraz inne przekształcenia ilorazowe. Naturalną metodą jest proste porządkowanie według sumy rang (por. tab.2).

Tabela 2. Kolejność poszczególnych oddziałów według metody rangowej

Table 2. Arrangement of branches obtained via rank method

Źródło: Obliczenia własne

Powszechnie wiadomo, że metoda ta pomimo swojej prostoty, ma poważną ułomność, ponieważ zachowuje tylko porządek wartości poszczególnych cech a zatem zniekształca odległości pomiędzy wartościami cechy ukrytej, jeżeli mierzona ona jest na innej skali niż porządkowa. Z analizy danych tej tabeli wynika, że uszeregowanie oddziałów (kolumna „pozycja”) zostało znacznie zmienione w porównaniu do poprzedniego uporządkowania (por. tab. 1, kolumna W).

W następnej kolejności do uszeregowania oddziałów wykorzystaliśmy metodę unitaryzacji. Przekształcenia cech dokonaliśmy według następujących formuł:

a) dla stymulanty: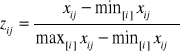

b) dla destymulanty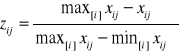

Po przekształceniu cech otrzymaliśmy uszeregowanie oddziałów (por. tab. 3).

Tabela 3. Kolejność poszczególnych oddziałów według unitaryzacji zerowanej

Table 3. Arrangement of branches obtained via unitarisation method

Źródło: Obliczenia własne

Na podstawie uzyskanych wyników zawartych w tab.1 - 3 można stwierdzić, że zgodnie z analizą przeprowadzoną wcześniej przez Prof. K. Kukułę otrzymaliśmy inne uszeregowania stosując różne metody. Oczywiście, uszeregowanie uzyskane poprzez przekształcenie cech metodą unitaryzacji zerowanej jest lepsze niż uzyskane metodą rangową.

W dalszym kroku analizy wykorzystaliśmy metodę standaryzacji do przekształcanie wartości cech (odpowiednio
). Wyniki obliczeń zamieściliśmy w tab. 4, w której kolumna „pozycja” opisuje kolejność oddziałów.

Tabela 4. Kolejność poszczególnych oddziałów według standaryzacji

Table 4. Arrangement of branches obtained by using standardization

Źródło: Obliczenia własne

W tym przypadku kolejność oddziałów jest prawie taka sama jak wskazuje na nią wartość cechy ukrytej. Jedynym odstępstwem (bardzo poważnym) jest umieszczenie na poz. 13 oddziału najgorszego pod względem wielkości wyniku finansowego.

W ostatni etapie dokonaliśmy uporządkowania oddziałów wykorzystując metodę przekształcenia ilorazowego dla stymulanty i destymulanty zastosowaliśmy odpowiednio formuły:
) (Strahl, Walesiak 1997).

Tabela 5. Kolejność poszczególnych oddziałów według przekształceń ilorazowych wykorzystujących średnia arytmetyczną

Table 5. Arrangement of branches obtained via quotient transformation using the arithmetic mean

Źródło: Obliczenia własne

Metodą przekształcenia ilorazowego uzyskaliśmy nieznacznie gorsze wyniki w porównaniu do wyników uzyskanych w przypadku standaryzacji. Zauważalnym odstępstwem pozostał oddział 25 o najgorszym wyniku, który został sklasyfikowany na 14 pozycji (por. kol. „pozycja”). Przeprowadzona analiza wykazała, że żadna z wykorzystanych metod przekształceń cech nie dała uporządkowania zgodnego z porządkiem zadanych przez cechę ukrytą.

Cechy przyjęte w badaniu charakteryzują się tym, że ich wartości mierzone są na tej samej skali. Wobec tego nie wymagają one przekształceń normujących. Problemem do rozwiązania jest zmiana stymulanty na destymulanty. Powszechnie wykorzystywane są tu funkcje malejące. Jednakże problem stanowi nie tylko wybór postaci tej funkcji, ale także postulatów jakie powinna spełniać ta funkcja. Głównym postulatem takiej zmiany powinno być według naszej oceny zachowanie identycznego rozkładu zmiennej X z rozkładem zmiennej przekształconej X* mającej „przeciwny zwrot”. Stosowane powszechnie przekształcenia stymulanty na destymulanty nie spełniają tego postulatu. W takich przypadkach proponujemy wykorzystanie formuły X^* = F^-1[1- F(X)], gdzie F oznacza dystrybuantę zmiennej X (Conti, 1993). Powyższe przekształcenie wykorzystaliśmy w naszym przykładzie (por. tab.6).

Tabela 6. Przekształcenie destymulant według formuły X^* = F^-1[1- F(X)]

Table 6. Transformation of destimulants by X^* = F^-1[1- F(X)] formula

Źródło: Obliczenia własne

Wykorzystanie tej formuły do przekształcenia destymulanty dało uporządkowanie zgodne z uporządkowaniem zadanym przez cechę ukrytą. W prezentowanym przykładzie wszystkie cechy były na jednakowej skali, wobec tego nie wymagały normowania. W tym przypadku możemy w prosty sposób policzyć wagi tych cech (np. poprzez % udział w sumie wartości poszczególnych cech). Obliczone wagi możemy odnieść do cech po przekształceniu (Walesiak 2005). Wydaje się, że taki zabieg powinien przywrócić właściwe uporządkowanie obiektów (zgodne z uporządkowaniem zadanym przez cechę ukrytą). Wyniki takiej operacji zastosowaliśmy do rozpatrywanych 5 metod przekształceń wartości cech (tab. 7). Z analizy danych zamieszczonych w tabeli 7 wynika, że właściwe uporządkowanie obiektów, zgodne z uporządkowaniem zadanym przez cechę ukrytą uzyskaliśmy wykorzystując przekształcenie ilorazowe wykorzystujące średnią arytmetyczną z proponowanym przekształceniem destymulanty według formuły X^* = F^-1[1- F(X)]. Oczywiście zastosowanie wag poprawiło wszystkie rozpatrywane uporządkowania, jednak nie doprowadziły do uporządkowania zgodnego z tym według cechy ukrytej. Nie oznacza to, że w każdym przypadku uzyskamy zawsze najlepsze wyniki stosując niniejszą metodę. Nie mniej jednak rozpatrywany problem wart jest dalszej pogłębionej analizy na danych o innej strukturze informacyjnej.

Tabela 7. Ważone wartości sumy przekształconych cech oraz pozycja oddziału w rankingu

Table 7. Weighted values of sums of transformed variables and position of branches in ranking

Źródło: Obliczenia własne, gdzie: Suma il* oznacza zmienna ważoną według przekształcenie ilorazowego z zamianą destymulanty według formuły X^* = F^-1 [1- F(X)]

Podsumowanie

Przeprowadzona analiza potwierdziła wnioski zawarte w opracowaniu Prof. K. Kukuły a mianowicie, że uzyskany porządek zależy od zastosowania metody normowania cech. W badaniu posłużyliśmy się przykładem, w którym cecha ukryta była znana. W tym przypadku najlepszą metodą normowania okazała się metoda ilorazowa, w której wykorzystaliśmy formułę X^* = F^-1 [1- F(X)] do zamiany destymulanty na stymulantę. Zastosowanie tej formuły przy przekształceniu zapewniło, że rozkład wartości stymulanty X^* jest identyczny z rozkładem destymulanty X. Przeprowadzone badania wskazały, że wykorzystanie informacji o znaczeniu poszczególnych cech (wagi) przy budowie cechy agregatowej poprawiło jakość uporządkowania.

Bibliografia

1. Borkowski B., Szczesny W. (2002): Metody taksonomiczne w badaniach przestrzennego zróżnicowania rolnictwa. Roczniki Nauk Rolniczych. Seria G -  Ekonomika Rolnictwa, t. 89, zeszyt 2, s. 11 -21.

2. Conti P. L. (1993): On some descriptive aspects of measures of monotone dependence. Metron. Vol. LI, No. 3-4, s. 43-60.

3. Gatnar E., Walesiak M. (2004): Metody statystycznej analizy wielowymiarowej w badaniach marketingowych. Wydawnictwo Akademii Ekonomicznej im O. Lanego we Wrocławiu, Wrocław.

4. Kukuła K. (2000): Metoda unitaryzacji zerowanej. Wydawnictwo Naukowe PWN, Warszawa.

5. Ostasiewicz W. (red.) (1999): Statystyczne metody analizy danych. Wydawnictwo Akademii Ekonomicznej im O. Lanego we Wrocławiu, Wrocław.

6. Strahl D., Walesiak M. (1997): Normalizacja zmiennych w skali przedziałowej i ilorazowej w referencyjnym systemie granicznym. Przegląd Statystyczny. Zeszyt 1, s. 69 - 77.

7. Walesiak M. (2005): Problemy selekcji i ważenia zmiennych w zagadnieniu klasyfikacji. Taksonomia 12. Klasyfikacja i analiza danych - teoria i zastosowania. Prace Naukowe Akademii Ekonomicznej im Oskara Lanego we Wrocławiu, Wrocław.

8. Zeliaś A. (2002): Some Notes on the Selection of Normalization of Diagnostic Variables, Statistics in Transition. Vol. 5, No. 5, s. 787-802.

Afiliacja autorów:

Katedra Ekonometrii i Informatyki

SGGW w Warszawie

Streszczenie

W pracy podjęto temat wpływu metody normalizacji cech na uporządkowanie obiektów. Zdaniem autorów przekształcenia cech nie powinny zasadniczo zmieniać porządkowania zadanego przez cechę ukrytą i nie powinny wpływać na zmianę koncentracji wartości cechy porządkującej.

Na wygenerowanym przykładzie przeanalizowano wyniki uzyskane metodą standaryzacji, unitaryzacji, przekształceń ilorazowych oraz metodami rangowymi. Przeprowadzona analiza potwierdziła wnioski zawarte w pracy Prof. Kukuły a mianowicie, że uzyskany porządek zależy od zastosowania metody normowania cech. W badaniu posłużono się przykładem, w którym cecha ukryta była znana. W tym przypadku najlepszą metodą normowania okazała się metoda ilorazowa, w której wykorzystano formułę X^* = F^-1[1- F(X)] do zamiany destymulanty na stymulantę. Zastosowanie tej formuły przy przekształceniu zapewniło, że rozkład wartości stymulanty X^* jest identyczny z rozkładem destymulanty X. Przeprowadzone badania wykazały, że wykorzystanie informacji o wagach poszczególnych cech przy budowie cechy agregatowej poprawiło jakość uporządkowania.

About problems of transformation of diagnostic variables

Summary

The article presents the problem of the influence of normalization of diagnostic variables on linear ordering of objects. The considered methods are: rank method, unitarization, standardization and quotient transformation. In the authors' opinion, transformations of diagnostic variables should not change arrangement of objects determined by latent variable.

The analysis is carried out on artificial data. The diagnostic variables (three stimulants and three destimulants) describe financial results of 25 branches of the bank. It is found that the results of linear ordering of objects depend on the selection of normalization method. The best result is obtained by using quotient transformation with formula X^* = F^-1[1- F(X)] turning the destimulant into stimulant. Moreover, it is found that using information about weighs of diagnostic variables improves quality of linear ordering of objects.

11

---