Nr ćwicz. 108	Data: 28.11.12	Kamil Sapikowski	Wydział BMiZ	Semestr: I	Grupa: 5 Lab: 6
prowadzący: mgr inż. Adrian Adamski			Przygotowanie:	Wykonanie:	Ocena ostat.:

Temat: Wyznaczanie modułu Younga metodą ugięcia.

Wstęp teoretyczny:

Gdy na pręt podłużny działa siła prostopadle do jego długości, doznaje on ugięcia, a wielkość tzw. strzałki ugięcia S (rys. 1.) jest zawsze proporcjonalna do siły F, a także zależy od wymiarów geometrycznych, sposobu mocowania pręta i rodzaju materiału z którego jest on wykonany.

Rys. 2. Element pręta zgiętego

Rys. 1. Ugięcie pręta

Zgodnie z prawem Hooke'a wydłużenie jest proporcjonalne do siły i długości początkowej oraz odwrotnie proporcjonalne do powierzchni przekroju

gdzie: E - moduł Younga,
- siła rozciągająca badaną warstwę elementarną.

Taka sama siła, lecz przeciwnie skierowana, działa na warstwę elementarną położoną symetrycznie poniżej warstwy neutralnej N. Moment siły
względem warstwy N wynosi

Całkowity moment M sił działających na wszystkie warstwy zawarte między przekrojami 1 i 2 obliczam całkując powyższe równanie względem y po całej grubości

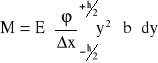
(1)

Jeśli oznaczę

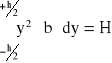
(2)

to równanie (1) mogę napisać w postaci

(3)

Równanie to otrzymałem rozpatrując odkształcenie pręta, którego bezpośrednią przyczyną jest siła F przyłożona do jego końca. Moment tej siły względem przekroju 2 wynosi
lub zaniedbując wielkość
jako małą w porównaniu z x

(4)

Kąt
jest zawarty między stycznymi do pręta w punktach, gdzie przekroje 1 i 2 przecinają górną powierzchnię. Na podstawie rysunku mogę napisać następujący związek

Wstawiając powyższe równanie do wzoru (3) i porównując wzory (3) i (4) otrzymuję elementarną strzałkę ugięcia

Całkowitą strzałkę ugięcia otrzymuję całkując powyższe równanie po całej długości pręta

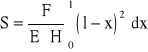
Po scałkowaniu, wyrażenie na całkowitą strzałkę ugięcia przyjmuje postać

Wartość współczynnika H zależy od kształtu i rozmiarów geometrycznych pręta. Gdy przekrój jest prostokątem o wysokości h i szerokości b, to całkowanie równania (2) prowadzi do wyniku

Całkowanie podobnego wyrażenia dla przekroju kołowego daje

Podstawiając wartości współczynników H otrzymuję odpowiednio dla obu przekrojów strzałki ugięcia

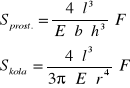
Otrzymane powyżej wzory odnoszą się do pręta jednostronnie obciążonego i jednym końcem umocowanego. Równania te można łatwo dostosować do sytuacji, gdy pręt jest swobodnie oparty dwoma końcami i obciążony w środku. Zachowuje się on wtedy tak, jak gdyby był zamocowany w środku, a na jego końce działały siły
skierowane ku górze. Siła
działa wtedy na pręt o długości
.

Po uwzględnieniu tych warunków w poprzednich wzorach uzyskuję wzory na strzałki ugięcia prętów

Rys. 3. Ugięcie pręta

dwustronnie podpartych

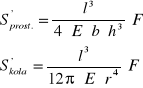
Z powyższych wzorów obliczam moduł Younga dla przekroju prostokątnego:

(5) i dla przekroju kołowego:
(6)

Tabela pomiarowa:

Pręt 1 Pręt 2

ho = 608,81 ho = 610,28

Lp.	obciążenie [g]	wysokość h [mm]	strzałka s [mm]
1.	190	609,39	0,89
2.	380	608,50	1,78
3.	850	606,65	3,63
4.	1320	604,77	5,51
5.	1790	602,91	7,37

Lp.	obciążenie [g]	wysokość h [mm]	strzałka s [mm]
1.	190	607,93	0,88
2.	380	607,45	1,36
3.	850	605,96	2,85
4.	1320	604,78	4,03
5.	1790	603,19	5,62

Pręt 3 Pręt 4

ho = 606,91 ho = 610,47

Lp.	obciążenie [g]	wysokość h [mm]	strzałka s [mm]
1.	190	606,51	0,4
2.	380	605,61	1,3
3.	850	604,54	2,37
4.	1320	603,35	3,56
5.	1790	602,28	4,63

Lp.	obciążenie [g]	wysokość h [mm]	strzałka s [mm]
1.	190	610,17	0,3
2.	380	609,43	1,04
3.	850	608,80	1,67
4.	1320	607,90	2,57
5.	1790	607,43	3,04

---