Niezbędny zakres tematyczny obowiązujący do przygotowania się do zajęć:

1.Obiekt dynamiczny ciągły i liniowy:

• obiekty ciągłe - T=R, gdzie R - zbiór liczb rzeczywistych (czas jest zmienną ciągłą)

• obiekty liniowe - obiekty, których opis ma postać zależności liniowych. Musi więc być spełniona zasada superpozycji. Nie mogą występować żadne operacje nieliniowe na zmiennych układu, a parametry układu nie mogą zależeć od zmiennych.

W większości przypadków punktem wyjścia do oceny własności dynamicznych układów liniowych jest liniowe równanie różniczkowe. Równanie powstaje na podstawie analizy i opisu zjawisk fizycznych charakteryzujących dany układ.
Postać ogólna takiego równania jest następująca:

2.Transmitancja operatorowa i widmowa:

• Transmitancja widmowa to w automatyce stosunek wartości zespolonej odpowiedzi Y układu wywołanej wymuszeniem sinusoidalnym, do wartości zespolonej tego wymuszenia, w stanie ustalonym. Transmitancja widmowa opisuje odtwarzanie przez dany obiekt (układ) zmieniającego się sygnału wejściowego i można otrzymać ją przechodząc z transmitancji operatorowej przez podstawienie s = jω.

• Transmitancja operatorowa - stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego układu przy zerowych warunkach początkowych:

3.Moduł transmitancji:

Moduł transmitancji opisuje wzmocnienie układu:

  
A_wy-amplituda wyjściowa, A_we-amplituda wejścia

4.Kąt przesunięcia fazowego:

Kąt przesunięcia fazowego jest to różnica pomiędzy wartościami fazy dwóch okresowych ruchów drgających . (a także pytanie 12)

5.Podstawowe człony dynamiczne

a). Człon proporcjonalny (bezinercyjny)

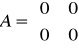
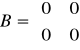
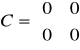
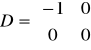
transmitancja: G(s) =kp

przykładowe równanie ma postać: y=kp*u

b). Człon całkujący

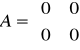
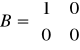
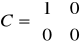
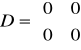
transmitancja: G(s)=kr/s

przykładowe równania układu mają postać: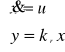

c). Człon inercyjny.

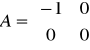
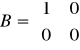
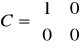
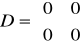
transmitancja: G(s)=kp/(T*s+1)

przykładowe równania układu mają postać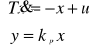

d). Człon różniczkujący rzeczywisty

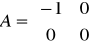
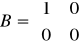
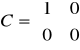
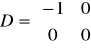
Przykł. równania układu mają postać: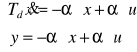

e). Człon dwuinercyjny

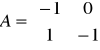
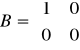
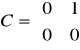
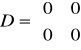
Przykł. równania układu mają postać: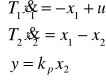

f). Człon proporcjonalno całkujący

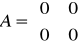
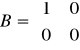
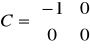
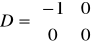
Przykł. równania układu mają postać: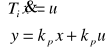

g). Człon oscylacyjny

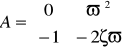
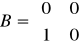
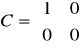
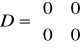
ξ-tłumienie (decyduje o char. oscylacji); ω-częstość x₁,x₂-zmienne fazowe

Przykł. równania układu mają postać: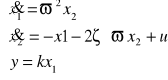

6.Obserwowalność:

Obserwowalność - na podstawie przebiegu sygnału wyjściowego w skończonym przedziale czasu, można określić stan układu w dowolnej chwili tego przedziału.

Układ jest obserwowalny (całkowicie) - jeśli przy danym dowolnym sterowaniu U(t), istnieje skończona chwila t_k, po której, na podstawie znajomości wektora sygnałów wyjściowych Y(t) i wektora sterowania U(t) w przedziale od t₀ do t_k można wyznaczyć stan układu X(t₀) w dowolnej chwili początkowej t₀.

Sens pojęcia sprowadza się do tego czy poszczególne zmienne stanu wpływają na wyjście w sposób na tyle niezależny od siebie że umożliwia to odróżnienie ich wpływu
w zaobserwowanym przebiegu y.

Warunek obserwowalności: warunkiem koniecznym i dostatecznym (wystarczającym) obserwowalności jest, aby macierz:

o wymiarach m x n miała rząd n, czyli zawierała n - liniowo niezależnych wierszy.

Dla ułatwienia analizy macierzy O, wprowadza się macierz W, która jest transpozycją macierzy O. Warunek obserwowalności odnoszący się do macierzy W formułuje się następująco: układ jest całkowicie obserwowalny wtedy i tylko wtedy, gdy rząd macierzy
jest równy n.

Warunek:

7.Sterowalność:

Sterowalność - możliwość osiągnięcia dowolnego stanu układu w skończonym czasie za pomocą dopuszczalnego sterowania (ograniczonego przedziałami i ciągłego)

Układ jest sterowalny (całkowicie) - gdy ograniczone przedziałami ciągłe sterowanie U(t) przeprowadza układ z dowolnego stanu początkowego X(t₀) w chwili t=t₀ do dowolnego stanu końcowego X(t_k) w chwili t=t_k w skończonym przedziale czasu
t_k-t₀>0.

Istotą tej własności jest fakt, że każda ze zmiennych stanu układu sterowanego powinna zależeć od sterowania w nieco inny sposób tak aby sterowanie nie powodowało identycznych zmian poszczególnych współrzędnych stanu.

Warunek sterowalności: warunkiem koniecznym i dostatecznym (wystarczającym) sterowalności jest, aby macierz

o n - wierszach i m - kolumnach miała rząd n, czyli n - liniowo niezależnych kolumn.

Warunek:

8.Stabilność:

Stabilność (układu liniowego) - to taki układ, którego rozwiązanie swobodne
(przy niezerowych warunkach początkowych) pozostaje ograniczone w dowolnym czasie.

Jest to równoważne temu, że: przy wymuszeniu ograniczonym co do wartości i czasu trwania odpowiedź układu była również ograniczona.

Stabilność asymptotyczna - oznacza, że układ jest nie tylko stabilny, a więc jego rozwiązania są ograniczone, ale przy czasie dążącym do nieskończoności rozwiązanie dąży do zera. Odpowiada to żądaniu aby rozwiązanie wymuszone było ograniczone nawet przy wymuszeniu (ograniczonym) trwającym dowolnie długo.

Układ stabilny globalnie - (o równaniu X'=Ax) wtedy i tylko wtedy gdy wszystkie wartości własne macierzy A mają niedodatnie części rzeczywiste i każda wartość własna o zerowej części rzeczywistej jest pierwiastkiem jednorodnym wielomianu.

Stabilność punktu równowagi przy dowolnie dużych warunkach początkowych nazywa się globalną.

Układ stabilny lokalnie - rozumiemy stabilność tylko w punkcie równowagi bez określenia zakresu sygnałów zaburzających, po ustąpieniu których układ wraca do równowagi.

Mówiąc o stabilności globalnej określamy jednocześnie obszar sygnałów zaburzających, po przejściu których układ zachowuje swój pierwotny stan równowagi. Jeżeli obszar stabilności globalnej obejmuje wszystkie możliwe sygnały wejściowe - stabilność lokalna.

Stabilność układu sprawdzamy na podstawie równania charakterystycznego układu. Wszystkie człony równania charakterystycznego muszą mieć wartość dodatnią.

Aby wyznaczyć równanie charakterystyczne układu należy obliczyć wyznacznik
z następującej zależności:

gdzie: I - macierz jednostkowa;

A - macierz stanu;

Kryteria stabilności:

- analityczne (Hurwitza, Roughta)

- graficzne (Nequista)

- anal-graf (Michałowa)

9.Równanie charakterystyczne i wielomian charakterystyczny:

Równanie charakterystyczne-równanie, powstające w wyniku przyrównania mianownika transmitancji operatorowej do zera. Służy do sprawdzenia stabilności układu. Wszystkie człony równania charakterystycznego muszą mieć wartość dodatnią.

Aby wyznaczyć równanie charakterystyczne układu należy obliczyć wyznacznik
z następującej zależności:

gdzie: I - macierz jednostkowa;

A - macierz stanu;

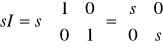
Wielomian charakterystyczny jest przypisywany w algebrze liniowej każdej macierzy kwadratowej. Zawiera informacje o niektórych własnościach tej macierzy, w szczególności jej wartościach własnych, wyznaczniku, i śladzie. Dla dowolnego ciała K możemy rozważać macierze n×n nad tym ciałem. Wielomian charakterystyczny takiej macierzy A, oznaczany przez pA(t), definiuje się jako

pA(t) = det( t I − A )

10.Stała czasowa w podstawowych członach dynamicznych:

T - w układzie automatyki, miara osiągania stanu ustalonego przez sygnał wyjściowy, związana z czasem trwania stanu nieustalonego następującego po zmianie sygnału wejściowego.

11.Charakterystyki układów dynamicznych:

Charakterystyka skokowa - odpowiedź na skokową zmianę sygnału wejściowego
o unormowanej amplitudzie. Odzwierciedla charakter danego obiektu.

Charakterystyka częstotliwościowa - określa zachowanie się układu przy wszystkich częstotliwościach wymuszenia, podając stosunek amplitud odpowiedzi do wymuszenia oraz przesunięcie fazowe między odpowiedzią, a wymuszeniem jako funkcję częstotliwości. Podstawę charakterystyk stanowi transmitancja widmowa.

12.Obliczanie modułu transmitancji i przesunięcia fazowego:

Moduł transmitancji:

A_wy-amplituda wyjściowa, A_we-amplituda wejścia

Przesunięcie fazowe między dwoma przebiegami okresowymi można określić jako

różnicę faz obu przebiegów w chwili ich przejścia przez określony, najczęściej zerowy

poziom :

ϕ = φ 1 - φ 2

Przesunięcie można wyrazić również proporcjonalnym przesunięciem czasowym (wyrażonym w mierze kątowej), jako stosunek różnicy czasów ∆ t momentów przejścia przebiegów przez zero, do okresu przebiegu T :

ϕ =2 Π ∆t/ T

13.Równania wektorowo-macierzowe układu dynamicznego:

- równanie stanu

- równanie wyjścia

14.Macierze: stanu, wejścia i wyjścia:

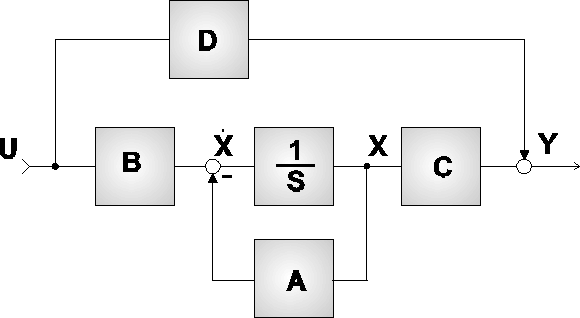
gdzie:

X(t) - wektor stanu

Y(t) - wektor sygnałów wyjściowych

U(t) - wektor sygnałów wejściowych

A - macierz stanu

B - macierz wejść (wpływ sygnału wejściowego na stan automatyki)

C - macierz wyjść (relacje między stanem wyjść, a stanem układu)

D - macierz transmisyjna układu (zależność między wejściem, a wyjściem)

Zastosowanie macierzy równań stanu:

Z analizy członów oscylacyjnych, można wywnioskować, że kolejne elementy macierzy A powodują (przy zwiększaniu ich wartości):

a₁₁-zwiększa amplitudę odpowiedzi

a₁₂-powoduje oscylacje

a₂₁-tłumi wykres odpowiedzi do zera

a₂₂-tłumi oscylacje

Macierz D powoduje zaś, że odpowiedź na wymuszenie w czasie t=0 osiąga wartość wymuszenia i dalej maleje lub rośnie zależnie od charakteru członu.

cw. 1 przekazniki
zasada dzialania, budowa, do czego sluzy, w jaki sposob i kiedy zestyki sie zwieraja i rozwieraja, wszystkie czasy, co to jest czas zestyku
ogolnie przejebka :]

ćw. 1:
- co to przekaźnik, zasada działania, jak jest zbudowany, gdzie się stosuje, jakie zalety;
- wszystkie czasy przełączeń, i jak je wyznaczamy;
- co to współczynnik kp;

cw 1
A) wspolczynnik zapasu B) prad znamionowy

jak zmieniaja sie czasy przekaznika gdy do cewki podlaczymy szeregowo rezystor

1. Porównać metody eliminowania drgań zestyków.
2. "Zakłócenia pracy przekaźnika" i metody ich eliminacji.

1. Porównać metody eliminowania drgań zestyków.
2. Z badanego na zajęciach układu ( UCY 7493) zbudować najprostszą metodą licznik mod 8.

2. Zakłócenia pracy przekaźnika i metody ich eliminacji.

7

---