Wyznaczenie obciążenia krytycznego pręta ściskanego metodą Southwella.

1. Cel ćwiczenia.

Celem ćwiczenia laboratoryjnego było wyznaczenie metodą Southwella obciążenia krytycznego sprężystego wyboczenia giętnego osiowo ściskanego pręta o cieńkościennym przekroju otwartym podpartego przegubowo na obu końcach.

2. Wstęp teoretyczny.

Wyboczenie sprężyste bisymetrycznego pręta jednoprzęsłowego o stałym przekroju sienkościennym i dowolnych warunkach podparcia, ściskanego osiowo siłą P, opisuje układ równań :

EI_xy^IV + P_y^II = 0

EI_yx^IV + P_x^II = 0

EI_ωϕ^IV + (Pi_o² - GI_s) ϕ^II = 0

gdzie:

x,y,ϕ - przemieszczenia liniowe wzdłuż osi x, y oraz kątowe w płaszczyźnie xy (skręcenie wokół osi z ),

x^II , x^IV , y^II , y^IV , ϕ^II , ϕ^IV - drugie i czwarte pochodne wymienionych przemieszczeń obliczone względem zmiennej z ,

i_o­ - biegunowy moment bezwładności względem środka ciężkości przekroju

E, G - moduły sprężystości podłużnej i poprzecznej

I_x , I_y , I_ω , I_s - momenty bezwładności względem osi x , y , wycinkowy i czystego skręcania.

Rozwiązując ten układ równań można wyznaczyć trzy wzajemnie niezależne składowe obciążenia : P_x ,P_y , Pϕ

1. siła krytyczna wyboczenia giętnego w płaszczyźnie yz

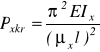
2. siła krytyczna wyboczenia giętnego w płaszczyźnie xz

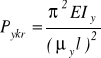
3. siła krytyczna wyboczenia skrętnego

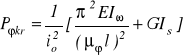
gdzie : l - długość teoretyczna pręta

μ - współczynniki długości wyboczeniowej przy wyboczeniu giętnym oraz skrętnym.

w naszym przypadku przy przegubowym podparciu obu końców pręta μ = 1,0 .

Doświadczalne wyznaczenie obciążenia krytycznego wyboczenia giętnego przeprowadzamy za pomocą metody Southwella. W metodzie tej wykorzystujemy zależność postaci :

δ = P_ykr
- a

Równanie to jest liniowe względem współrzędnych
oraz δ , wyznacz więc prostą o współczynniku kierunkowym tgγ = P_ykr.

Dla pręta jak na rysunku mamy więc wykres zależności :

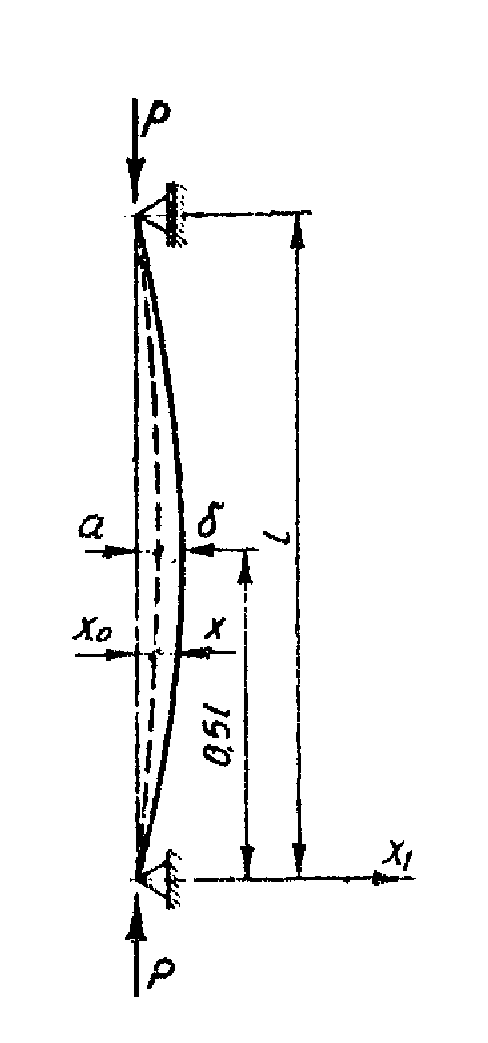
Określenie więc podczas badań, w postaci dyskretnej, zależności δ_i = f (
) , a następnie aproksymacja otrzymanych wyników prostą δ = η
+ ϑ , której parametry η , ϑ obliczamy np. metodą najmniejszych kwadratów, umożliwia wyznaczenie wartości obciążenia krytycznego oraz krzywizny początkowej pręta :

P^d_ykr = η , a = ϑ.

Aby wykreślnie wyznaczyć obciążenie krytyczne metodą Southwella, należy na podstawie wyników pomiarów sporządzić wykres zależności δ = f (
) , który powinien być linią prostą, a następnie na jego podstawie wyznaczyć obciążenie krytyczne :

P^d_ykr = tgγ

Z wykresu można także odczytać wielkość a, charakteryzującą krzywiznę początkową pręta.

Schemat stanowiska badawczego do wyznaczania siły krytycznej wyboczenia giętnego dla pręta o przekroju w kształcie wąskiego prostokąta :

3. Przebieg ćwiczenia

a) inwentaryzacja przekroju :

h

` l b

l = 200 mm

h = 12,1 mm

b = 5,1 mm

b) wyznaczenie momentu bezwładności przekroju oraz wartości siły krytycznej:

I­_y =
=
= 0,01337*10­^-8 m⁴

P_ykr =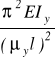
=
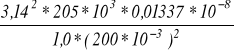
= 6,763*10^-3 MN

0,7*P_ykr = 0,7 * 6,763*10^-3 = 4,734*10^-3 MN

( wartość siły do której obciążamy próbkę przyjmujemy 4,8*10^-3 MN )

c) wyniki pomiarów

Lp.	Obciążenie	Wskazania czujnika		Ugięcie pręta		Ugięcie śr.	δi/Pi
		*10^-3[MN]	wl [mm]	wp [mm]	δi = wi - wo [mm]		[mm]	[mm/MN]
1	0,00	4,51	5,42	0,00	0,00	0	0,000
2	0,80	4,54	5,40	0,03	0,02	0,025	31,250
3	1,60	4,63	5,31	0,12	0,11	0,115	71,875
4	2,40	4,74	5,20	0,23	0,22	0,225	93,750
5	3,20	4,92	5,01	0,41	0,41	0,41	128,125
6	4,00	5,17	4,75	0,66	0,67	0,665	166,250
7	4,80	5,50	4,42	0,99	1,00	0,995	207,292
8	4,00	5,13	4,80	0,62	0,62	0,62	155,000
9	3,20	4,95	4,97	0,44	0,45	0,445	139,063
10	2,40	4,79	5,15	0,28	0,27	0,275	114,583
11	1,60	4,64	5,30	0,13	0,12	0,125	78,125
12	0,80	4,54	5,40	0,03	0,02	0,025	31,250
13	0,00	4,47	5,48	-0,04	-0,06	-0,05	0,000

Do wykresu uśredniono wartości δ_i/P_i dla obciążania i odciążania próbki.

c) Obliczenie procentowej różnicy między wartością siły krytycznej wyznaczonej teoretycznie i doświadczalnie :

Z wykresu możemy odczytać : P^d_ykr = tgγ = 4,9*10^-3 MN

Siła wyznaczona teoretycznie : P_ykr = 6,763*10^-3 MN

Różnica wartości : Δ =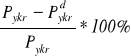
=
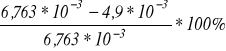
= 27,5%

4. Wnioski

Jak możemy zauważyć różnica wartości teoretycznej i doświadczalnej jest znaczna (sięga 27,5% ). Błędu, który został tutaj popełniony, możemy doszukiwać się w tym, że badany pręt mógł zostać zamocowany przez laboranta niedokładnie w pionie, poza tum czujniki mogły nie być przyłożone w środku rozpiętości pręta, jednak największy błąd spowodowany był wyeksploatowanymi już czujnikami pomiarowymi ( aby można było odczytywać wartości należało delikatnie uderzać w zegary ). Spowodowało to iż po zdjęciu obciążenia według wskazań czujników pręt wygiął się w przeciwnym kierunku co jest rzeczą niemożliwą. Otrzymaną więc wartość obciążenia krytycznego nie można uznać za wiarygodną.

---