Zadanie 1.
Dane:
numer |
X |
Y |
Hnor |
Hgeom |
ζ |
1 |
5785641,62 |
7499463,69 |
111,253 |
144,969 |
33,716 |
2 |
5789412,28 |
7500120,3 |
136,28 |
169,835 |
33,555 |
3 |
5793398,99 |
7499833,11 |
122,586 |
155,995 |
33,409 |
4 |
5796335,04 |
7499860,71 |
156,343 |
189,649 |
33,306 |
5 |
5800229,11 |
7499659,73 |
165,251 |
198,439 |
33,188 |
6 |
5803567,08 |
7500019,86 |
112,586 |
145,673 |
33,087 |
7 |
5785735,43 |
7501742,97 |
116,253 |
149,938 |
33,685 |
8 |
5789691,52 |
7502026,05 |
122,382 |
155,9 |
33,518 |
9 |
5792627,33 |
7501738,09 |
143,128 |
176,538 |
33,41 |
10 |
5796614,28 |
7501897,05 |
135,382 |
168,644 |
33,262 |
11 |
5800230,16 |
7501751,73 |
134,128 |
167,277 |
33,149 |
12 |
5803259,22 |
7502110,7 |
179,282 |
212,338 |
33,056 |
13 |
5785645,09 |
7504232,19 |
158,282 |
191,939 |
33,657 |
14 |
5789415,88 |
7504504,01 |
156,254 |
189,748 |
33,494 |
15 |
5792784,44 |
7504385,48 |
165,493 |
198,856 |
33,363 |
16 |
5797265,71 |
7504341,86 |
134,782 |
167,983 |
33,201 |
17 |
5800541,64 |
7504261,76 |
140,253 |
173,348 |
33,095 |
18 |
5803323,47 |
7504486,45 |
147,675 |
180,683 |
33,008 |
19 |
5785740,78 |
7506330,18 |
136,085 |
169,706 |
33,621 |
Lokalne funkcje opisujące geoidę wg modelu płaszczyzny:
![]()
Postać macierzowa:
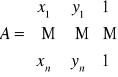
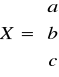
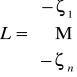
Równanie normalne:
![]()
Rozwiązując otrzymujemy:
![]()
Rozwiązanie:
a= |
-3,58239E-05 |
b= |
-1,45244E-05 |
c= |
33,35684211 |
Obliczamy ![]()
,![]()
oraz ich różnicę:
Numer |
ζ obl |
ζ pom |
δ |
20 |
33,45697652 |
33,448 |
0,008977 |
21 |
33,32948601 |
33,305 |
0,024486 |
22 |
33,20183418 |
33,174 |
0,027834 |
23 |
33,07419138 |
33,055 |
0,019191 |
24 |
32,95385665 |
32,95 |
0,003857 |
25 |
33,57824921 |
33,59 |
-0,011751 |
26 |
33,42110466 |
33,4 |
0,021105 |
27 |
33,29557776 |
33,261 |
0,034578 |
28 |
33,17100095 |
33,132 |
0,039001 |
29 |
33,03895533 |
33,008 |
0,030955 |
30 |
32,92332643 |
32,901 |
0,022326 |
![]()
0.019 m
Lokalne funkcje opisujące geoidę wg modelu wielomianowego drugiego stopnia:
![]()
Postać macierzowa:
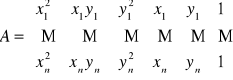
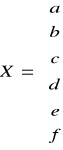
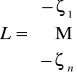
Równanie normalne:
![]()
Rozwiązując otrzymujemy:
![]()
Rozwiązanie:
a= |
-3,61897E-05 |
b= |
-1,70548E-05 |
c= |
-3,57331E-10 |
d= |
4,32069E-10 |
e= |
-2,50254E-10 |
f= |
33,28687049 |
Obliczamy ![]()
,![]()
oraz ich różnicę:
Numer |
ζ obl |
ζ pom |
δ |
20 |
33,448 |
33,44175 |
-0,00625 |
21 |
33,305 |
33,3032 |
-0,0018 |
22 |
33,174 |
33,17482 |
0,000822 |
23 |
33,055 |
33,05862 |
0,003618 |
24 |
32,95 |
32,95592 |
0,005917 |
25 |
33,59 |
33,58296 |
-0,00704 |
26 |
33,4 |
33,39534 |
-0,00466 |
27 |
33,261 |
33,25933 |
-0,00167 |
28 |
33,132 |
33,13463 |
0,002626 |
29 |
33,008 |
33,01423 |
0,006229 |
30 |
32,901 |
32,91342 |
0,012416 |
![]()
0.005m
Profil modelu geoidy niwelacyjnej:
Katedra Geodezji i Astronomii Geodezyjnej Wtorek
Politechnika Warszawska
Ćwiczenie VI
Niwelacja satelitarna
9 VI 2009 r.
Semestr: 4
Rok akademicki: 2008/2009
Grupa: 3a Piotr Mielnicki
Wyszukiwarka
Podobne podstrony:
PM Cwiczenie IV, gik, semestr 4, Wyższa, Wyższa, Cwiczenia
Cwiczenie I, gik, semestr 4, Wyższa, Wyższa, Cwiczenia
Cwiczenie IV, gik, semestr 4, Wyższa, Wyższa, Cwiczenia
PM Cwiczenie I, gik, semestr 4, Wyższa, Wyższa, Cwiczenia
Cwiczenie V, gik, semestr 4, Wyższa, Wyższa, Cwiczenia
PM Cwiczenie V, gik, semestr 4, Wyższa, Wyższa, Cwiczenia
Cwiczenie Niwelacja Satelitarna-2, gik, semestr 4, Wyższa, Geodezja Wyższa, odstep geoidy cw7
Pytania z 2 kolokwium, gik, semestr 4, Wyższa, Wyższa, kolo-2-z-cwiczen
Cw1-dziennik niwelacyjny, gik, semestr 4, Wyższa, Wyższa, Cwiczenia
stabilizacja, gik, semestr 4, Wyższa, Geodezja Wyższa, osnowa wysokosciowa
analiza techniczna, gik, semestr 4, Wyższa, Geodezja Wyższa, osnowa wysokosciowa
Sciaga gedezja sprawdzian nr.2, gik, semestr 4, Wyższa, GW
Sciaga Kolos I, gik, semestr 4, Wyższa, kolo1
ćw, gik, semestr 4, Wyższa, Geodezja Wyższa, odstep geoidy cw7
wsp ptk, gik, semestr 4, Wyższa, Geodezja Wyższa, ćw1 precyzyjna
charakterystyka, gik, semestr 4, Wyższa, Geodezja Wyższa, osnowa wysokosciowa
więcej podobnych podstron