Wstęp teoretyczny

Kodowanie jest umową, określającą wektor informacji cyfrowej odpowiadający każdemu elementowi danego zbioru symboli. Kodem danego zbioru symboli ( cyfr, liter znaków pisarskich, logicznych, arytmetycznych ) nazywa się przyporządkowanie każdemu symbolowi tego zbioru jednego i tylko jednego wektora informacji cyfrowej. Z tej definicji wynika informacja, że kod nie musi być przyporządkowaniem wzajemnie jednoznacznym. W celu uniknięcia błędów koduje się za pomocą wektorów bajtowych, których ósmy bit jest bitem kontrolnym ( bitem kontroli parzystości ) umożliwiającym wykrycie przekłamania na pozycji pojedynczego bitu w bajcie. Przed wprowadzeniem bajtu z klawiatury, bit kontroli parzystości zostaje ustawiony tak, aby całkowita liczba jedynek w bajcie była parzysta lub równa zeru, np.:

1. 101101 dołączmy bit kontroli parzystości równy 1.

2. 1000111 dołączmy bit kontroli parzystości równy 0.

Kontrolę parzystości można wykonać także odwrotnie, tzn. bit kontroli parzystości ustawiamy tak, aby całkowita liczba jedynek była nieparzysta.

Kody liczbowe

W mikrosystemach stosowane są różnorodne sposoby kodowania liczb, zależne jest to od

• natury liczb

• pochodzenia liczb

• przeznaczenia liczb

Kod binarny prosty ( dwójkowy) - stosowany do kodowania liczb całkowitych dodatnich Kod binarny prosty przyporządkowuje liczbom dziesiętnym całkowitym dodatnim X­­₍₁₀₎ o wartościach z przedziału 0 ≤ X₍₁₀₎ ≤ 2ⁿ -1 n - bitowe wektory informacji cyfrowej zwane również liczbami binarnymi n - bitowymi

a_n-1 , a_n-2 , ... , a₀ , a_i ∈ {0,1}

przy czym

X₍₁₀₎ = 2^n-1*a_n-1 + 2^n-2*a_n-2+...+a₀

Kod binarny prosty dla n = 3

0 ≤ X(10) ≤ 7	a2	a1	a0
0 1 2 3 4 5 6 7	0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1

Kod dwójkowy - dziesiętny ( kod BCD - ang. Binary Code Decimal ) przyporządkowuje liczbom dziesiętnym od 0 do 9 4-bitowe wektory informacji cyfrowej zwane z tego powodu kęsami BCD. Zastosowanie kodów BCD dla liczb dziesiętnych polega na zastępowaniu każdej cyfry dziesiętnej odpowiadającymi jej kęsami BCD, np. w kodzie 8481:

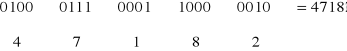
Najczęściej stosowane kody dwójkowo - dziesiętne

X(10)	Kod 8421	Kod Excess-3	Kod 2421
0 1 2 3 4 5 6 7 8 9	0000 0001 0010 0011 0100 0101 0110 0111 1000 1001	0011 0100 0101 0110 0111 1000 1001 1010 1011 1100	0000 0001 0010 0011 0100 1011 1100 1101 1110 1111

Kod dopełnieniowy do dwóch przyporządkowuje liczbom dziesiętnym całkowitym X₍₁₀₎ o wartościach z przedziału -2^n-1 ≤ X₍₁₀₎ ≤ 2^n-1-1 n - bitowe wektory informacji cyfrowej

a_n-1 , a_n-2 , ... , a₀ , a_i ∈ {0,1}

przy czym

X₍₁₀₎ = -2^n-1*a_n-1 + 2^n-2*a_n-2+...+a₀

przyporządkowuje liczbom dziesiętnym ułamkowym X₍₁₀₎ o wartościach z przedziału

-1 ≤ X₍₁₀₎ ≤ 1 -

n - bitowe wektory informacji cyfrowej

a_n-1 , a_n-2 , ... , a₀ , a_i ∈ {0,1}

przy czym

X₍₁₀₎ = - a_n-1 +
a_n-2 +
a_n-3 + ... +
a₀

Dopełnienie do dwóch dowolnej liczby binarnej można uzyskać zmieniając wszystkie bity na przeciwne i dodając 1 do bitu najmniej znaczącego np.:

X(10) całkowita	X(10) ułamkowa	a3	a2	a1	a0
0 1 2 3 4 5 6 7 -8 -7 -6 -5 -4 -3 -2 -1	0 0,125 0,250 0,375 0,500 0,625 0,750 0,875 -1,000 -0,875 -0,750 -0,625 -0,500 -0,375 -0,250 -0,125	0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1	0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1

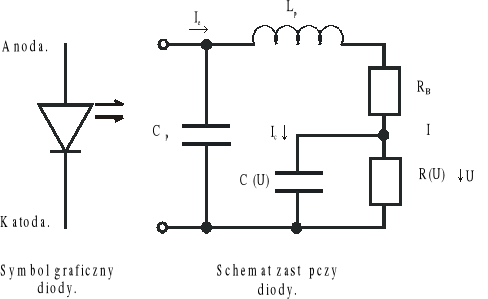
Zasada działania Diod „LED”

Diody „LED” są półprzewodnikowymi źródłami promieniowania opartymi na wykorzystaniu zjawiska promienistej rekombinacji nośników ładunków wstrzykiwanych przez złącze p-n. Podstawą działania „LED” jest zjawisko elektroluminescencji polegającej na zamianie, w wyniku rekombinacji promienistej energii nośników ładunku na energię promienistą. W wyniku rekombinacji nośniki ładunku przechodzą ze stanów o wyższej energii do stanów o energetycznie niżej położonych oddając swoją energię innym nośnikom ładunków, albo atomom sieci krystalicznej, albo też oddając ją w postaci fotonów.

---