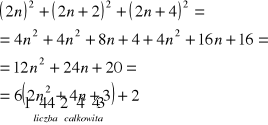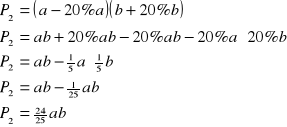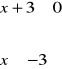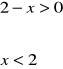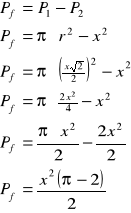KLUCZ - grupa A
III Wojewódzki Konkurs Matematyczny dla uczniów gimnazjum
eliminacje szkolne 2002/2003
Uczeń ma wybrać i rozwiązać pięć spośród sześciu zadań.
Uczeń może maksymalnie uzyskać 30 punktów.
Wszystkie zadania są tak samo punktowane ( po 6 punktów ).
Do etapu rejonowego kwalifikuje zdobycie co najmniej 27 punktów, co stanowi 90% punktów możliwych do uzyskania za poprawne rozwiązanie pięciu zadań.
Nr zad. |
Rozwiązanie |
Punktacja |
1. |
Trzy kolejne liczby parzyste:
Iloczyn liczby 6 przez dowolną liczbę całkowitą jest podzielny przez 6, więc liczba postaci
|
1p.
1p.
2p.
2p.
łącznie 6p. |
2. |
Boki I prostokąta: Boki II prostokąta: a a - 20% a b b + 20% b Pole I prostokąta:
|
1p. za oznaczenie boków i zapisanie pola pierwszego prostokąta.
1p.
2p.
1p.
1p.
łącznie 6p. |
Nr zad. |
Rozwiązanie |
Punktacja |
3. |
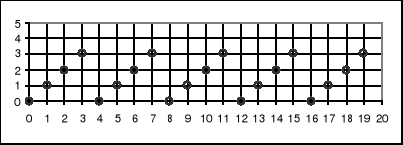
Df : x ∈ { 0, 1, 2, 3, ..., 19 }
x 0 1 2 3 4 5 6 7 8 9
y 0 1 2 3 0 1 2 3 0 1
x 10 11 12 13 14 15 16 17 18 19
y 2 3 0 1 2 3 0 1 2 3
|
1p. 1p. 1p.
1p. za tabelkę wartości.
2p. (punkty na wykresie nie mogą być połączone).
łącznie 6. |
4. |
-3 2 x
|
2p. za zapisanie nierówności. 2p. za rozwiązanie nierówności.
1p.
1p.
łącznie 6p. |
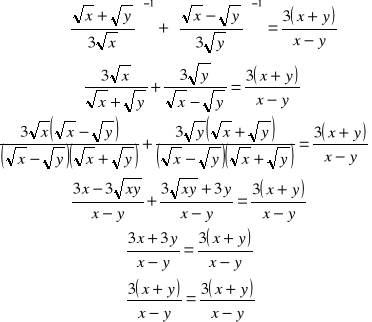
5. |
|
1p.
2p.
1p.
1p.
1p.
łącznie 6p. |
Nr zad. |
Rozwiązanie |
Punktacja |
6. |
P1 - pole koła P2 - pole kwadratu Pf = ?
|
1p. za rysunek z oznaczeniami.
1p. za obliczenie promienia.
1p.
1p.
1p.
1p.
łącznie 6p. |
1
Hanna Kozłowska, Katarzyna Matuszek, Antonina Wiącek
Gimnazjum nr 27 z Oddziałami Integracyjnymi w Poznaniu
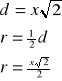
°
y
x
d
•
r
x
x
Wyszukiwarka
Podobne podstrony:
2002 2003 szkolny test
Ginekologia 2002 2003, gielda(1)
klucz odpowiedzi 2003
psychologia spoeczna-wykad , PSYCHOLOGIA SPO?ECZNA - WYK?ADY 2002/2003
ISUZU AXIOM 2002 2003
2002 2003 wojewódzki test
brzuch i miednica 2002 2003 17 01
brzuch i miednica 2002 2003 16 01
egzamin 2002-2003, Notatki, Elektronika AGH III rok, [STUDIA] rok 3, Sieci, Egzamin - sieci, Egzam
Anatomia gieldaEgzamin II 2002-2003, anatomia
Prawo cywilne 3-3, ZAGADNIENIA OBJĘTE ZAKRESEM EGZAMINU - ROK AKADEMICKI 2002/2003
LAND ROVER FREELANDER 2002 2003
Międzyszkolne Zawody Matematyczne 2002-2003, Klasa IV(1)
Alicja Siemak-Tylikowska - Dydaktyka ogólna (wyklady 2002-2003), Pedagogika UW
Karta odpowiedzi - Międzyszkolne Zawody 2002-2003, Klasa IV(1)
Prawo cywilne 1-1, ZAGADNIENIA OBJĘTE ZAKRESEM EGZAMINU - ROK AKADEMICKI 2002/2003
Sieci -Jelenia Gra - 2002-2003- rozw , Elektronika i Telekomunikacja PWR, 3 rok
mat 2002 2003 iii
więcej podobnych podstron