• ŻEBRO

1. Rozpiętość przęseł:

l₀₁ = l₀₂ = 6,4 x 1,025 =6,56 m

osiowy rozstaw żeber a = 2,00 m

2. Przekrój żebra:

b = 0,20 m; h = 0,45 m

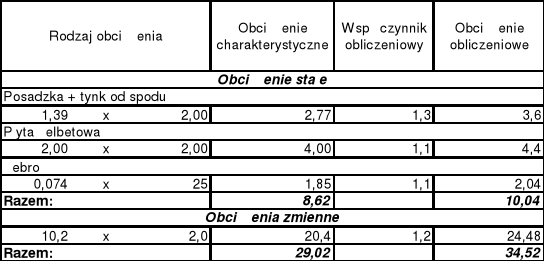
3. Zebranie obciążeń:




4. Obliczenie momentów oraz sił przekrojowych według współczynników WINKLERA

M1-2 =	(0,070 x 10,04 + 0,096 x 24,48) x 6,56^2	= 131,38 kNm
M2-3 min =	(0,070 x 10,04 - 0,025 x 24,48) x 6,56^2	= 3,91 kNm
M2 =	-0,125 x 34,52 x 6,56^2	= -185,69 kNm
M2 min =	(-0,125 x 10,04 + 0,063 x 24,48) x 6,56^2	= 12,36 kNm
V1 =	(0,375 x 10,04 + 0,437 x 24,48) x 6,56	= 94,88 kN
V2^L=V2^P =	0,625 x 34,52 x 6,56	= 141,53 kN

5. Wymiarowanie przekroju

b_w = 0,20 m; l_eff = 6,56 m; M_sd= 131,38 kNm

h = 0,45 m; a₁= 0,04 m; h_f = 0,08 m

d = 0,45 - a₁ = 0,45 - 0,04 = 0,41 m

Beton B-25 fcd = 13,3 Mpa

Stal A - III fyd = 350 MPa

1. Przęsło 1 - 2

b_eff = b_w +
lo = 0,7 x l_eff = 0,7 x 6,56 = 4,59 m

b_eff = 0,20 +
= 1,12 m

b_eff1 = b_eff2 =6 x h_eff =6 x 0,08 = 0,48 m

b_eff = 2 x 0,48 + 0,20 =1,16 m

Przyjęto: b_eff = 1,12 m

1. Sprawdzenie położenia osi obojętnej x_eff = h_f

Msd (h_f) = α x fcd x b_eff x h_f x(d-0,5 h_f)

Msd (h_f) = 0,85 x 13,3 x 1,12 x 0,08 x (0,41 - 0,5 x 0,08) = 0,375 kNm

Msd (h_f) =375,0 > Msd = 131,38 kNm

Oś obojętna znajduje się w płycie, przekrój pozornie teowy x_eff < h_f

Przekrój liczymy jako prostokąt o wymiarach b_eff x h_f

Ao =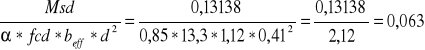


ξ _eff=1 -
=1 -
=0,032

ϕ = 1 - 0,5ξ _eff =1 - 0,5 x 0,032 = 0,984

A_s1 =
m² = 9,30 cm²

Przyjęto: zbrojenie dołem 3 φ 20 o A_s1 = 9,42 cm²

zbrojenie górą 2 φ 12

2. Podpora 2

Msd ₍₂₎= Msd + V
= -185,99+141,53 x
-171,84 kNm

Msd ₍₂₎= -0,17184 MNm

W środku podpory:

Ao =


ξ _eff=1 -
=1 -
=0,26

ϕ = 1 - 0,5ξ _eff =1 - 0,5 x 0,26 = 0,87

A_s1 =
m² = 13,8 cm²

Przyjęto: zbrojenie górą na podporze 3 φ 25 o A_s1 = 14,72 cm²

3. Przęsło 2 - 3

b_eff = b_w +
lo = 0,7 x l_eff = 0,7 x 6,56 = 4,59 m

b_eff = 0,20 +
= 1,12 m

b_eff1 = b_eff2 =6 x h_eff =6 x 0,08 = 0,48 m

b_eff = 2 x 0,48 + 0,20 =1,16 m

Przyjęto: b_eff = 1,12 m

1. Sprawdzenie położenia osi obojętnej x_eff = h_f

Msd (h_f) = α x fcd x b_eff x h_f x(d-0,5 h_f)

Msd (h_f) = 0,85 x 13,3 x 1,12 x 0,08 x (0,41 - 0,5 x 0,08) = 0,375 kNm

Msd (h_f) =375,0 > Msd = 131,38 kNm

Oś obojętna znajduje się w płycie, przekrój pozornie teowy x_eff < h_f

Przekrój liczymy jako prostokąt o wymiarach b_eff x h_f

Ao =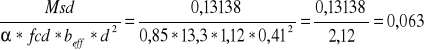


ξ _eff=1 -
=1 -
=0,032

ϕ = 1 - 0,5ξ _eff =1 - 0,5 x 0,032 = 0,984

A_s1 =
m² = 9,30 cm²

Przyjęto: zbrojenie dołem 3 φ 20 o A_s1 = 9,42 cm²

zbrojenie górą 2 φ 12

6. Obliczanie przekroju na ścinanie

1. Podpora 1

Vsd _max = 94,88 kN; a = 0,15 m

(g+p) = 34,52 kNm²

1. Siła poprzeczna na krawędzi podpory

Vsd* = Vsd_max - a x (g+p) = 94,88 - 0,15 x 34,52 =89,70 kN

2. Siła poprzeczna na odległości „d” od krawędzi podpory

Vsd = Vsd_max - (a +d) x (g+p) = 94,88 - (0,15+0,41) x 34,52 =75,55 kN

3. Sprawdzenie czy obliczenie ścinania jest konieczne

Obliczenie siły granicznej V_RD1

V_RD1 = [1,4 x k x τ_RD x (1,2 + 40ρ_L)+0,5σ_cp] x b_w x d

k = 1,6 - d = 1,6 - 0,41 = 1,19

τ_RD = 0,26 z tab. 13 normy

ρ_L =


σ_cp = 0

V_RD1 = [1,4 x 1,19 x 0,26 x (1,2+40 x 0,0114)] x 0,2 x 0,41= 0,059 MN

V_RD1 =59,0 kN < Vsd = 75,55 kN

Obliczenie odcinka drugiego rodzaju

l_t =
m

Sprawdzenie warunku Vsd ≤ V_RD2

Zakładam zbrojenie poprzeczne tylko z strzemion, wtedy wzór na V _RD2 ma postać:

V _RD2 =


ν = 0,7 -


z = 0,9 x d =0,9 x 0,41 =0,369

przyjmuję ctgθ =ctg45^o = 1

V _RD2 =
0,294 MN= 294,0 kN

V _RD2 = 294,0 > Vsd =75,55 kN

Uwaga: Warunek został spełniony

Maksymalny rozstaw strzemion obliczony z warunku:

Vsd ≤


Smax = 0,8 d ≤ 300 mm

Smax = 0,8 x 0,41 = 0,328 mm

Przyjęto Smax = 0,30 m

Zakładam strzemiona φ 8 dwuramienne

V_RD3 =



m

Przyjmuję strzemiona co 18 cm na odcinku drugiego rodzaju równym l_t= 0,89 m na dalszym odcinku co 30 cm.

2. Podpora 2 (z lewej)

Vsd _max = 141,53 kN; a = 0,15 m

(g+p) = 34,52 kNm²

1. Siła poprzeczna na krawędzi podpory

Vsd* = Vsd_max - a x (g+p) = 141,53 - 0,15 x 34,52 =136,35 kN

2. Siła poprzeczna na odległości „d” od krawędzi podpory

Vsd = Vsd_max - (a +d) x (g+p) = 141,53 - (0,15+0,41) x 34,52 =122,19 kN

3. Sprawdzenie czy obliczenie ścinania jest konieczne

Obliczenie siły granicznej V_RD1

V_RD1 = [1,4 x k x τ_RD x (1,2 + 40ρ_L)+0,5σ_cp] x b_w x d

k = 1,6 - d = 1,6 - 0,41 = 1,19

τ_RD = 0,26 z tab. 13 normy

ρ_L =


σ_cp = 0

V_RD1 = [1,4 x 1,19 x 0,26 x (1,2+40 x 0,0179)] x 0,2 x 0,41= 0,068 MN

V_RD1 =68,0 kN < Vsd = 136,35 kN

Obliczenie odcinka drugiego rodzaju

l_t =
m

Sprawdzenie warunku Vsd ≤ V_RD2

Zakładam zbrojenie poprzeczne tylko z strzemion, wtedy wzór na V _RD2 ma postać:

V _RD2 =


ν = 0,7 -


z = 0,9 x d =0,9 x 0,41 =0,369

przyjmuję ctgθ =ctg45^o = 1

V _RD2 =
0,294 MN= 294,0 kN

V _RD2 = 294,0 > Vsd =136,35 kN

Uwaga: Warunek został spełniony

Maksymalny rozstaw strzemion obliczony z warunku:


<Vsd ≤


Smax = 0,6 d ≤ 300 mm

Smax = 0,6 x 0,41 = 0,246 mm

Przyjęto Smax = 0,25 m

Zakładam strzemiona φ 8 dwuramienne

V_RD3 =



m

Przyjmuję strzemiona co 15 cm na odcinku drugiego rodzaju równym l_t= 1,98 m na dalszym odcinku co 25 cm.

3. Podpora 2 (z prawej)

Z uwagi na tę samą siłę tnącą co po lewej stronie, zbrojenie przyjmuje się jak dla lewej strony.

4. Podpora 3

Z uwagi na tę samą siłę tnącą i rozpiętości zbrojenie przyjmuje się jak dla podpory pierwszej.

7. Obliczenie ugięcia żebra

Msd = 131,38

Msd^d =
kNm

Dane:

b_w = 0,20 m; h = 0,45 m; d = 0,41m; l_eff = 5,84m

A - III 3 φ 20 o As = 9,42 cm² ; ρ_L =


fyd = 350 Mpa; E_s = 200000 MPa

B- 25 fctm = 2,20 MPa, Ecm = 29000 MPa, fcd = 13,3 MPa, t_o = 90 dni, t = 730 dni

Mcr = fctm x Wc

Wc =
m³

Mcr =2000 x 0,007 = 14,0 kNm < Msd = 131,38 kNm

Obliczenie ugięcia ze wzoru

a =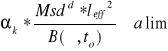


α_k =


B(∞)=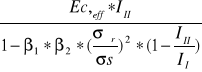


β₁ = 1,0 - dla prętów żebrowanych

β₂ = 0,5 - dla obciążeń długotrwałych




Ec,_eff =
φ z tablicy 3 (h_o
;t_o)

h_o =
;  = 2,27

Ec,_eff =
MPa

α_e,t =


Obliczenie momentu bezwładności w fazie pierwszej dla przekroju niezarysowanego Ia

I_I

X_I=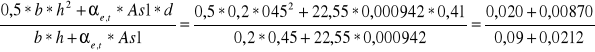
=

X_I =
cm

I_I =
=

I_I =


I_I =
m⁴

Obliczenie fazy zarysowanej

X_II =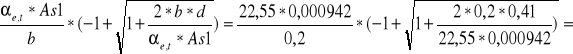


X_II =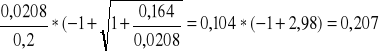
m

I_II =
=

I_II = 0,0006+0,00083 = 0,00146 = 1,46 x 10^-3 m⁴

B(∞)=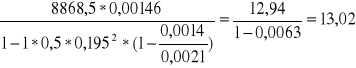
MN/m²

a =


Uwaga: Warunek został spełniony

Sprawdzenie szerokości rozwarcia rys prostopadłych do osi belki

Mcr = 14,0 kNm < Msd^d =72,99 kNm

w = β x S_rm x ε_sm <w_lim

β = 1,7 - współczynnik wyrażający obliczeniowe szerokości rysy do szerokości środnika

S_rm = 50 + 0,25 x k₁ x k₂ x


k₁ = 0,8 - współczynnik dla prętów żebrowanych

k₂ = 0,5 - dla zginania

φ = 20 mm - średni przekrój zbrojenia




Act,_eff - efektywna powierzchnia rozciąganej strefy betonu

Act,_eff =2,5(0,45-0,41) x 0,20 = 0,03 m²




S_rm = 50 + 0,25 x 0,8 x 0,5 x
= 95,4 mm

ε_sm - średnie odkształcenie zbrojenia rozciąganego, szerokość rysy jest równa wydłużeniu zbrojenia

ε_sm =



MPa

β₁ = 1,0 - dla prętów żebrowanych

β₂ = 0,5 - dla obciążeń długotrwałych




ε_sm =


w = β x S_rm x ε_sm <w_lim = 0,3 mm

w = 1,7 x 95,4 x 0,00209 = 0,29 mm < w_lim = 0,3 mm

Projekt stropu żebrowego - żebro 13

POLITECHNIKA POZNAŃSKA

INSTYTUT KONSTRUKCJI BUDOWLANYCH

Zakład Konstrukcji Żelbetowych




---