1. Uzasadnij dzięki czemu jesteśmy zdolni naukowo przewidywać przyszłość?

2. Scharakteryzuj najważniejsze funkcje prognoz.

3. Scharakteryzuj etapy procesu prognozowania.

4. Klasyfikacja prognoz.

5. Podstawowe założenia klasycznej teorii predykcji:

6. Czynniki wpływające na trafność prognozy oraz przesłanki decydujące o wyborze metody prognozowania:

7. Podstawowe zasady predykcji: (zasady budowy prognoz):

8. Prognoza przedziałowa i punktowa.

9. Jaka prognozę możemy uznać za dopuszczalną?

10. Krótko scharakteryzuj podstawowe elementy szeregów czasowych:

11. Podstawowe mierniki ex-post.

12. W jakich sytuacjach można stosować do prognozowania modele średniej ruchomej?

13. Jak budujemy prognozy na podstawie stacjonarnych szeregów czasowych:

14. Scharakteryzuj metodę heurystyczną:

15. Podaj narzędzia weryfikacji modelu prognostycznego

16. Wymień etapy budowy prognoz dla szeregów czasowych zawierających T, C, S, I.

17. W jaki sposób eliminujemy z szeregu wahania sezonowe?

18. Podaj technikę wyodrębniania i eliminacji z szeregu czasowego tendencji rozwojowej.

19. Co wiesz o dekompozycji szeregu czasowego?

20. Wymień znane ci adaptacyjne metody prognozowania:

21. Co wiesz o prognozowaniu metodą wyrównywania wykładniczego Holta:

22. Jakie znasz heurystyczne metody prognozowania i wymień etapy postępowania w metodzie delfickiej.

23. Wymień analogowe metody prognozowania i omów wariant wzorca.

24. Wymień znane Ci funkcje prognoz i omów jedną z nich

25. Co wiesz o prognozowaniu metodą Wintersa?

26. Co wiesz o metodach prognozowania koniunktury gospodarczej?

27. Prognozy ostrzegawcze - pojęcie i sposoby.

28. W jakich sytuacjach możemy stosować do prognozowania modele średniej ruchomej?

29. Prognozowanie na podstawie ekstrapolacji funkcji trendu.

30. Podaj sposób wyodrębniania z szeregu czasowego wahań cyklicznych i sezonowych.

31. Zadanie: znając kwartalne addytywne efekty sezonowe sprzedaży konserw: I=0,825, II=2,525, IV= -4,675 ; wyznacz i zinterpretuj efekt sezonowy w III kwartale.

32. Jak graficznie zidentyfikować T C S / Na podstawie wzrokowej oceny szeregów czasowych dokonaj wstępnej identyfikacji elementów szeregu czasowego

1. Uzasadnij dzięki czemu jesteśmy zdolni naukowo przewidywać przyszłość?

Przewidywanie przyszłości to wnioskowanie o zdarzeniach, które zajdą w czasie późniejszym niż czynność przewidywania.

Możemy przewidywać przyszłość, ponieważ w świecie, w którym żyjemy, panuje pewien porządek. Polega on na tym, że zdarzenia powiązane są różnymi zależnościami oraz na tym, że zależności te podlegają pewnym prawidłowościom. Zarówno prawidłowości te, jak i zależności mogą być różnego typu, mogą mieć charakter funkcyjny, przyczynowo - skutkowy, bezpośredni, pośredni, pierwotny, wtórny, główny, uboczny... Znajomość tych związków pozwala wyjaśnić różne prawidłowości występujące w otaczającym nas świecie oraz stanowi podstawę do budowy prognoz.

Stopień przewidywalności jest bardzo zróżnicowany. W naukach technicznych, przyrodniczych można przewidywać z dużą dokładnością. Natomiast w naukach społecznych i ekonomicznych takie ścisłe przewidywanie nie jest możliwe, ponieważ wpływa na to zbyt wiele czynników o charakterze przypadkowym. Nie można przewidywać zjawisk i procesów przypadkowych, losowych i szczególnych. Gdyby w świecie, w którym żyjemy, panował chaos, gdyby wszelkie zdarzenia zachodziły niezależnie jedne od drugich, przewidywanie przyszłości byłoby niemożliwe.

2. Scharakteryzuj najważniejsze funkcje prognoz.

Funkcja strategiczna

polega na tym, ze prognozy mogą stanowić podstawę długofalowego działania lub długofalowej polityki gospodarczej. Informacje z prognoz długookresowych mogą być podstawa wyboru strategii działania dla długiego i krótkiego okresu. Dotyczyć to może takiej decyzji, jak reorganizacja gospodarstwa.

Funkcja ostrzegawcza prognoz

celem tej funkcji jest możliwość podjęcia działań zapobiegawczo - preferencyjnych w odpowiednim czasie. Może to stanowić podstawę różnorodnych działań, np. zmiany strategii działania. Wtedy funkcja ostrzegawcza jest zarazem funkcją strategiczną.

Funkcja weryfikacyjna

występuje wówczas, gdy prognozy dają także wcześniejsze rozeznanie o stopniu realizacji celów. Np. prognozy plonów zbóż wykonane metodami biometrycznymi informują o prawdopodobnych plonach, gdy rośliny są jeszcze na polu. W wyniku takich prognoz mamy rozeznanie co do stopnia realizacji wcześniej założonych zadań.

Funkcja aktywizująca

polega na pobudzeniu do podejmowania działań sprzyjających realizacji prognozy, gdy zapowiada ona zdarzenia korzystne i przeciwstawiających się jej realizacji, gdy przewidywane zdarzenia są oceniane jako niekorzystne.

Ogólnie możemy powiedzieć, ze zadaniem prognoz jest stworzenie dodatkowych przesłanek w procesie podejmowania decyzji i zmniejszanie niepewności.

3. Scharakteryzuj etapy procesu prognozowania.

1. OKREŚLENIE ZAKRESU PROGNOZOWANIA:

Określenie obiektu, zjawiska, zmiennych mających podlegać prognozowaniu, celu wyznaczania prognozy.

2. HORYZONT PROGNOZY:

Określamy jak daleko chcemy prognozować, przewidywać. Im krótszy horyzont tym prognoza jest bardziej szczegółowa.

3. WYBÓR METODY PROGNOZOWANIA:

Zastosowanie metody powinno być poprzedzone szeroką i wnikliwą analizą - aby poznać wady i zalety metod oraz warunki ich stosowania. O wyborze metody decyduje:

• charakter procesu zmian prognozowanego zjawiska

• horyzont czasu objęty prognozą

• rodzaj posiadanych informacji

• możliwości techniczne i osobowe

• ZBIÓR INFORMACJI:

Informacje do budowy prognoz mogą pochodzić z różnych źródeł:

• wewnętrzne: zapisy, rejestry, raporty od jednostki gospodarczej

• zewnętrzne: ustawy, dokumenty rządowe, banki, instytucje naukowe, GUS

Dane są prawdziwe, gdy odpowiadają przedmiotowi, którego dotyczą, gdy są kompletne i wiarygodne.

5. WYKONANIE OBLICZEŃ:

6. WERYFIKACJA - OCENA REALNOŚCI I TRAFNOŚCI:

Jest możliwa dopiero po upływie czasu który obejmuje prognoza.

7. MONITORING:

W celu dokonywania odpowiednich korekt.

4. Klasyfikacja prognoz.

Kryterium podziału	Rodzaje prognoz
Horyzont czasowy	Długo-, średnio- i krótkoterminowe, perspektywiczne i ponadperspektywiczne , operacyjne i strategiczne
Charakter lub struktura	Proste i złożone, ilościowe i jakościowe
Stopień szczegółowości	Ogólne i szczegółowe
Zakres ujęcia	Światowe, międzynarodowe, krajowe i regionalne
Metoda opracowania	Indukcyjne, dedukcyjne, minimalne, średnie, maksymalne, czyste (pierwotne), weryfikowane, modelowe
Cel lub funkcja	Ostrzegawcze, badawcze, normatywne, aktywne, pasywne i inne

5. Podstawowe założenia klasycznej teorii predykcji:

Predykcja: proces ekonometrycznego wnioskowania w przyszłość.

Założenia:

1. Znany jest model ekonometryczny, który wyjaśnia zmiany zmiennej prognozowanej.

2. Zjawiska i procesy opisywane przez model mają strukturę stabilną w czasie czyli model opisujący dane zjawisko będzie aktualny także w przyszłości, nie ulegnie dezaktualizacji.

3. Znane są wartości zmiennych objaśniających dla okresu prognozowanego.

4. Rozkład składnika losowego nie ulega zmianie w czasie czyli jest stacjonarny.

5. Dopuszczalna jest ekstrapolacja modelu poza próbę statystyczną.

6. Czynniki wpływające na trafność prognozy oraz przesłanki decydujące o wyborze metody prognozowania:

Trafność prognozy: to prawdopodobieństwo spełnienia się przewidywania.

Czynniki:

• HORYZONT PROGNOZY: jest to okres na jak długo przewidujemy przyszłość. Im horyzont prognozy jest dalszy, tym prawdopodobieństwo zaistnienia przewidywanego stanu maleje. Prognozy o długim horyzoncie nie są przydatne dla praktyki gospodarczej i należy z nich rezygnować.

• GŁĘBOKOŚĆ RETROSPEKCJI: jest to długość okresu, w którym obserwuje się zjawisko stanowiące przedmiot prognozy. W długim okresie można wykryć więcej czynników określających dane zjawisko, siłę ich wpływu i znaczenie. Im dłużej obserwujemy tym łatwiej jest określić czynniki istotne a pominąć przypadkowe.

• METODY PROGNOSTYCZNE: do budowy prognoz należy stosować takie metody, które najlepiej odzwierciedlają rzeczywistość gospodarczą w zakresie danego zjawiska. O wyborze metody prognozowania decyduje:

• specyfika rozpatrywanej sytuacji

• charakter zmian

• właściwości metod

• horyzont prognozy

• rodzaj informacji którą dysponujemy

• możliwości techniczne i osobowe

• koszty zastosowania metody

• INFORMACJE PROGNOSTYCZNE: są to dane statystyczne, jakie posiadamy, ważne jest aby poprawnie określały dane zjawisko. Prognoza zbudowana na podstawie błędnych i niekompletnych informacji, niezgodnych z rzeczywistym poziomem zjawisk w przeszłości nie odzwierciedli także prawidłowo przebiegu zjawisk w przyszłości.

7. Podstawowe zasady predykcji: (zasady budowy prognoz):

1. ZASADA PREDYKCJI NIEOBCIĄŻONEJ: Stosuje się ją wtedy, gdy wnioskowanie jest wielokrotnie powtarzane. Nieobciążoność predykcji oznacza, że w przypadku wielokrotnego powtarzania procesu wnioskowania błędy prognoz będą miały charakter losowy o średniej 0 i nie będą występować błędy systematyczne.

2. ZASADA PREDYKCJI NAJWIĘKSZEGO PRAWDOPODOBIEŃSTWA: kiedy prognozujemy kilka razy lub tylko jeden raz wtedy ważne jest aby prognoza miała duże szanse okazać się trafną.

3. ZASADA PREDYKCJI MINIMALIZUJĄCEJ OCZEKIWANĄ STRATĘ: stosujemy ją gdy w ślad za zbudowaniem prognozy idzie odpowiednia działalność gospodarcza, a więc błędna prognoza prowadzi do strat.

4. ZASADA PREDYKCJI PUNKTOWEJ I PRZEDZIAŁOWEJ:

• punktowa: polega na wyborze jednej liczby, uznanej za najlepszą w danych warunkach

• przedziałowa: polega na wyznaczeniu przedziału liczbowego któremu można przypisać prawdopodobieństwo że wartość zmiennej prognozowanej się w nim znajdzie ( przedział predykcji ).

8. Prognoza przedziałowa i punktowa.

Predykcja punktowa polega na wyborze jednej liczby, uznanej za najlepszą, w danych warunkach, ocenę wartości interesującej nas zmiennej w przyszłym okresie.

Predykcja przedziałowa - polega na wyznaczeniu przedziału liczbowego (Ip) o takiej właściwości, ze można mu przypisać rozsądnie bliskie jedności prawdopodobieństwo tego, ze rzeczywista wartość zmiennej prognozowanej znajdzie się w tym przedziale. Przedział ten nazywa się przedziałem predykcji i można go zapisać następująco:

P{Yt+p E Ip}= gama

Gdzie: P - prawdopodobieństwo

Gama - z góry obrana wartość; najczęściej przyjmuje się za gamę liczby: 0,9 i 0,95.

Chcąc zbudować przedział, konieczna jest znajomość rozkładu zmiennej prognozowanej.

9. Jaka prognozę możemy uznać za dopuszczalną?

Prognoza dopuszczalna (dla określonej zmiennej i ustalonego okresu) jest to najczęściej ta prognoza, która została zbudowana zgodnie z teorią predykcji i rząd jej dokładności jest dostateczny w świetle wybranych mierników tej dokładności. Najczęściej przyjmuje się błąd średni predykcji (SBP). Za prognozę dopuszczalną uznaje się te, której lad średni predykcji jest niższy od przyjętej liczby „fi”. Wartość „fi” wynika z konkretnych warunków praktycznych wymaganej dokładności przewidywania. Może on kształtować się różnie dla zmiennych prognozowanych. Praktycznie w rolnictwie za prognozę dopuszczalną uważa się tą, której błąd średni prognozy nie jest większy niż 5% wartości oszacowanych prognoz.

10. Krótko scharakteryzuj podstawowe elementy szeregów czasowych:

Szereg czasowy - poziom zjawiska przedstawiony w czasie.

W każdym szeregu czasowym występuje zawsze co najmniej jeden z następujących elementów:

1. WAHANIA PRZYPADKOWE (I): zwane nieregularnymi, losowymi bądź incydentalnymi. Wynikają z czynników nie dających się przewidzieć. Mogą wynikać z wpływu czynników biologiczno - klimatycznych na wyniki produkcyjne i ekonomiczne rolnictwa, nagłych zmian polityki rządu i innych nie przewidzianych czynników.

2. WAHANIA SEZONOWE (S): to takie zmiany, które powtarzają się regularnie w tym samym okresie każdego roku, wahania te występują wokół stałego (przeciętnego) poziomu lub wokół trendu zmiennej i wyrażają wpływ zachowań ludzi wynikających z kalendarza czy specyfiki produkcji, na kształtowanie się zmiennej prognozowanej. (np. większa podaż zbóż po żniwach, większa produkcja mleka w okresie wiosny i lata).

3. WAHANIA CYKLICZNE (C): wyrażają się w postaci długookresowych, rytmicznych zmian wartości zmiennej prognozowanej wokół przeciętnego poziomu lub wokół trendu tej zmiennej. W gospodarce rynkowej wynikają one z przebiegu cyklu koniunkturalnego. Są to takie zmiany, które powtarzają się regularnie w analogicznych jednostkach czasu.

4. TENDENCJA ROZWOJOWA - TREND (T): przedstawia regularne i systematyczne zmiany, jakim podlega zjawisko w ciągu długiego czasu. Wyznacza rozwój zjawiska w czasie.

11. Podstawowe mierniki ex-post.

Mierniki ex-post cechują się tym, że są obliczane na podstawie materiałów z przeszłości, a więc na podstawie informacji o prognozach już wygasłych i odpowiadającej im realizacji zmiennej prognozowanej. Wśród tych mierników najczęściej oblicza się średnią arytmetyczną błędów prognozy, zwaną błędem przeciętnym (SABP).

Błąd prognozy może być równy zeru, gdy predykcja nie jest obciążona. Odchylenia dodatnie i ujemne wzajemnie się znoszą. Aby obliczyć o ile sformułowane prognozy w poszczególnych okresach różnią się średnio od rzeczywistej wartości zmiennej prognozowanej, przyjmuje się nie rzeczywiste wartości odchyleń, a ich wartości bezwzględne:

(SBWBP) = średnia bezwzględnej wartości błędów prognoz, zwana błędem prognozy.

SBWBP informuje, o ile przeciętnie odchylają się sformułowane prognozy od wartości rzeczywistej.

Miarami częściej używanymi i lepiej opracowanymi matematycznie są:

• średni kwadrat błędów prognoz (SKBP)

• standardowy błąd prognozy (SBP)

SKBP silniej reaguje na większe różnice między prognozami a wartościami rzeczywistymi.

Obliczając pierwiastek kwadratowy ze średniego kwadratu błędu, otrzymuje się odchylenie standardowe błędów prognoz (OSBP). Jest ono również nazywane empirycznym średnim błędem predykcji. Jest on najczęściej większy niż średnia bezwzględnej wartości błędów prognoz (SBWBP), ponieważ silniej reaguje na większe różnice między wartościami rzeczywistymi a sformułowanymi prognozami.

Inne błędy prognoz mogą być obliczane w wielkościach względnych, procentach. W tej klasie używa się najczęściej następujących mierników oceny dokładności prognoz:

BWP - błąd względny procentowy

SAWBP - średnia arytmetyczna względnych błędów prognoz.

12. W jakich sytuacjach można stosować do prognozowania modele średniej ruchomej?

Jednym z najprostszych sposobów zbudowania prognozy jest zbudowanie jej na podstawie średniej ruchomej (jedna z metod adaptacyjnych). W tej metodzie za prognozę przyjmuje się średnią z określonej liczby poprzednich okresów.

W tej metodzie prognozowania próbuje się wygładzić przez uśrednianie wahania przypadkowe (I). Stosowana jest dla zjawisk i procesów gospodarczych, w których nie występuje tendencja, wahania cykliczne i sezonowe. Można jej np. użyć by zbadać kształtowanie się plonów ziemniaków w latach jakichś tam.

Wada: nadaje jednakowe wagi dla wszystkich informacji. A dla wielu procesów gosp. Ważniejsze są nowsze, bardziej aktualne obserwacje niż te starsze.

Rozwiązanie: średnia ruchoma ważona: prognozę tę metodą buduje się uwzględniając tzw. Postarzanie informacji. Czyli, że informacje starsze mają relatywnie mniejsza wagę niż informacje bliższe okresowi prognozowania.

13. Jak budujemy prognozy na podstawie stacjonarnych szeregów czasowych:

Dla wielu zjawisk i procesów gospodarczych występujące zmiany nie wykazują tendencji, wahań sezonowych ani cyklicznych. Zmienność która występuje odbywa się wokół stałej wielkości. Tego typu szeregi nazywamy stacjonarnymi. Najczęściej występują z powodu:

• Ustabilizowanego otoczenia, w którym funkcjonuje dane zjawisko

• Braku postępu w danej dziedzinie

• Krótkiego horyzontu prognozy

• Początkowego etapu rozwoju danego zjawiska

Występowanie stacjonarnych szeregów czasowych powoduje konieczność zastosowania określonego sposobu budowy prognoz. Budowa prognoz oparta jest na modelu błądzenia losowego:

Y = β + ε

Gdzie:

Y - poziom zjawiska

β - średni poziom

ε - składnik losowy

KRYTERIUM I:

Suma błędów prognoz = 0

Przy powtarzaniu prognoz suma ich błędów powinna być równa zero. Za prognozę przyjmuje się wartość średniej arytmetycznej.

KRYTERIUM II:

Tak samo często niedoszacować jak i przeszacować prognozę. Wartości empiryczne należy uporządkować rosnąco, a za prognozę przyjmuje się wartość środkową.

KRYTERIUM III:

„ minimaks” - najmniejszy maksymalny błąd. Prognoza: średnia obliczona z wartości najniższej i najwyższej.

KRYTERIUM IV:

Minimalizacja błędu. Prognoza: średnia z wartości środkowych uporządkowanych rosnąco.

KRYTERIUM V:

Minimum sumy kwadratów błędów. Kryterium to spełnia średnia arytmetyczna.

14. Scharakteryzuj metodę heurystyczną:

Polega na szacowaniu różnych postaci analitycznych funkcji trendu i wyborze jednej z nich na podstawie wyróżnionego kryterium dopasowania modelu do rzeczywistości:

• Współczynnik determinacji - należy do przedziału (0, 1) przy czym wyższa jego wartość świadczy o lepszym dopasowaniu modelu. Informuje jaką część całkowitej zmienności zmiennej wyjaśnia model.

• Współczynnik zbieżności - informuje jaka część całkowitej zmienności zmiennych nie została wyjaśniona przez model. Wybieramy z oszacowanych modeli tę funkcję dla której współczynnik ten jest najmniejszy.

• Współczynnik korelacji - określa siłę związku liniowego zmiennej objaśnianej ze wszystkimi zmiennymi objaśniającymi modelu. Należy do przedziału <-1, 1 > przy czym im jest wyższy tym silniejszy związek - silniej cechy wpływają na siebie.

15. Podaj narzędzia weryfikacji modelu prognostycznego

WERYFIKACJA MERYTORYCZNA:

W ocenie tej należy zwrócić uwagę czy:

• otrzymane wyniki potwierdzają teoretyczne rozważania o objaśnianym zjawisku, czy są zgodne z teorią

• zwrócić uwagę na znaki ocen parametrów strukturalnych, czy negatywny lub pozytywny znak spełnia oczekiwania co do kierunku wpływu zmiennej objaśniającej na zmienną objaśnianą wynikającej z naszej wiedzy lub analizy.

WERYFIKACJA STATYSTYCZNA:

Prawie nigdy nie zachodzi w praktyce przypadek całkowitej zgodności wartości zaobserwowanej zmiennej prognozowanej z jej wartościami wynikającymi z oszacowanej funkcji.

Ma na celu sprawdzenie:

• stopnia przylegania modelu do opisywanego fragmentu rzeczywistości

• zestawu zmiennych objaśniających z punktu widzenia ich wpływu na zmienną objaśnianą

• rozkładu składnika losowego

NARZĘDZIA:

1. Analiza rozkładu reszt: różnice między wartościami empirycznymi a teoretycznymi zmiennej

2. Współczynnik determinacji i skorygowany: określa stopień dopasowania modelu do danych empirycznych. Im wyższa jego wartość tym model jest lepiej dopasowany. Informuje jaka część całkowitej zmienności zmiennej prognozowanej wyjaśnia model.

3. Odchylenie standardowe reszt: informuje o przeciętnych odchyleniach zaobserwowanych wartości rzeczywistych zmiennej prognozowanej od wartości teoretycznych wyznaczonych z modelu. Im mniejsze tym model lepiej dopasowany.

4. Badanie losowości odchyleń: ma na celu weryfikację hipotezy o trafności doboru postaci analitycznej modelu. Wykonujemy test serii. Losowość odchyleń oznacza że ciąg reszt powinien mieć charakter przypadkowy.

5. Badanie stacjonarności składnika resztowego: oblicza się współczynnik korelacji między odchyleniami a czasem t.

16. Wymień etapy budowy prognoz dla szeregów czasowych zawierających T, C, S, I. (w skrypcie jest tylko dla multiplikatywnego. Addytywny to moje przypuszczenia, które mogą nie być słuszne)

Opis danego szeregu czasowego może być przedstawiony przez model addytywny (suma) Albo jako model multiplikatywny ( iloczyn)

Aby zbudować prognozę na podstawie szeregu czasowego, zawierającego T, C, S ,I, musimy:

1. Dla ustalonej liczby naturalnej l >1 obliczamy kolejne wartości średniej ruchomej. Długość średniej ruchomej powinna być równa liczbie wyodrębnionych okresów, czyli gdy analiza jest robiona w kwartałach, to l = 4 razy x ( x ∈ N), gdy w miesiącach, to l = 12 razy x itd. ( Metoda średnich ruchomych należy do mechanicznych sposobów wyodrębniania T, a scentrowane średnie ruchome SRc = Tt Ct )

2. Wyodrębniamy z szeregu wahania sezonowe. W przypadku opisu szeregu czasowego modelem addytywnym, od wartości empirycznych należy odjąć odpowiadające im obliczone średnie ruchome.

Y t= Tt+ St + It - SR= St + It

Gdy model jest multiplikatywny, to sezonowość obliczamy, dzieląc wartości empiryczne przez odpowiadające im średnie ruchome

Y t= Tt St It / Tt Ct = St It

3. dokonujemy odpowiedniej korekty otrzymanych surowych wskaźników wahań sezonowych i otrzymujemy czyste wahania sezonowe.

4. Eliminujemy z szeregu sezonowości S: w modelu addytywnym odejmujemy od wartości rzeczywistych Yt czyste wahania sezonowe St

Y t= Tt+Ct +St + It - St = Tt + Ct + It - otrzymujemy szereg czasowy bez wahań sezonowych

W modelu multiplikatywnym dzielimy przez St

Y t= Tt Ct St It / St = Tt Ct It

5. obliczmy funkcję trendu najlepiej opisującą szereg czasowy po wyrzuceniu sezonowości. Mamy do wyboru f. Liniową, wykładniczą, potęgowa i hiperboliczną.

(W przypadku modelu addytywnego od wart. Empirycznych Yt

Yt - ( Tt + S) = Tt + St + It - Tt - St = It.

W przypadku multiplikatywnego dzielimy )

6. Wyodrębniamy wahania cykliczne C : w modelu addytywnym odejmujemy od wartości średniej ruchomej średni poziom w danych latach. W modelu multiplikatywnym dzielimy wartości średniej ruchomej przez średni poziom w latach

SR Tt Ct

= = Ct

Tt Tt

7. Wyodrębniamy wahania przypadkowe (It): w modelu addytywnym odejmujemy od wartości po wyeliminowaniu sezonowości średnia ruchomą

Tt + Ct + It - SR = It

W multiplikatywnym wartości po usunięciu sezonowości dzielimy przez SR

Tt Ct It

= It

SR

8. W ten sposób wyodrębniliśmy wszystkie elementy szeregu czasowego . Mając je możemy zbudować prognozę przez ekstrapolacje funkcji trendu. Uzyskujemy poziom zjawiska bez S i C, należy je uwzględnić, dodając je do wartości uzyskanych z ekstrapolacji (m. addytywny) lub mnożąc (multiplikatywny)

9. Wyboru, czy ma być to model addytywny czy multiplikatywny najlepiej dokonać w Statgraphicsie.

17. W jaki sposób eliminujemy z szeregu wahania sezonowe?

1. Dla ustalonej liczby naturalnej l >1 obliczamy kolejne wartości średniej ruchomej. Długość średniej ruchomej powinna być równa liczbie wyodrębnionych okresów, czyli gdy analiza jest robiona w kwartałach, to l = 4 razy x ( x ∈ N), gdy w miesiącach, to l = 12 razy x itd. ( Metoda średnich ruchomych należy do mechanicznych sposobów wyodrębniania T, a scentrowane średnie ruchome SRc = Tt Ct )

2. Wyodrębniamy z szeregu wahania sezonowe.

W przypadku opisu szeregu czasowego modelem addytywnym, od wartości empirycznych należy odjąć odpowiadające im obliczone średnie ruchome.

Y t= Tt+ St + It - SR= St + It

Gdy model jest multiplikatywny, to sezonowość obliczamy, dzieląc wartości empiryczne przez odpowiadające im średnie ruchome

Y t= Tt St It / Tt Ct = St It

3. Dokonujemy odpowiedniej korekty otrzymanych surowych wskaźników wahań sezonowych i otrzymujemy czyste wahania sezonowe.

4. Eliminujemy z szeregu sezonowości S: w modelu addytywnym odejmujemy od wartości rzeczywistych Yt czyste wahania sezonowe St

Y t= Tt+Ct +St + It - St = Tt + Ct + It - otrzymujemy szereg czasowy bez wahań sezonowych

W modelu multiplikatywnym dzielimy przez St

Y t= Tt Ct St It / St = Tt Ct It

To tyle. Potem jeszcze e) obliczmy funkcję trendu najlepiej opisującą szereg czasowy po wyrzuceniu sezonowości. Mamy do wyboru f. Liniową, wykładniczą, potęgowa i hiperboliczną. )

18. Podaj technikę wyodrębniania i eliminacji z szeregu czasowego tendencji rozwojowej.

Podstawą do wyodrębnienia tendencji rozwojowej danego zjawiska jest szereg czasowy po wyeliminowaniu wahań sezonowych. W tym celu na podstawie danych oblicza się funkcję trendu opisującego tendencję.

Otrzymujemy obliczoną funkcję trendu.

Teraz można obliczyc wartości liczbowe charakteryzujące tendencje ( Tt ). Jest to kolejny elelment szeregu czasowego.

W przypadku modelu addytywnego od wartości empirycznych Yt odejmuje się opisane elementy

Yt - ( Tt + S) = Tt + St + It - Tt - St = It

W multiplikatywnym dzielimy wartości empiryczne przez opisane elementy.

Yt Tt St It

= = It

Tt St Tt St

19. Co wiesz o dekompozycji szeregu czasowego?

Dekompozycja szeregu czasowego to wyodrębnienie elementów występujących w szeregu czasowym. Służy ona do zbudowania prognozy. Dekompozycja szeregu czasowego pozwala bowiem wyodrębnić i opisać zarówno te elementy szeregu, które mogą być przewidziane, jak i te, których nie można przewidzieć (wahania przypadkowe, nieregularne)

W przypadku, gdy w szeregu czasowym występuje: T, S I, dekompozycję przeprowadzamy tak: ( wyżej opisane szczegółowo)

1. Obliczamy wielkość wahań sezonowych

2. Eliminujemy S z szeregu czasowego

3. Obliczamy f,trendu na podstawie szeregu po wyrzuceniu S

A potem już tylko budujemy prognozę metodą ekstrapolacji f. Trendu i obliczamy prognozy dla poszczególnych okresów.

20. Wymień znane ci adaptacyjne metody prognozowania:

Wyróżniamy:

• Metoda średniej ruchomej

• Metoda średniej ruchomej ważonej

• Model wyrównywania wykładniczego Browna rzędu I, II i III

• Model wyrównywania liniowo - wykładniczego Holta

• Model wyrównywania wykładniczego Wintersa

• Model trendu pełzającego z wagami harmonicznymi

21. Co wiesz o prognozowaniu metodą wyrównywania wykładniczego Holta:

• podobna do Browna II rzędu

• występują dwie stałe wygładzania: α - do wygładzania poziomu trendu; γ - do wygładzania jego zmian

• ważny jest wybór stałych wygładzania - dokonuje się tego z punktu widzenia minimalizacji błędów sporządzonych prognoz

• nadaje się do prognozowania szeregu z tendencją rozwojową i wahaniami przypadkowymi

• należy do adaptacyjnych metod prognozowania

22. Jakie znasz heurystyczne metody prognozowania i wymień etapy postępowania w metodzie delfickiej.

Heurystyczne (intuicyjne) metody prognozowania są szeroko rozpowszechnione w teorii i praktyce prognostycznej. Opierają się one na wyobraźni i zdrowym rozsądku. Z reguły te metody nie są oparte na ścisłych obliczeniach i nie dają się przedstawić za pomocą modelu matematycznego.

Ogólną ideą prognozowania tymi metodami jest porządkowanie wypowiedzi i ocen ekspertów z danej dziedziny wiedzy dotyczącej przyszłości, dlatego metody heurystyczne w dużym stopniu opierają się na opiniach i intuicji badawczej specjalistów. Dlatego dobór ekspertów jest bardzo ważny.

Wyróżniamy metodę indywidualnych ekspertyz (ocen rzeczoznawców) oraz metodę ekspertyz zespołowych (równoległych lub kolejnych), którą dzielimy na

• metodę delficką

• metodę SEER ( system for event evaluation and review)

• burzę mózgów

• buzz sesion

• metode kolektywnego generowania pomysłów

• synektykę

• metodę wpływów krzyżowych ( cross- impact matrics)

METODA DELFICKA to jedna z odmian ekspertyz zespołowych. Zyskała duży rozgłos i jest powszechnie stosowana. Prognozowanie tą metoda polega na opracowaniu szczegółowych ankiet skierowanych do specjalistów i ekspertów, a następnie na uogólnieniu opinii na podstawie statystycznej analizy uzyskanych odpowiedzi.

Etapy:

• opracowanie kwestionariuszy prze organ kierujący badaniami

• przekazanie kwestionariuszy ekspertom, którzy są kompetentni w swoich dziedzinach

• uzyskanie odpowiedzi

• zebranie i usystematyzowanie opinii

• Jeżeli zgoda nie została osiągnięta, to następuje ponowne sformułowanie pytań i przekazanie ich wraz z wynikami z pierwszej rundy badań do oceny specjalistów

• otrzymanie kwestionariuszy w drugiej turze ankietowania

• zebranie i statystyczna analiza uzyskanego materiału

• jeżeli zgoda została osiągnięta, to następuje ogłoszenie wyników

• jeżeli zgoda nie została osiągnięta, to ankiety rozsyłane są jeszcze raz itd...

Metoda cechuje się niezależnością opinii ekspertów, anonimowością sądów, wieloetapowością postępowania, uzgadnianiem i sumowaniem opinii osób kompetentnych. Zwykle prognozą jest opinia większości zgodnych uczestników badania.

23. Wymień analogowe metody prognozowania i omów wariant wzorca.

• analogii biologicznych

• analogii przestrzennych

• analogii historycznych

• analogii przestrzenno-czasowych

• trendów prekursywnych i współwiązanych

WARIANT WZORCA - polega na naśladowaniu procesów zachodzących w krajach, regionach lub obiektach wyżej rozwiniętych przez kraje, regiony lub obiekty opracowujące prognozę. Praktycznie sprowadza się to do odnalezienia w historii kraju, regionu lub obiektu lepiej rozwiniętego, przyjmowanego jako wzorzec, poziomu rozwoju zjawiska, jaki występuje w obiekcie sporządzającym prognozę.

24. Wymień znane Ci funkcje prognoz i omów jedną z nich

• POZNAWCZA (ROZPOZNAWCZA, INFORMACYJNA) prognozy sporządza się, aby na ich podstawie wyznaczyć realne cele i warunki w których będą działały. Z niej można dowiedzieć się o tendencjach rozwojowych badanych zjawisk i procesów, wpływu na nie różnych czynników, siły i rodzaju współzależności między procesami, możliwościach i ograniczeniach rozwojowych.

• DECYZYJNA (PREPARACYJNA) w większości wypadków prognozy sporządza się w celu uzyskania określonych informacji niezbędnych do przygotowania i podejmowania decyzji. Prognozowanie jest działaniem, które przygotowuje inne działania.

• STRATEGICZNA prognozy mogą stanowić podstawę długofalowego działania lub długofalowej polityki gospodarczej.

• OSTRZEGAWCZA mogą dostarczać także na czas informacji o ewentualnej niekorzystnej zmianie kierunku czy natężenia badanego zjawiska, jakie może wystąpić w przyszłości. Celem tej funkcji jest możliwość podjęcia działań zapobiegaczo - preferencyjnych w odpowiednim czasie.

• WERYFIKACYJNA w wyniku takich prognoz mamy rozpoznanie co do stopnia realizacji wcześniej założonych zadań.

• AKTYWIZUJĄCA prognozy mogą odnosić się do różnych zmiennych na które decydent ma wpływ lub nie ma. Funkcja prognozy polega na pobudzeniu do podejmowania działań sprzyjających realizacji prognozy gdy zapowiada ona zdarzenie korzystne i przeciwstawiających się jej realizacji gdy przewidywane zdarzenia są oceniane jako niekorzystne.

25. Co wiesz o prognozowaniu metodą Wintersa?

Jest to jedna z adaptacyjnych metod prognozowania. Stosuje się ją gdy w szeregu czasowym występują wahania sezonowe i tendencja.

Występują 3 stałe wygładzania:

α - do wygładzania poziomu trendu

γ - do wygładzania zmiany trendu

δ - do wygładzania wahań sezonowych

Wybieramy tą z najmniejszym średnim kwadratem błędu prognoz.

26. Co wiesz o metodach prognozowania koniunktury gospodarczej?

Do metod prognozowania koniunktury gospodarczej należą:

Metoda zmiennych wiodących badania wykazują że są takie rodzaje zmiennych, które wcześniej sygnalizują nadchodzące wydarzenia. Punktem wyjścia do prognozowania tą metodą jest wybór takiej zmiennej, która charakteryzuje główne zmiany w gospodarce - nosi ona nazwę zmiennej referencyjnej najlepiej gdy jest nią produkt krajowy czasami zastępuje się go inną kategorią np.: produkcja przemysłową. Analizując w czasie inne zmienne i odnosząc je do zmian zmiennej referencyjnej, wyodrębnia się trzy grupy zmiennych: wiodące - doświadczają faz cyklu koniunkturalnego wcześniej niż zmienne referencyjne, zbieżne - przechodzą fazy cyklu koniunkturalnego wraz ze zmiennymi referencyjnymi, naśladujące - przechodzą fazy cyklu koniunkturalnego później niż zmienne referencyjne.

Metoda testu koniunktury

Cel: określenie aktualnego poziomu aktywności gospodarczej - opracowany na podstawie ankiet.

Pytania w ankiecie do grupy:

1. diagnostyczne - przeszłość i stan aktualny

2. przyszłości, oczekiwania i różnego rodzaju planów

3. specjalne - zadawanie sporadycznie np.: czas pracy, zatrudnienia

4. dodatkowe

Mając wyniki należy ocenić różne warianty: stan normalny, stan wzrostu - ocena polepszenia, stan spadku. Następnie opracowanie pytań (IRG i GUS) - uzyskujemy informacje dotyczącą stanu poprzedniego - konstruuje się wskaźnik koniunktury.

27. Prognozy ostrzegawcze - pojęcie i sposoby.

Prognozy ostrzegawcze dostarczają na czas informacji o ewentualnie niekorzystnej zmianie kierunku czy natężenia badanego zjawiska, jakie może wystąpić w przyszłości. Zmienne dzielimy na trzy grupy:

Stymulanty - ich wzrost świadczy o pożądanym kierunku rozwoju

Destymulanty - ich spadek świadczy o pożądanym kierunku rozwoju

Nominanty - charakteryzują się pewnym poziomem nasycenia, od którego odchylenia uznaje się za niepożądane.

Mając 3 grupy zmiennych konstruujemy prognozę:

Metoda konstrukcji punktów ostrzegawczych:

• analiza tendencji 3 zmiennych: załamanie trendu spadkowego w przypadku destymulant, załamanie trendu rosnącego w przypadku stymulanty,

• wykorzystanie kart jakości

• analiza cyklów koniunktury - ostrzeganie przed nadejściem określonej fazy cyklu koniunktury.

28. W jakich sytuacjach możemy stosować do prognozowania modele średniej ruchomej?

Metoda średniej ruchomej stosowana jest dla zjawisk i procesów gospodarczych w których nie występuje tendencja, wahania sezonowe i cykliczne.

W tej metodzie za prognozę przyjmuje średnią z określonej liczby poprzednich okresów. Liczba uwzględnionych okresów określa długość średniej ruchomej która oblicza się ze wzoru.


Ŷ_t+p=[Y_t+Y_t-1+...+Y_t-L+1]/L

Ŷ_t+p - prognoza dla t+p okresów

Y_t- wartość zmiennej prognozowanej

L- liczba obserwacji

p - odległość okresu prognozowanego od t (p>1)

Dzięki tej procedurze staramy się staramy się „wyrównać , wygładzić” przez uśrednianie wahania, przypadkowe nieregularne.

Bardzo ważne jest aby przyjąć taką długość średniej ruchomej (l) przy której błąd prognozy jest najniższy. Im średnia ruchoma dłuższa tym większe wygładzanie , ale średnia wolniej reaguje na zmiany poziomu prognozowanej zmiennej.

29. Prognozowanie na podstawie ekstrapolacji funkcji trendu.

Ekstrapolacja w statystyce wnioskowanie o wartościach całego zbioru na podstawie badań wyników jego części,

W celu wykorzystania obliczonej funkcji trendu do oszacowania prawdopodob­nego poziomu zjawiska w przyszłości przyjmuje się założenia teorii predykcji, zgodnie z którymi będzie budowana prognoza.

Przyszłą wartość prognozowanego zjawiska uzyskuje się przez ekstrapolację funkcji trendu, to jest podstawienie do modelu w miejsce zmiennej czasowej numeru okresu do którego odnosi się prognoza.

Sposób budowy prognozy punktowej i przedziałowej przedstawiono na przy­kładzie funkcji trendu liniowego. Wzory i sposób postępowania można także wyko­rzystać w przypadku funkcji nieliniowych, poddających się transformacji liniowej (funkcja hiperboliczna, potęgowa, wykładnicza).

Prognozę punktową metodą ekstrapolacji funkcji trendu prostoliniowego otrzy­muje się zgodnie ze wzorem:

Ŷ_t+p=β₀+β_1(t+p)

Ŷ_t+p - prognoza punktowa w okresie t+p

p- odległość okresu prognozowanego od t

β_o,β₁- parametry funkcji trendu

Tak wyznaczoną wielkość określa się mianem prognozy punktowej. Do oceny jej jakości używa się bezwzględnego błędu prognozy ex ante, który w przypadku liniowej funkcji trendu określony jest wzorem:


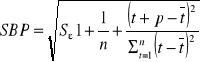
(1)

Sε - odchylenie standardowe składnika resztkowego,

n - długość szeregu t= 1, 2,..., n.

Często, oprócz wyznaczania prognozy punktowej, konstruuje się przedział prognozy (prognozę przedziałową), to jest przedział liczbowy, do którego z góry zadanym prawdopodobieństwem (p), zwanym wiarygodnością prognozy, należeć będzie przyszła wielkość zmiennej prognozowanej. Przyjęcie tej zasady prognozo­wania wynika ze zmienności występującej w szeregu czasowym (odchylenia przy­padkowe). Istnieje wiele sposobów budowy przedziału prognozy

Prognozę przedziałową, przy współczynniku ufności 1 - α dla funkcji prostoli­niowej, buduje się według wzoru:

P{Ŷ_t+p - t_α SBP < Y_t+p < Ŷ_t+p + t_α SBP}=1-α (2)

P=1-α prawdopodobieństwo.

Ŷ_t+p - prognoza punktowa wartości Ŷ_t+p

SBP- błąd średni (standardowy) prognozy,

t_α- wartość zmiennej t - studenta odczytana z tablicy dla n - k -1 stopni swobody i przyjętego współczynnika ufności 1 - α.

W przypadku regresji prostoliniowej z jedną zmienną objaśniającą (t) błąd średni (standardowy) prognozy oblicza się zgodnie ze wzorem (1)

Z właściwości i warunków stosowania metody ekstrapolacji wynika, że najle­psze rezultaty uzyskuje się w odniesieniu do zjawisk jednorodnych, o przewadze elementów ilościowych, gdy zjawiska lub procesy gospodarcze nie podlegają zna­cznym zmianom strukturalnym.

30. Podaj sposób wyodrębniania z szeregu czasowego wahań cyklicznych i sezonowych.

Przede wszystkim należy obliczyć średnią ruchomą (SR) długości L równej liczbie wyodrębnionych okresów.

SR=T_t•C_t

T_t - wartość poziomu trendu w okresie t

C_t - wahania cykliczne w okresie t

Aby wyodrębnić z szeregu wahania sezonowe należy wartości empiryczne podzielić przez średnią ruchomą.

Y_t/SR=C_t•T_t•I_t•S_t/C_t•T_t => I_t•S_t => jest to surowy wskaźnik wahań sezonowych

Należy dokonać odpowiedniej korekty surowych wskaźników, by Σ S_t=L(liczbie okresów), aby tak się stało należy I_t•S_t podzielić przez współczynnik korekty a.




Następnie eliminuje się z szeregu czasowego wahania sezonowe przez podzielenie wartości empirycznych (Y_t), przez wskaźnik korekty.

Y_t/S_t=C_t•T_t•I_t•S_t/S_t => C_t•T_t•I_t

31. Zadanie: znając kwartalne addytywne efekty sezonowe sprzedaży konserw: I=0,825, II=2,525, IV= -4,675 ; wyznacz i zinterpretuj efekt sezonowy w III kwartale.

I + II + III + IV = 0

0,825 + 2,525 + III - 4,675 = 0

3,35 - 4,675 = - III

-1,325 = - III

III = 1,325 - efekt sezonowy w III kwartale

32. Jak graficznie zidentyfikować T C S / Na podstawie wzrokowej oceny szeregów czasowych dokonaj wstępnej identyfikacji elementów szeregu czasowego (ogólnie bo nie mamy wykresu).

(S)- wahania sezonowe są to zmiany powtarzające się regularnie w tym samym okresie każdego roku wokół stałego poziomu lub trendu zmiennej. Wynikają z zachowań ludzkich ( pór roku świąt ) lub specyfiki i charakteru produkcji.

(T)- tendencja rozwojowa wyznacza rozwój zjawiska w czasie, przedstawia regularne i systematyczne zmiany, jakim podlega zjawisko i w ciągu długiego czasu.

(C) wahania cykliczne długookresowe rytmiczne wartości zmiennej prognozowane wokół przeciętnego poziomu lub trendu tej zmiennej ( cykle świńskie lub bydlęce - pogłowie zależy od ceny ).

Przykładowe szeregi czasowe




Wahania przypadkowe wokół średniej.




Wahania przypadkowe i trend.




Wahania sezonowe i przypadkowe wokół średniej




Trend wahania sezonowe i przypadkowe




Wahania cykliczne wokół średniego poziomu




Trend wahania przypadkowe sezonowe cykliczne

2

---