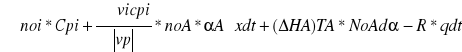
w izotermie - gdy temperatura w całej objętości reaktora jest stała T1=T![]()
szybkość jest uzależniona od stopnia przemiany w praktyce najwygodniej jest realizować w produkcję za pomocą układu regulującego dopływ pary grzejnej za pomocą czujnika umieszczonego w masie reakcji .
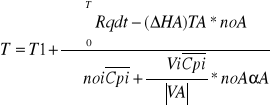
Adiabatyczne- warunki w których nie zachodzi wymiana ciepła z otoczeniem. Zatem podwyższenie temperatury jest konsekwencją ciepła reakcji egzotermicznej. Jeżeli w tych warunkach wymiana ciepła nie zachodzi to: 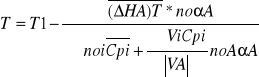
Lub po wprowadzeniu średniej entalpii reakcji T1-T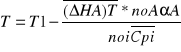
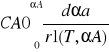
VmR=const
t= 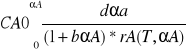
VmR![]()
const
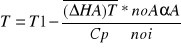
![]()
to pełny matematyczny adiabatycznego reaktora okresowego, w/w rozwiązaniu otrzymuje się z bilansu masowego n
![]()
![]()
proces nie izotermiczny ze stałą szybkością wymiany cieplnej Rq=const jeśli istnieje duża różnica temperatur między czynnikiem grzejnym chłodzącym a mieszaniną reakcyjna.
Tq-T=const
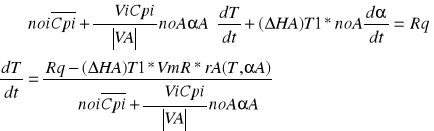
lub po wprowadzeniu średniej entalpii molowej 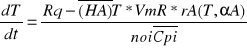
T=f(t)
Wcześniejsze równania uzyskuje się pełny model określonego reaktora nie izotermicznego ze stałą wymianą ciepła.
Proces nie izotermiczny ze zmienną szybkością wymiany ciepła
W przypadku przeponowego ogrzewania mieszaniny reakcyjnej za pomocą pary grzejnej przy czym mieszanina jest intensywnie mieszana K,F,Tq =const T=f(t) Tq-T![]()
const Powyższe równania przyjmują formę 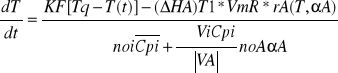
lub po wprowadzeniu średniej entalpii uzyskuje się 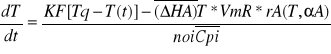
Reaktory przepływowe
Rurowy- wieżowy
Dla reaktora rurowego - przepływ tłokowy nie następuje tu gradient stężenia i temperatury: konstrukcja taka gwarantuje szybkość reakcji i stosunkowo krótki czas przebywania. Z punktu widzenia modelu matematycznego rozróżnia się następujące modele: 1-wymiarowy o przepływie tłokowym, 1-wymiaroym o przepływie dyspersyjnym, 2-wymiarowy jednoparametrowy, 2-wymiarowy dwuparametrowy, r-rurowe wykonuje się do prowadzenia procesu w fazie gazowej i ciekłej. W wyniku istnienia gradientu stężenia i temperatury w kierunku przepływu najczęściej rozpatruje się 1-wymiarowy o przepływie tłokowym lub dyspersyjnym
![]()
w idealnym reaktorze przepływowym
AR*U*CA strumień wejściowy
AR*U*CA-RA*U(CA+dCA/dxdx)+-AR*rA(T,CA)dx=0 ogólne równanie masowe reaktora okresowego. Po uproszczeniu mamy -UdCA/dx=rA(T,CA)
AR-przekrój poprzeczny reaktora
Po wprowadzeniu stopnia przemiany dogodnie z def oraz bezwymiarowej długości reaktora αA=CA0-CA/CA0
l=x/L e(0,1)
CA0=dCA/dt=V*rA(αA,T)
Równanie projektowe reaktora rurrowowężowego
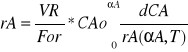
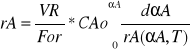
AR=const VR-AR*x Objętość reaktora rurowego
DVR=AR*dx
Bilans cieplny
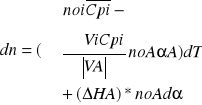
dn/dt=0 równanie bilansu cieplnego sprowadza się do postaci
![]()
różniczka entalpii
![]()
w ilość ciepla wymieniona z otoczeniem
dh =dQw
dh=Rqv*dvR
rqv=kt(Tq-T) określa powierzchnię wymianę ciepła w odniesieniu do metra sześciennego objętości reaktora
RqvdVR=AR*Rv*dx=(Rgl)x
Fv- powierzchnia wymiany ciepła odniesiona do 1 metra sześciennego odniesiona do reaktora
Fx- powierzchnia wymiany ciepła odniesiona do 1 metra bieżącego długości reaktora
Uzyskuje się ogólne równanie bilansu cieplnego reaktora rurowego
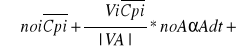
+(ΔHa)nCA*dαA=Rqv*dVR
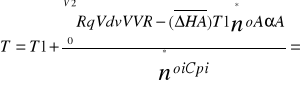
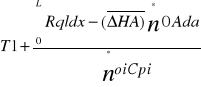
Proces izotermiczny - w procesie tym model reaktora stanowi jedyne równanie bilansu materiałowego które w postaci całkowitej przyjmuje postać
CA0=![]()
l=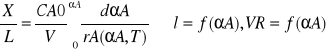
αA=f*(l)
w wyniku rozwiązania uzyskuje się rozkład stopnia przemiany wzdłuż długości reaktora
l=x/L - całkowita długość reaktora
Kumulujące się w/w reakcji ciepło zostaje odbierane w przypadku reakcji egzotermicznej przez czynnik zewnętrzny. Zaś szybkość tej przemiany określa równanie
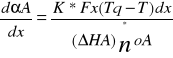
to równanie określa zmianę stopnia przemiany wzdłuż długości reaktora x, przy wymianie ciepła z otoczeniem
Proces adiabatyczny - w procesie tym ciepło Rqv =0 zatem model reaktora rurowego określa równanie bilansu materiałowego oraz równie bilansu cieplnego w postaci (brak wymiany ciepła z otoczeniem)
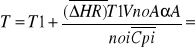
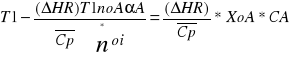
Jak wynika z układu rozkład temperatur jest liniową funkcją stopnia przemiany
Cw=ρ/kgK
Cw=Cp/N
Cp=J/molK
Proces nie izotermiczny ze stałą szybkością wymiany ciepła RqL=const. Model tego procesu opisuje równanie bilansu materiałowego odniesione do objętości reaktora oraz równanie bilansu cieplnego przy założeniu RqV=const
Rownanie bilansu materiałowego dαA/dVR=Ra(αA,T)/noA oraz równanie bilansu cieplnego które uzyskujemy uwzględniając w ogólnym równaniu
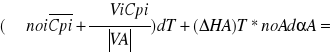
![]()
przyjmujemy średnice molowe ciepła ![]()
![]()
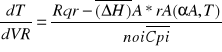
Proces nie izotermiczny ze zmienną szybkością wymiany ciepła RqL![]()
const
![]()
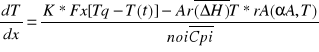
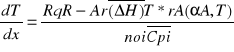
Reaktor zbiornikowy: W reaktorze tym świeży strumień surowca miesza się z całą objętością mieszaniny reakcyjnej według wzoru czego następuje spadek stężenia substratów i w konsekwencji zmniejszenie szybkości. Reaktory charakteryzują się dużą średnicą w stosunku do ich długości (nierzadko są to reaktory kuliste). Zaopatrzone zazwyczaj w urządzenie mieszające utrzymujące stan zbliżony do stanu idealnego wymieszania, a w konsekwencji nie występują gradienty stężenia i temperatury. Zaletą ich są łatwość utrzymywania warunków izotermicznych ze względu na zbyt małą powierzchnię wymiany ciepła w porównaniu z ich objętością. Stosowane do prowadzenia w fazie ciekłej pod niskim lub średnim ciśnieniem. Mogą być też stosowane w reakcjach o silnym efekcie termicznym pod warunkiem że poziom temperatury jest dogodny za względu na inne okoliczności. Wadą jest to że nie nadają się do prowadzenia reakcji w fazie gazowej oraz mała szybkość zachodzących przemian. Równanie projektowe (bilansu materiałowego) zakładamy że akumulacja równa się 0. dn/dt=0
Przyrost liczby moli ΔnA=RAszybkość reakcji
![]()
różnice strumieni z definicji stopnia przemiany mamy Δna=noa (α2A-α1A)=Fonxox(α2A-α1A)For*CoA(α2A-α1A)
Z=VR/Fon=xox(α2A-α1A)/rA(α2A)
Z'=VR/Fon=CoA(α2A-α1A)/rA(αoA)
Strumień liczby moli przepływającego składnika Noa=ForCoA=FonxoA
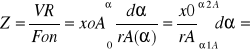
![]()
kaskada reaktorów zbiornikowych :
równanie projektowe- w wielu przypadkach korzystne jest stosowanie zespołu mniejszych reaktorów zbiornikowych zamiast jednego reaktora dużego, taki zespół w którym strumień opuszczający pierwszy reaktor...
baterie reaktorów zaopatrzony w mieszadła jest stosowany do reakcji biegnących w środowisku ciekłym. Liczbą stopni kaskady nazywa się liczbę reaktorów pracujących, w zespole reaktory kaskady mogą mieć taką samo objętość bądź mogą się nią różnić. Zastosowanie kaskady pozwala zmniejszyć stopień wady jednego reaktora. Jeżeli liczba stopni kaskady jest odpowiednio duża to końcowy stopień przemiany zbliża się do wartości osiąganych w idealnym reaktorze rurowym bądź okresowym. Równanie projektowe dowolnego reaktora kaskady przyjmuje postać identyczna jak dla reaktora pojedynczego zależnie od warunków dla reaktora n
![]()
![]()
lub ![]()
Vrm - objętość m-tego stopnia kaskady
Vm zm -zsatepczy czas przebywania w reaktorze m
αm,A stężenia bądź stopnie przemiany w reagenta A w strumieniu zasilanym
Zatem w odniesieniu do kaskady z rysunkiem modelu matematycznego przedstawia się następująco
![]()
![]()
![]()
po wprowadzeniu stopnia przemiany αmA=CoA-CmA/CmA
![]()
![]()
![]()
Wydajność kaskady zależy od liczby strumieni wielkości stopni i intensywności mieszania, najczęściej oblicza się końcowe stężenie. Szczegół I rzędu zastępczy czas przebywania. Temperatury we wszystkich stopniach są taki same, końcowe stężenie lub końcowy stopień przemiany możemy wyrazić wzorem jeżeli dane jest rA=kCA=kCAo(1-αA) to po rozwiązaniu równia ogólnego dla n-tego stopnia mamy ![]()
a stąd dla m=1
![]()
αn=0
Reaktor pół okresowy(pół przepływowy) charakteryzuje się tym że część reagenta wprowadzona jest na zas. okresowości a część zgodnie z zas. obowiązująca dla reaktora okresowego faza okresowa- faza ciekła. Faza gazowa f przepływowa. Reaktory poł przepływowe pracują w warunkach nieustalonych. Mamy trzy sposoby prowadzenia procesów w tym reaktorze:
reakcja odwracalna - gdy jeden z produktów może być odbierany na początku wprowadza się wszystkie substraty do reaktora i po zainicjowaniu reakcji i odbiera się pożądany produkt, przypadek opisuje zależność Fm=0 F2m![]()
0 np. reakcje estryfikacji w którym woda jest odprowadzana w sposób ciągły.
reakcja złożona - A+BP
A+AX w tym przypadku do reaktora ładuje się całkowitą masę substratu B, a substrat A dozuje się małymi porcjami, zachodzi tu Fm![]()
0 i F2m=0 utrzymuje się stężenie A na niskim poziomie nie dopuszczając do wzrostu produktów ubocznych np. chlorowanie benzenu
Reakcje egzotermiczne - aparat napełnia się jednym z substratów następnie w sposób ciągły podaje się porcjami drugi surowiec ten typ reakcji ma miejsce w przypadku istnienia produktów ubocznych - reakcje II typu lub przy reakcji silnie egzotermicznej.
Równanie projektowe w reaktorze takim zachodzą przemiany chemiczne spełnia zasadę zachowania masy, zatem akumulacja masy =dm/dt=F1m=F2m F1,F2m=const m=m0+(F1m-F2m)*t
ρmR=mmR/VmR,ρomR=monR/VomR
VmR=VomRρomR+(F1m-0F2m)*t/ρmR przyjmujemy że ρmr=ρomr=const to reakcja jest egzotermiczna VmR=VomR+(F1m-F2m)*t/ρmR równania te dotyczą ogólnego równania bilansowego. dnA/dt=F1mXa/Ma-F2mX2a/Ma+-VmR*rA Jeżeli w układ wchodzą równania niezależnych reakcji to wówczas obowiązuje równanie 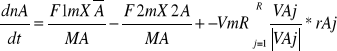
Bilans cieplny reaktora pół przepływowego wynika z bilansu masowego strumienia wpływającego i wypływającego ![]()
![]()
Wyszukiwarka
Podobne podstrony:
2372
kolo pyt i odp wszystko id 2372 Nieznany
2372
2372
2372
2372
2372
2372 Pytania egz dypl IBSN 1
Electrolux ERN 2372 Manual
2372
więcej podobnych podstron