Prognozowanie i symulacja

Wykład 3: „Prognozowanie analogowe na przykładach metod -

analogii historycznych oraz analogii przestrzenno-czasowych”

1. Istota i cechy charakterystyczne prognozowania analogowego

Pojęcie „analogia” pochodzi z języka greckiego i oznacza „podobieństwo” - rzeczy, sytuacji, procesów, które ogólnie są różne. Z tego źródłosłowia współczesna teoria „prognozowania przez analogię” rozumiana jest jako: przenoszenie wiedzy o jednym zjawisku (obiekcie) na inne zjawisko bądź zjawiska (obiekty).

Prognozowanie na podstawie analogii nie zakłada identyczności zjawisk zachodzących w analizowanych obiektach, lecz ich podobieństwo. Przy czym w procesie prognostycznym nie poddaje się głębszej analizie przyczyn występowania podobieństwa. Na takiej podstawie pełna definicja prognozowania przez analogię brzmi następująco:

„Prognozowanie przez analogię można rozumieć jako wnioskowanie o przyszłości określonego zjawiska (zmiennej) występującego w danym obiekcie, poprzez wykorzystanie informacji o kształtowaniu się tego zjawiska (zmiennej) w tym samym lub podobnych obiektach, lub też poprzez wykorzystanie informacji o innych zjawiskach (zmiennych) występujących w tym samym lub podobnych obiektach”.

Zjawisko (zmienna) prognozowane i zjawiska (zmienne) wykorzystywane do ustalenie prognozy mogą być identyczne co do swej istoty, bądź mieć różną istotę. W tym pierwszym przypadku mówi się o prognozach z użyciem zmiennych jednoimiennych. W drugim przypadku mówi się o prognozach z użyciem zmiennych różnoimiennych.

Prognozowanie zmiennych jednoimiennych ma miejsce gdy:

• Zmienna prognozowana i zmienne wykorzystywane do określania prognozy mają to samo miano, przy czym każda z nich jest funkcją czasu;

• Zmienna prognozowana i zmienne objaśniające mają te same miana w obiekcie prognozowanym i podobnym, przy czym nie są funkcjami czasu.

Prognozowanie zmiennych różnoimiennych ma miejsce wówczas gdy:

• Zmienna prognozowana i zmienne wykorzystywane do wyznaczenia prognozy mają różne miano i jednocześnie każda z nich jest funkcją czasu;

• Zmienna prognozowana i zmienne objaśniające mają różne miana i zarazem wszystkie one nie są funkcjami czasu.

Prognozowanie analogowe jest dość często stosowane w praktyce. Dlaczego? Uzasadnieniem odpowiedzi jest fakt, iż często się zdarza że pewne prawidłowości w dziedzinie zjawisk społecznych (w tym i gospodarczych) są stosunkowo mało stabilne, co uniemożliwia posługiwanie się matematyczno-statystycznymi metodami prognozowania.

Natomiast cechą charakterystyczną i okolicznością, w której powinno się stosować prognozowanie analogowe jest brak wiedzy teoretycznej dostarczającej pełnego przyczynowo-skutkowego wyjaśnienia zjawiska.

Albo też gdy badania empiryczne wykazały dużą zmienność w czasie zbierania danych o przyczynach oddziaływujących na zjawisko.

Prognozowanie analogowe to nazwa wspólna obejmująca różne rodzaje metod prognozowania. Cztery najważniejsze rodzaje metod analogowych to:

1. Metoda analogii biologicznych - polegająca na przenoszeniu wiedzy o budowie i funkcjonowaniu organizmów żywych na inne niematerialne obiekty. Przykładowo:

• konstrukcja maszyny opracowana i zbudowana na wzór budowy ciała zwierząt;

• wytwarzanie różnych rodzajów lekarstw oparte na znajomości niektórych właściwości poszczególnych roślin, itp.

2. Metoda analogii przestrzennych - polegająca na przewidywaniu zajścia konkretnego zdarzenia na danym terytorium, na podstawie informacji o wystąpieniu takiego zdarzenia na innych terytorium. Przykładowo:

• pojawienie się epidemii choroby w jednym kraju pozwala przypuszczać że wystąpienie zachorowań na innych konkretnych obszarach również będzie miało miejsce;

• wzrost popytu na posiadanie telefonów komórkowych w jednym państwie pozwala przypuszczać że podobne zjawisko wystąpi w innych państwach o nieco opóźnionym, względem tego pierwszego, rozwoju gospodarczym;

• efekty zastosowania pewnych technologii w jednym przedsiębiorstwie mogą sprawdzić się w innych przedsiębiorstwach, itp.

3. Metoda analogii historycznych - polegająca na przenoszeniu prawidłowości zmian w czasie jednych zjawisk na inne zjawiska, zachodzące w tym samym obiekcie. W tym przypadku ważne jest by użyte zmienne były względem siebie różnoimienne. Innymi słowy by: cykl życia jednych produktów można było przenosić na cykl życia innych produktów. Przykładowo:

• rozwój radiofonii (mierzony liczbą posiadaczy odbiorników) może być podstawą przewidywań rozwoju telewizji.

4. Metoda analogii przestrzenno-czasowych - polegająca na przenoszeniu z jednych obiektów do innych prawidłowości zmian zjawiska w czasie. W tym prognozowaniu najczęściej występują zmienne jednoimienne. Przykładowo:

• Tendencja do wzrostu częstotliwości korzystania z samochodów konkretnego modelu i firmy, istniejąca w danym kraju, prawdopodobnie wystąpi w innym kraju;

• Uchwalona ustawa regulująca jakieś prawa gospodarki w krajach zaawansowanych cywilizacyjnie, wywoła prawdopodobnie podobny skutek w krajach z opóźnieniem rozwoju cywilizacyjnego, itp.

Metody analogii biologicznych i przestrzennych są najczęściej wykorzystywane do wyznaczania prognoz jakościowych. Natomiast metody analogii historycznych i przestrzenno-czasowych są przede wszystkim wykorzystywane do obliczania prognoz ilościowych.

Wraz z kryterium podziału prognoz na ilościowe i jakościowe, w przypadku prognozowania analogowego pojawia się problem metodologiczny polegający na określaniu podobieństwa zmiennych.

W przypadku prognoz ilościowych (na których skupia się wykład), należy stosować ilościowe kryteria ustalania podobieństwa. Są nimi:

• Kryterium podobieństwa poziomu,

• Kryterium podobieństwa kształtu.

Według kryterium podobieństwa poziomu - dwie zmienne są podobne jeżeli w pewnym momencie (lub okresie) osiągnęły jednakową wartość. W prognozowaniu wykorzystuje się tylko taką sytuację, gdy zmienna prognozowana później niż porównywana, osiąga ten sam poziom. Można to zilustrować wzorem analitycznym:

<

gdzie:

- oznacza wartość zmiennej (Y) w obiekcie prognozowanym

w momencie lub okresie (t);

- oznacza wartość zmiennej (Y) w k-tym obiekcie prognozowanym

w momencie lub okresie (t).

Kryterium to może być wykorzystywane tylko w stosunku do zmiennych jednoimiennych.

Według kryterium podobieństwa kształtu - dwie zmienne są podobne jeżeli charakteryzują się podobnymi zmianami w czasie, tj. mają podobne tendencje rozwojowe, wahania sezonowe lub cykliczne. Kryterium to może być stosowane do zmiennych jednoimiennych i różnoimiennych.

Zastosowanie kryterium podobieństwa kształtu oznacza że w prognozowaniu opieramy się na kierunkach zmian w czasie badanych zmiennych. Ograniczając rozważania do tendencji rozwojowych, można powiedzieć że w tendencjach wyraża się dążenie obiektów do osiągania pożądanych stanów zmiennych. Zmienna która nie zasygnalizowała zmian takich jakie występują w innych obiektach nie może uzyskać prognozy przez analogię.

Podsumowanie

Dla zachowania pełnej poprawności procesu prognozowania, istotne znaczenie ma rozróżnienie typów zmiennych, dla których analizuje się powiązania ze zmienną prognozowaną. Wyróżnić tu można dwa zasadnicze przypadki:

1. Prognozowanie zmiennych powiązanych ze zmienną czasową,

2. Prognozowanie zmiennych powiązanych z innymi niż zmienna czasowa zmiennymi.

Podejście pierwsze (1) określić można jako prognozowanie dynamiki, gdyż jako wynik otrzymujemy bezpośrednio wartość zmiennej prognozowanej badanego obiektu w momentach (okresach) należących do przyszłości.

Podejście drugie (2) określa się mianem prognozowania formy związku, z uwagi na to że główne zadanie polega na odgadnięciu przyszłej formy związku między zmiennymi w prognozowanym obiekcie.

Znajomość formy związku pozwala z kolei na wyznaczenie prognozy zmiennej prognozowanej przy założeniu że występują określone wartości zmiennych objaśniających.

By móc efektywnie stosować metody prognozowania przez analogię, zarówno zmiennych powiązanych ze zmienną czasową jak i innymi zmiennymi niż zmienna czasowa, spełnione muszą być dwa podstawowe warunki:

• Prognosta musi dysponować danymi liczbowymi o zmiennej prognozowanej i zmiennych objaśniających w postaci odpowiednio długich szeregów przekrojowo-czasowych;

• Prognosta musi dysponować odpowiednimi miarami, pozwalającymi ustalić stopień podobieństwa obiektów według określonych z góry kryteriów (podobieństwa poziomu czy podobieństwa kształtu).

Prognozowanie metodą analogii pozwala uzyskiwać prognozy średnio i długookresowe.

2. Metoda analogii historycznych

Metoda prognozowania za pomocą analogii historycznych polega na przenoszeniu prawidłowości zmian w czasie jednych zmiennych na inne zmienne, występujące w tym samym obiekcie. W procesie prognozowania stosuje się następujący podział zmiennych:

• Zmienne wiodące (inna nazwa „wyprzedzające”) - charakteryzują się tym, że zmiany ich wartości następują z pewnym wyprzedzeniem czasowym w stosunku do zmian zmiennej prognozowanej;

• Zmienne zbieżne - zmieniają swe wartości w tym samym czasie, w którym występują zmiany zmiennej prognozowanej;

• Zmienne opóźnione (inna nazwa „naśladujące”) - wykazują opóźnienie czasowe zmian w stosunku do zmian zmiennej prognozowanej.

W praktyce wystarczy że dysponuje się informacją o dwóch z trzech wyżej wymienionych kategorii. Ale koniecznie musi wśród nich być zmienna wiodąca. Drugą jest najczęściej zmienna opóźniona.

Zmienne wiodące służą wyznaczeniu prognozy. Zmienne opóźnione zaś są zmiennymi prognozowanymi. Innymi słowy: Znalezienie zmiennej (zmiennych) wiodących umożliwia przeprowadzenie wnioskowania o przyszłości zmiennych opóźnionych.

Warunkiem koniecznym do tego by móc kontynuować prognozy metodą analogii historycznych, jest:

• Istnienie dużego podobieństwa kształtu trendów wszystkich rodzajów zmiennych, oraz

• Uwzględnienie występowania opóźnień.

Stwierdzenie podobieństwa kształtu wykresów graficznych różnych zmiennych, opiera się często na analizie tzw. „składowych systematycznych” szeregu czasowego danych zmiennych. Każda zmienna aby być przydatną w procesie prognozowania musi opierać się na danych ilościowych kształtowania się danego zjawiska w przeszłości. Takie dane uporządkowane chronologicznie tworzą szereg czasowy. W każdym szeregu czasowym obrazującym kształtowanie się jakiegokolwiek zjawiska społecznego (gospodarczego) można wyróżnić dwie składowe:

1. Składową systematyczną, oraz

2. Składową przypadkową.

Składową systematyczną cechuje to, iż jest to zbiór zestawu czynników, które w sposób stały oddziaływają na dane zjawisko. Składają się na nią następujące czynniki:

• Tendencja rozwojowa (trend);

• Stały (przeciętny) poziom zjawiska;

• Wahania cykliczne lub sezonowe.

Składowa przypadkowa - to tzw. „składnik losowy” (wahania przypadkowe).

Tendencja rozwojowa - zwana trendem - jest długookresową skłonnością do jednokierunkowych zmian (wzrostu lub spadku) wartości prognozowanej danego zjawiska. Jest rozpatrywana jako konsekwencja działania stałego zestawu czynników. W przypadku prognozowania popytu pierwotnego, może to być: liczba potencjalnych klientów, stosowana technologia produkcji czy preferencje konsumentów. Trend obrazuje ogólny kierunek rozwoju badanego zjawiska.

Stały (przeciętny) poziom zjawiska - występuje wówczas gdy w szeregu czasowym nie ma tendencji rozwojowej.

Wahania cykliczne - to długookresowe rytmiczne wahania wartości zjawiska wokół tendencji rozwojowej lub stałego (przeciętnego) poziomu tej zmiennej. W zjawiskach gospodarczych są one często pochodną cyklu koniunkturalnego gospodarki.

Wahania sezonowe - są (również jak wahania cykliczne) - wahaniami analizowanego zjawiska wokół tendencji rozwojowej lub stałego poziomu tej zmiennej, ale dodatkowo wyróżnia je to, że mają skłonność do powtarzania się w czasie (mniej więcej w jednakowych odstępach czasu). W ujęciu rocznym wynikają one z oddziaływania na zjawisko pogody (pory roku), bądź istnienia zwyczajów ludowych.

Wahania losowe - są przejawem stochastycznego charakteru procesów społeczno-gospodarczych. Odznaczają się one całkowitą nieregularnością kierunku i siły występowania. Są zatem elementem nieprzewidywalnym w każdym pojedynczym przypadku.

Analiza szeregu czasowego przedstawionego w postaci graficznej, wskazująca na występowanie wymienionych wyżej składowych szeregu wygląda następująco:

Rysunek: „Składowe szeregu czasowego”

y_t

Wahania cykliczne

Wahania sezonowe

Trend

Stały (średni) poziom

Wahania przypadkowe

Czas

Następny rysunek przedstawia szeregi czasowe z różnymi rodzajami składowych:

Rysunek: „Przykłady szeregów czasowych z różnymi rodzajami składowych”

y_t y_t

Stały (średni) poziom Trend

Czas Czas

y_t y_t

Stały (średni) poziom +

+ wahania sezonowe

Trend +

+ wahania sezonowe

Czas Czas

y_t y_t

Stały średni poziom +

+ wahania cykliczne

Trend +

+ wahania cykliczne

Czas Czas

Wielkość opóźnień między zmienną wiodącą a pozostałymi zmiennymi (w szeregach czasowych posiadających wahania cykliczne), jest pomiarem liczby jednostek czasu dzielących okres (moment) występowania maksimum (minimum) wartości zmiennej wiodącej w danym cyklu i okres (moment) występowania maksimum (minimum) wartości zmiennej zbieżnej lub opóźnionej w tym samym cyklu. Można to zapisać następująco:

lub

Oznaczenia:

„p” - oznacza wielkość opóźnienia;

- oznacza numer okresu (momentu) o najwyższej wartości zmiennej wiodącej

- oznacza numer okresu (momentu) o najwyższej wartości

zmiennej opóźnionej (lub zbieżnej);

- oznacza numer okresu (momentu) o najniższej wartości zmiennej wiodącej;

- oznacza numer okresu (momentu) o najniższej wartości

zmiennej opóźnionej.

Jeżeli w szeregach czasowych poszczególnych klas zmiennych udaje się zaobserwować wiele cykli, a opóźnienia między ich wartościami ekstremalnymi w obrębie poszczególnych cykli nie są jednakowe i jedynie nieznacznie wahają się, wówczas dla celów prognostycznych przyjmuje się średnią z opóźnień zaobserwowanych w poszczególnych cyklach.

Proces wyznaczania prognozy wymaga w dalszym etapie pracy - skonstruowania modelu zmiennej prognozowanej. Możemy spotkać trzy rodzaje takich modeli:

(1)

(2)

(3)

gdzie:

- oznacza wartość zmiennej opóźnionej w momencie (okresie) „t”;

- oznacza wartość zmiennej wiodącej w momencie (okresie) „
”

(t = 1, 2, ..., n); (i = 1, 2, ..., m);

W modelach (1) i (2) występuje jedna zmienna objaśniająca, z tym że w pierwszym z nich rozważa się jedno opóźnienie (p). W drugim kilka opóźnień (p₁, p₂, ...., p_m). W modelu (3) występuje więcej niż jedna zmienna objaśniająca, wraz z charakterystycznymi dla każdej z nich poziomami opóźnień.

Przykład budowy modelu prognostycznego, z przypadkiem jednej zmiennej opóźnionej i jednej zmiennej wiodącej:

Przedsiębiorstwo produkuje od dość dawna proszek do prania białej bielizny, prowadząc zarazem rozległą promocję. Proszek ten cieszy się na rynku dużym powodzeniem. Od pewnego momentu przedsiębiorstwo podjęło produkcję płynu do prania bielizny kolorowej, licząc że dzięki utrwaleniu znaku firmowego w świadomości klientów i reklamie płynu, a także małej zmienności otoczenia przedsiębiorstwa, sprzedaż płynu będzie kształtowała się podobnie jak proszku.

Budowa modelu do podanej treści:

Podane przesłanki są wystarczające by zastosować prognozowanie analogowe. Zmienną opóźnioną (sprzedaż płynu) oznaczamy symbolem (Y), natomiast potencjalną zmienną wiodącą (sprzedaż proszku) oznaczamy symbolem (X). Jako wzór analityczny modelu zmiennej prognozowanej posłużymy się wzorem modelu (1).

Horyzont prognozy w przypadku dwóch zmiennych, wyznaczony jest przez ilość jednostek czasu stanowiących opóźnienie. W przypadku zaś większej liczby zmiennych, przez najmniejsze opóźnienie (pi) spośród wszystkich opóźnień poszczególnych zmiennych objaśniających.

Praktyczne wykorzystanie omówionej metody - prognozowania opartego na analogii historycznej - przedstawione jest w postaci rozwiązań do zadań zawartych w materiałach do ćwiczeń z danego wykładu.

4. Metoda analogii przestrzenno-czasowych

Metody analogowe służą do prognozowania polegającego na przewidywaniu przyszłych wartości badanej zmiennej, przy wykorzystaniu informacji dotyczących innych zmiennych, których przebieg (chodzi tu o składowe szeregu: trend, wahania okresowe - /czyli cykliczne i sezonowe/ , wahania losowe - /inna nazwa - przypadkowe/), w czasie poprzedzającym okres na który się prognozuje - był podobny. Dodatkowo owe zmienne objaśniające zachodzą w tym samym obiekcie, ale mają różne miana.

Zmienne które się porównuje ze zmienną prognozowaną, mogą być względem niej:

• zmiennymi przyczynowymi, lub też

• zmiennymi symptomatycznymi.

Metody analogowe umożliwiają budowanie prognoz średnio i długookresowych. Każda prognoza powinna być obliczona wraz z odpowiednim miernikiem dokładności. Jednak w przypadku metod analogowych nie ma możliwości oszacowania „ex ante” błędów prognozy. Ich dopuszczalność określa się jedynie przy użyciu błędów „ex post” dla prognoz wygasłych.

Efektem takiego prognozowania są wyniki przedstawiane jako: prognozy jakościowe lub prognozy ilościowe. Ponieważ dokładniej interesują nas wyniki prognoz podawane jako zmienne ilościowe stąd dokładniej zajmiemy się dwoma spośród wymienionych (na poprzednim wykładzie) czterech metod analogowych. Chodzi tu o: „metodę analogii historycznych”, oraz „metodę analogii przestrzenno-czasowych”.

Analogie biologiczne i przestrzenne wykorzystywane są do wyznaczania jedynie prognoz jakościowych i to ogranicza ich przydatność w naukach ekonomicznych. Natomiast metody historyczne i przestrzenno-czasowe ze względu na ich ilościowy charakter posiadają bardzo istotne znaczenie poznawcze z punktu widzenia nauk ekonomicznych.

W metodzie analogii przestrzenno-czasowych wykorzystuje się znajomość prawidłowości zmian badanego zjawiska w różnych obiektach, w długich przedziałach czasu. Umożliwia to obliczenie prognoz dotyczących przebiegu tego zjawiska w obiekcie, w którym występuje opóźnienie w rozwoju pod tym względem w stosunku do innych rozważanych obiektów. Oznacza to że sytuacja obserwowana obecnie w badanym obiekcie miała już miejsce (z przyjętym poziomem dokładności) w innym obiekcie jakiś czas temu. Im ten okres opóźnienia jest dłuższy tym jest możliwy dłuższy horyzont prognozy.

Przyczyny stosowania analogii przestrzenno-czasowych

W historii rozwoju ludzkości można odnotować bardzo wiele przykładów rozprzestrzeniania się osiągnięć cywilizacyjnych daleko poza obszar, w którym owych osiągnięć dokonano. Przykładowo: odkrycie telefonu, radiofonii, telewizji, czy też wynalezienie i zastosowanie energii jądrowej, itp. Owe tendencje są skutkiem dążenia ludzkości do jak najlepszego zaspokajania swoich potrzeb. Stanowią zarazem bodziec do powstawania nowych potrzeb. Ważne w tym jest spostrzeżenie że stopień zaspokojenia potrzeb ludzkich jest ściśle związany z zamożnością społeczeństwa, i tym większy im jest ono zamożniejsze. Prowadzi to do powstawania tendencji imitacyjnych w społeczeństwach uboższych, które dążą do posiadania tego samego co już posiadają kraje wyżej rozwinięte.

Postawienie tezy że konsumpcja dóbr i usług będzie upodabniać się w poszczególnych krajach - stanowi dobrą przesłankę do stosowania metod prognozowania konsumpcji w krajach słabiej rozwiniętych, poprzez analogię do krajów dominujących. Jeżeli ponadto uwzględnimy fakt, że w ślad za zmianami upodobań popytu - podążają zmiany w produkcji (wielkości, strukturze, kosztach działalności, itp.) to okaże się modele analogii przestrzenno-czasowych mają bardzo szerokie spektrum zastosowań w procesie wnioskowania o przyszłości poszczególnych państw, obszarów, regionów, przedsiębiorstw i innych obiektów.

Są one także przydatne do prognozowania zjawisk demograficznych, gdyż u podstaw wielu zachowań demograficznych tkwią tendencje imitacyjne.

Bardzo ważnym obszarem zastosowań metod analogii przestrzenno-czasowych są międzynarodowe badania porównawcze. Nas interesują głównie analizy dotyczące sytuacji społeczno-ekonomicznej Polski na tle innych krajów, w tym zwłaszcza krajów Unii Europejskiej. W związku ze zmianami jakie zaszły w naszym kraju po 1989 roku, także w zakresie definiowania pojęć mikro- i makro-ekonomicznych oraz zbierania danych statystycznych, dysponujemy krótkimi szeregami czasowymi dla zmiennych charakteryzujących gospodarkę Polski. Wcześniejsze informacje z lat poprzedzających rok 1989 bardzo rzadko mogą być wykorzystywane do budowania ekonometrycznych modeli przyczynowo-skutkowych. Gdy chcemy określić ścieżkę rozwoju Polski w następnych latach pod względem wyróżnionych zjawisk ekonomicznych, możemy wykorzystać analogie o przebiegu badanych zjawisk w latach wcześniejszych, np. w krajach UE.

Takie przeniesienie prawidłowości rozwojowych zaobserwowanych w wyróżnionych krajach-wzorcach, na realia występujące w Polsce musi być uzasadnione. Uzasadniając takie postępowanie trzeba wykazać że wybór krajów-wzorców przeprowadzono w sposób budzący zaufanie.

Procedura stosowania prognozowania

na podstawie analogii przestrzenno-czasowych

• Pierwszym etapem procesu prognostycznego jest ustalenie zbioru obiektów z których dane będą mogły być traktowane jako wzorce dla obiektu prognozowanego. Przy wyborze obiektów prognosta powinien kierować się całą swoją wiedzą o świecie i prognozowanym zjawisku i na tej podstawie doszukiwać się najrozmaitszych wspólnych cech obiektów. Mogą nimi być np.: zbliżona kultura, stosunek ludzi do pracy, nawet ukształtowanie terenu, itp. Zbiór wytypowanych w ten sposób obiektów oznaczamy przez „Ω” Zalicza się do niego również obiekt prognozowany.

• Kolejny etap to zgromadzenie informacji o interesującej zmiennej w postaci odpowiednio długich szeregów czasowych pochodzących z wcześniej wytypowanych obiektów. Zmienne poddane zostają analizie z punktu widzenia długości ich szeregów czasowych i do dalszych rozważań bierze się jedynie te dla których istnieją dostatecznie długie szeregi czasowe. Zbiór obiektów ustalony po tym etapie nazywa się „zbiorem obiektów dostępnych”, a oznacza symbolem „Ω₁”. Szeregi czasowe opisujące poszczególne obiekty oznacza się symbolem „S”.

• W następnym etapie przechodzi się do wstępnej analizy podobieństwa szeregów czasowych zmiennych w poszczególnych obiektach w stosunku do obiektu prognozowanego. Bierze się tu pod uwagę wiedzę o istocie podobieństwa poziomu i kształtu szeregów czasowych. Etap ten powinien umożliwić podjęcie następujących decyzji:

• które obiekty należy wyeliminować ze zbioru „Ω₁” ze względu na dużą różnicę ich historii w stosunku do historii obiektu prognozowanego;

• które obiekty powinno się wyeliminować ze zbioru „Ω₁” ze względu na występowanie luk w ich materiale statystycznym;

• czy w dalszym postępowaniu należy zastosować wyłącznie kryterium podobieństwa kształtu czy też równocześnie kryterium podobieństwa poziomu i kształtu.

Gdy ze zbioru „Ω₁” zostaną wyeliminowane obiekty o których mowa w punktach (a i b), wówczas otrzymamy zbiór „Ω₂” - który nosi nazwę - „zbiór obiektów zakwalifikowanych do dalszych analiz”. Elementy tego zbioru (poszczególne obiekty) oznaczamy jako „w_k” , k = 0,1, ....., s, przy czym symbol „0” przypisuje się obiektowi prognozowanemu.

• Zgodnie z decyzją podjętą w poprzednim etapie (odnośnie kryterium podobieństwa zmiennych), należy obecnie zbadać siłę podobieństwa poszczególnych zmiennych ze zmienną prognozowaną:

• W przypadku gdy zapadła decyzja o obliczeniu prognozy wyłącznie na podstawie kryterium podobieństwa kształtu, wówczas wybiera się pewien najpóźniejszy, dostatecznie długi by pozwolił zaobserwować aktualne prawidłowości zmian w czasie, fragment przedziału szeregu czasowego zmiennej obiektu prognozowanego. Wybrany fragment określa się mianem „przedziału pierwotnego” „w₀”. W całej długości pozostałych szeregów czasowych poszukuje się fragmentów o długości równej długości przedziału pierwotnego „w₀”, poprzedzających początkową datę przedziału „w₀” jak najbardziej podobnych do przedziału pierwotnego obiektu prognozowanego, wykorzystując przy tym miarę podobieństwa funkcji.

Zaleca się przy tym by wybierać te fragmenty których początkowa data jest jak najbardziej oddalona od początkowej daty przedziału pierwotnego „w₀”. Pozwala to na zwiększanie horyzontu prognozy.

Dodatkowo należy przyjąć tzw. wartość krytyczną „m∗” wskazującą minimalne dopuszczalne podobieństwo szeregów czasowych porównywanych obiektów. Wszystkie obiekty których chociaż jeden z szeregów je opisujących osiągnie w porównaniu z przedziałem pierwotnym obiektu prognozowanego wartość miary podobieństwa wyższą lub równą „m∗”, uznaje się za obiekty podobne i łącznie z obiektem „w₀” włączamy do „zbioru obiektów podobnych”, oznaczanego jako „Ω₃”. Powinno się dążyć by liczba obiektów podobnych była jak największa gdyż wzmacnia to zasadność prognozowania.

• Jeżeli zdecydowano się (w poprzednim etapie) na łączne stosowanie kryterium podobieństwa poziomu i kształtu, to na początku wybieramy ostatni dostatecznie długi fragment szeregu czasowego obiektu prognozowanego (przedział pierwotny). W szeregach czasowych obiektów „w_k” (k = 1, 2, ....q) poszukuje się takiego momentu (okresu) na osi czasu od którego najpóźniejsza wartość przedziału pierwotnego najmniej się różni. Warunkiem koniecznym jest aby punkt ten znajdował się we wcześniejszej części szeregu czasowego obiektu „w_k” niż data początkowa przedziału pierwotnego. Znaleziony w ten sposób moment (okres) stanowił będzie końcową wartość przedziału podobieństwa danego obiektu do obiektu prognozowanego „w₀”. Długości fragmentów kończących się w znalezionym punkcie muszą być identyczne z długością przedziału pierwotnego. Dalsza analiza polega na badaniu podobieństwa ustalonych w ten sposób przedziałów dla każdej pary obiektów „w₀” i „w_k”. Procedura badania jest tutaj analogiczna jak przedstawiona w punkcie (a).

• Gdy wszystkie poprzednie etapy analizy zakończą się pozytywnymi wynikami to można przystąpić do konstrukcji tzw. „prognoz cząstkowych”. Konstrukcja prognoz cząstkowych jest jedynie elementem pomocniczym, gdyż celem postępowania jest wyznaczenie prognozy globalnej obiektu „w₀”. By uzyskać te prognozy w pierwszej kolejności dokonuje się przesunięcia szeregów czasowych zmiennych objaśniających wzdłuż osi czasu, tak by pokryły się one z szeregiem czasowym obiektu prognozowanego. Przesunięcie to zostanie osiągnięte gdy ostatnim wartościom każdego z przedziałów przyporządkujemy liczbę „0”. Liczby (-1), (-2), ..., (-j) obserwacjom poprzednim, a liczby 1,2, ...i obserwacjom następnym. Ogólny zapis tej procedury przedstawia tabela:

Tabela: „Przesunięcie przedziałów pierwotnych wzdłuż osi czasu”

Symbol obserwacji	Przyjęty numer obserwacji „t”
	..... (-2) (-!) 0 1 2 .....
Yt^(0)	..... Y(-2)^(0) Y(-1)^(0) Y0^(0) Y1^(0) Y2^(0) …..
Yt^(k)	..... Y(-2)^(k) Y(-1)^(k) Y0^(k) Y1^(k) Y2^(k) …..

Prognozę cząstkową dla obiektu prognozowanego na podstawie informacji z obiektu „w_k” wyznacza się z formuły:

(t = 1, 2, ...., n^(k))

Oznaczenia:

	-	Prognoza zmiennej „Y” w obiekcie „0” w okresie „t”
	-	Wartość zmiennej „Y” w okresie „t” w obiekcie „k-tym”
	-	Stała przesunięcia
n^(k)	-	Liczba obserwacji występująca po przedziale podobieństwa „k-tego” obiektu nie przekraczająca długości tego przedziału

• Ostatnim etapem całego procesu prognostycznego jest konstrukcja prognozy globalnej. Prognoza globalna stanowi przesunięcie szeregu czasowego obiektu prognozowanego o przeciętne wartości prognoz cząstkowych. Proces ten można zapisać następująco:

(t = 1, 2, ..., min n^(k))

Przy czym:

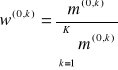
Otrzymana w ten sposób prognoza globalna jest prognozą ostateczną. Maksymalny horyzont wyznaczonej w ten sposób prognozy jest formalnie osiągnięty przez najmniejszą długość przedziału spośród wszystkich rozpatrywanych przedziałów podobieństwa obiektów.

Praca pochodzi z serwisu www.e-sciagi.pl

---