Wykład 9

9. Zasada zachowania pędu

1. Środek masy

Dotychczas przedmioty traktowaliśmy jak punkty materialne, tzn. cząsteczki bezwymiarowe (objętość = 0) obdarzone masą co wystarczało w przypadku ruchu postępowego bo ruch jednego punktu odzwierciedlał ruch całego ciała.

W ogólnym przypadku ruch układu cząsteczek może być bardzo skomplikowany np.

• ciało może wirować lub drgać.

• w trakcie ruchu cząsteczki mogą zmieniać swoje wzajemne położenie
  .

Przykład ciała wirującego jest pokazany na rysunku poniżej.

Zauważmy, że istnieje w tym układzie jeden punkt, który porusza się po linii prostej ze stałą prędkością. Żaden inny punkt nie porusza się w ten sposób. Ten punkt to środek masy. Zajmiemy się ruchem tego punktu.

Zacznijmy od przypomnienia pojęcia średniej ważonej. W tym celu rozważmy prosty układ, w którym mamy do czynienia z dwoma skrzynkami zawierającymi np. jabłka o różnej masie. W jednej mamy n₁ jabłek, każde o masie m₁, w drugiej n₂, każde o masie m₂. Spróbujmy policzyć jaka jest średnia masa jabłka.

czyli

To jest średnia ważona (wagami są ułamki ilości jabłek w skrzynce). Uwzględniamy w ten sposób fakt, że liczby jabłek nie są równe.

Natomiast środek masy jest po prostu średnim położeniem przy czym masa jest czynnikiem ważącym przy tworzeniu średniej.

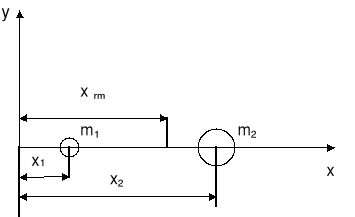
Np. dla dwóch różnych mas m₁ i m₂

czyli

Dla n mas leżących wzdłuż linii prostej otrzymamy

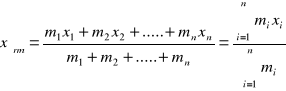
ponieważ suma
jest całkowitą masą układu to możemy zapisać

Gdyby punkty nie leżały na jednej prostej to wówczas środek masy znajdziemy postępując dla każdej ze współrzędnych analogicznie jak powyżej.

Otrzymamy więc

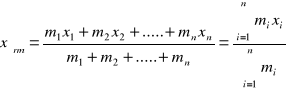
oraz

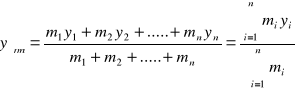
Zwróćmy uwagę, że układ dwóch równań skalarnych można zastąpić przez jedno zwięzłe równanie wektorowe

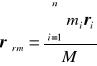
(9.1)

Uogólnienie na trzy wymiary jest automatyczne.

Zauważmy, że środek masy układu punktów materialnych zależy tylko od mas tych punktów i od wzajemnego ich rozmieszczenia (nie zależy od wyboru układu odniesienia).

Przykład 1

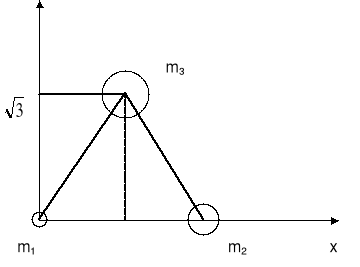
Znaleźć środek masy układu trzech cząstek o masach m₁ = 1kg, m₂ = 2kg i m₃ = 3kg, umieszczonych w rogach równobocznego trójkąta o boku 1m.

Ponieważ wynik nie zależy od wyboru układu odniesienia to możemy przyjąć układ tak jak na rysunku.

x_śrm = (m₁x₁ + m₂x₂ + m₃x₃)/M = (1kg·0m + 2kg·1m + 3kg·0.5m)/6kg = 7/12m

y_śrm = (m₁y₁ + m₂y₂ + m₃y₃)/M = (1kg·0m + 2kg·0m+3kg·m)/6kg = m

Uwaga: położenie środka masy nie pokrywa się z geometrycznym środkiem.

Przedyskutujmy teraz fizyczne znaczenie środka masy.

1. Ruch środka masy

Rozważmy układ punktów materialnych o masach m₁, m₂, m₃ ..., m_n i o stałej całkowitej masie M. Na podstawie równania (9.1) możemy napisać

Mr_śrm = m₁r₁ + m₂r₂ +.......+ m_nr_n

gdzie r_śrm jest środkiem masy w określonym układzie odniesienia. Różniczkując (względem czasu) powyższe równanie otrzymamy

lub

Mv_śrm = m₁v₁ + m₂v₂ +.....+ m_nv_n

Jeżeli ponownie zróżniczkujemy otrzymane powyżej równanie to otrzymamy

lub

Ma_śrm = m₁a₁ + m₂a₂ + .......+ m_na_n

czyli

Ma_śrm = F₁ + F₂ + ...........+ F_n

Wobec tego możemy napisać

Ma_śrm = F_zew (9.2)

Z równania (9.2) wynika, że środek masy układu punktów materialnych porusza się w taki sposób, jakby cała masa układu była skupiona w środku masy i jakby wszystkie siły zewnętrzne nań działały.

To twierdzenie obowiązuje dla każdego układu punktów materialnych.

• Układ może być ciałem sztywnym (punkty mają stałe położenia względem siebie). Wtedy przy obliczeniach środka masy sumowanie zastępujemy całkowaniem.

• Układ może być zbiorem cząsteczek, w którym występują wszystkie rodzaje ruchu wewnętrznego.

Uwaga:

Gdy siłą zewnętrzną jest siła ciężkości to wtedy działa ona na środek ciężkości. W rozważanych przypadkach te dwa środki się pokrywają.

Pojęcie środka masy jest bardzo użyteczne np. do obliczania energii kinetycznej. Obliczmy E_k mierzone w układzie środka masy.

gdzie v_wzgl jest prędkością mierzoną w układzie środka masy. Wykonując mnożenie skalarne otrzymamy

Ponieważ (jak pokazaliśmy wcześniej) wyraz drugi równa się iloczynowi M razy prędkość środka masy (Mv_śrm = m₁v₁ + m₂v₂ +.....+ m_nv_n). W układzie środka masy, w którym mierzymy, v_śrm = 0 więc drugi wyraz znika.

Zatem

gdzie E_k^' jest energią kinetyczną mierzoną w układzie środka masy. Dla ciał sztywnych to równanie przyjmuje postać

gdyż w układzie środka masy ciało sztywne może mieć tylko energię rotacyjną (obrotową).

Przykład 2

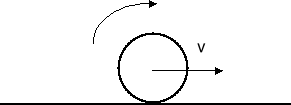
Obręcz o masie m toczy się po płaszczyźnie tak, że środek obręczy ma prędkość v. Jaka jest energia kinetyczna obręczy ?

gdzie v_rot,wzg to prędkość obręczy w układzie środka masy. Ponieważ obserwator w układzie środka masy widzi obręcz obracającą się z prędkością v więc v_rot,wzg = v.

Stąd

Zauważmy, że obręcz ma energię dwa razy większą od ciała o masie m poruszającego się z tą samą prędkością v (ale nie obracającego się).

1. Pęd układu punktów materialnych

Zdefiniowaliśmy już pęd punktu materialnego jako iloczyn jego masy m i prędkości v. Pokazaliśmy również, że II zasada dynamiki Newtona ma postać

Przypuśćmy jednak, że zamiast pojedynczego punktu mamy do czynienia z układem n punktów materialnych o masach m₁, ......, m_n. Zakładamy, że masa układu (M) pozostaje stała. Każdy punkt będzie miał pewną prędkość i pewien pęd. Układ jako całość będzie miał całkowity pęd P w określonym układzie odniesienia będący sumą geometryczną pędów poszczególnych punktów w tym układzie odniesienia

P = p₁ + p₂ + ......... + p_n

Jeżeli porównamy tę zależność z równaniem

Mv_śrm = m₁v₁ + m₂v₂ +.....+ m_nv_n

to otrzymujemy

P = Mv_śrm

Treść tego równania można wyrazić następująco: Całkowity pęd układu punktów materialnych jest równy iloczynowi całkowitej masy układu i prędkości jego środka masy. Ponieważ F_zew = Ma_śrm, to II zasada dynamiki Newtona dla układu punktów materialnych przyjmuje postać

(9.3)

bo

2. Zasada zachowania pędu

Przypuśćmy, że suma sił zewnętrznych działających na układ jest równa zeru. Wtedy na podstawie równania (9.3)

Zasada zachowania pędu: Jeżeli wypadkowa sił zewnętrznych działających na układ jest równa zeru, całkowity wektor pędu układu pozostaje stały.

Zobaczymy jak ta zasada stosuje się do różnych sytuacji fizycznych. Omówimy teraz pojęcie sił zewnętrznych dla danego układu - jak wybrać układ i jak stosować zasadę zachowania pędu.

Przykład 3

Rozważmy dwa ciała o masach m_A i m_B połączone nieważką sprężyną umieszczone na doskonale gładkim stole.
Odciągamy od siebie te ciała na pewną odległość, a następnie puszczamy swobodnie (rysunek). Spróbujmy opisać ruch tych ciał.

Najpierw ustalamy z czego składa się rozważany układ. Przyjmujemy, że tworzą go obie masy + sprężyna. Jeżeli tak to nie działa żadna siła zewnętrzna (działają siły pomiędzy elementami układu czyli siły wewnętrzne). Możemy teraz zastosować zasadę zachowania pędu. Przed zwolnieniem ciał pęd układu (w odniesieniu do stołu) był równy zeru. I taki pozostaje po ich zwolnieniu. Chociaż ciała poruszają się ich pęd może być równy zeru, ponieważ pęd będący wielkością wektorową jest sumą dodatniego pędu ciała A (porusza się w kierunku +x) i ujemnego pędu ciała B (porusza się w kierunku -x). Z zasady zachowania pędu

pęd początkowy = pęd końcowy

0 = m_Av_A + m_Bv_B

Zatem

m_Bv_B = - m_Av_A

lub

v_A = - m_Bv_B/m_A

Np. gdy m_A = 2kg i m_B = 1kg to v_A jest równa połowie v_B i ma zwrot przeciwny.

Przykład 4

Ta sama zasada obowiązuje w fizyce jądrowej i atomowej. Jako przykład rozpatrzmy rozpad promieniotwórczy. Cząstka α (jądro atomu helu) emitowana jest z prędkością 1.4·10⁷ m/s i z energią kinetyczną 4.1 MeV przez jądro uranu 238, pozostające początkowo w spoczynku. Znaleźć prędkość odrzutu powstałego jądra toru 234.

Jako układ rozpatrujemy jądro toru 234 + cząstkę α (przed rozpadem po prostu jądro uranu 238). Ze względu na nieobecność sił zewnętrznych pęd układu, który przed rozpadem był równy zeru po rozpadzie pozostaje niezmieniony.

pęd początkowy = pęd końcowy

0 = M_αv_α + M_Thv_Th

więc

v_Th = - M_αv_α/M_Th = - 4·1.4·10⁷/234 = -2.4·10⁵ m/s

Z. Kąkol-Notatki do Wykładu z Fizyki

9-7

9-7

---