Ćwiczenie 3	Michał Nowak	07.10.2003 r.	Zespół: 1 Grupa: 22
				Wydział Fizyki Tech. i Modelowania Komp.

Badanie Drgań Tłumionych Wahadła Torsyjnego

I. Wstęp teoretyczny:

Bryła sztywna obracalna około stałej osi obrotu i poddana momentowi sił

proporcjonalnemu do kąta odchylenia bryły z położenia równowagi φ, a skierowanemu przeciwnie do wychylenia wykonuje drgania proste, obrotowe o równaniu:

gdzie:

J - moment bezwładności bryły względem osi obrotu.

Rozwiązaniem tego równania jest:

gdzie:

Φ - amplituda kątowa drgań,

ω=
jest częstością kołową drgań,

ε - faza początkowa.

Amplituda i okres są nie zmienne w czasie, przy czym okres nie zależy od amplitudy (izochronizm drgań). Jeżeli oprócz momentu M₁ działają na ciało momenty sił skierowane przeciwnie do prędkości ciała, wówczas amplituda maleje z biegiem czasu; obserwujemy drgania zwane tłumionymi, zanikającymi lub gasnącymi.

Wykres φ(t) dla drgań harmonicznych.

Jeżeli oprócz momentu siły
na ciało działa moment siły zwrócony przeciwnie do jego prędkości kątowej
, to następuje tłumienie ruchu ciała. Przy dużym tłumieniu ruch przestaje być ruchem drgającym.

Przykłady rodzajów tłumienia:

1. kulombowskie (tłumienie tarciem suchym) - tłumienie momentem siły M'=const. zwróconym przeciwnie do prędkości kątowej ciała.

Równanie ruchu ma wtedy postać:

3. wiskotyczne (tłumienie drgań w cieczy lub gazie) spowodowane momentem siły M'' proporcjonalnym do prędkości kątowej i zwróconej do niej przeciwnie:

Równanie ruchu ma wtedy postać:

Wykres φ(t) drgań tłumionych wiskotycznie.

II. Wykonanie ćwiczenia i opracowanie wyników:

zad.1. Badanie drgań obrotowych kuli „nie tłumionych”.

Tabela 1. Pomiar okresu drgań wahadła torsyjnego:

Lp.	1	2	3	4	5	6	7	8	9	10	10
10T[s]	161	162	160	162	161	161	162	160	161	161	161

Średnie odchylenie kwadratowe dane wzorem:

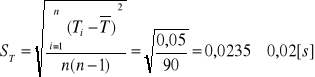
Dla jednego okresu:

S_T= 0,02 [s]

,
dla α=0,99 (trzykrotne odchylenie standardowe)

Zatem okres drgań własnych wahadła torsyjnego wynosi :

T=(16,10 ± 0,06) [s]

Tabela 2. Pomiar amplitudy wychylenia względem czasu dla wahadła nietłumionego:

Lp.	1	2	3	4	5	6	7	8	9	10
xn[dz]l	160	159	159	158	157	157	156	156	156	156

Odległość zwierciadełka od skali: 0,590 ± 0,0005 [m]

Masa kulki: m = 1 [kg]

Promień kulki: R = 0,0313 [m]

Dokładność pomiaru 10T: ± 0,1 [s]

Dokładność pomiaru x_n: ± 0,5 [dz]

Wyliczam moment bezwładności kulki:

Wyliczam moment kierujący k₁:

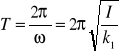
stąd:

T = 16,10± 0,06 [s]

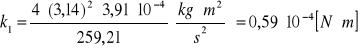
Obliczam niepewność pomiaru k₁ (metoda różniczki zupełnej):

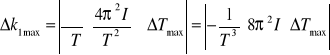
zad.2. Badanie drgań obrotowych kuli tłumionych tarciem kulombowskim.

Tabela 3. Pomiar maksymalnych wychyleń:

Lp.	1	2	3	4	5	6	7
xn[dz]	114	95	70	62	44	26	10

Obliczam moment siły tarcia korzystając ze wzoru:

M_t=
k₁Δϕ ≈

Obliczam niepewność pomiaru M_t (metoda różniczki zupełnej):

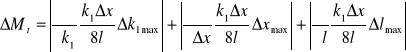
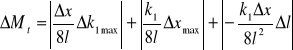
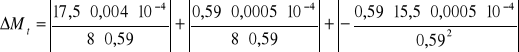
zad.3. Badanie drgań obrotowych kuli tłumionych tarciem wiskotycznym.

Tabela 4. Pomiar okresu drgań tłumionych wahadła torsyjnego tłumionego oporem

wiskotycznym:

Lp.	1	2	3	4	5	6	7	8	9	10	10
10T[s]	164	165	164	165	163	164	165	165	165	162	164

Tabela 5. Pomiar maksymalnych wychyleń:

Lp.	1	2	3	4	5	6	7	8	9	10
xn[dz]	114	104	96	90	83	76	70	65	59	54
ln(xn/dz)	4,73	4,64	4,56	4,49	4,41	4,33	4,24	4,17	4,07	3,98

Obliczam średnie odchylenie standartowe dla pomiaru10T:

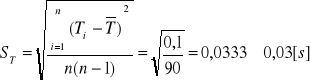
Dla jednego okresu:

S_t =0,03[s]

,
, dla α=0,99 (trzykrotne odchylenie standardowe)

Zatem okres drgań wahadła torsyjnego dla tłumienia wiskotycznego wynosi :

T=(16,40 ± 0,09) [s]

Stosunek tłumienia - stosunek dwóch kolejnych maksymalnych wychyleń po tej samej stronie położenia równowagi.

Logarytmiczny dekrement tłumienia - logarytm naturalny dwóch kolejnych maksymalnych wychyleń (stosunku tłumienia).

Wyliczam współczynnik k₂:

Korzystam ze wzoru ma logarytmiczny dekrement tłumienia D.

Obliczam niepewność pomiaru k₁ (metoda różniczki zupełnej):

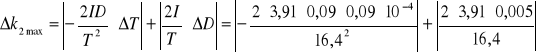
III. Wnioski:

Wszystkie części ćwiczenia zostały wykonane poprawnie o czym świadczą wykresy. Drobne uchybienia mogły być spowodowane niedokładnością ludzkiego oka i przyrządów które mieliśmy do dyspozycji. Jak wynika z obliczeni wszystkie niedokładności mieszczą się w granicach błędów, co nam pozwoliło na powyższe stwierdzenia.

1

T

3T

2T

t

φ

2T

T

3T

t

φ

---