PROJEKT WSTĘPNY

1. WARIANT II

1. Dane ogólne

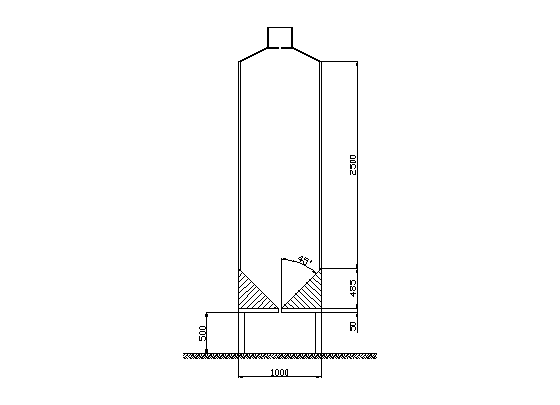
• Średnica wewnętrzna silosu - D = 5,0 m.

• Wysokość komory silosu - H = 25,0 m.

• Grubość ściany komory - h = 0,25 m.

• Wysokość przejazdowa - h_w = 4,50 m

• Objętość całkowita silosu - V = 2072 m³

• Konstrukcja wsporcza - oparcie na 4 słupach żelbetowych

• Przekrycie - stożek żelbetowy ścięty (gr. 0,1 m, nachylenie α = 25°)

• Fundament - żelbetowa płyta kwadratowa

• Lej wysypowy wykonany z chudego betonu (kąt nachylenia leja α = 45°)

1. Geometria silosu

2. Obliczenia statyczne i wymiarowanie

1. Płaszcz silosu

1. Obliczenie naporu materiału sypkiego na ściany silosu

Dane charakterystyczne dla materiału zasypowego (pszenica):

• Ciężar objętościowy - γ = 8,5 kN/m³

• Kąt tarcia wewnętrznego - ϕ = 28°

• Iloraz naporu poziomego i pionowego - λ = 0,53

• Współczynnik tarcia o ścianę silosu - f = 0,35

Dane charakterystyczne dla komory silosu:

• Promień wewnętrzny - r = 5,0 m

• Powierzchnia wewnętrzna komory - A = 78,54 m²

• Obwód wewnętrzny komory - U = 31,41 m

• Promień hydrauliczny - r_h = A/U = 2,5 m

• Rzędna od stożka nasypowego - z_max = 25,9 m

1. Określenie rodzaju przepływu

Rodzaj przepływu określono na podstawie rys. 2 normy PN-89/B-03262. Dla wartości f =0,35 i kąta pochylenia ścian leja α = 40° przepływ ustalono jako rdzeniowy.

2. Napór po napełnieniu komory

• 
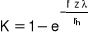
  Napór poziomy materiału sypkiego

- wartość charakterystyczna naporu poziomego

- wartość obliczeniowa naporu poziomego

γ_f = 1,4 - współczynnik obciążenia

• Napór pionowy materiału sypkiego

- wartość charakterystyczna naporu pionowego

- wartość obliczeniowa naporu pionowego

• Napór styczny materiału sypkiego

- wartość charakterystyczna naporu stycznego

- wartość obliczeniowa naporu stycznego

1. Napór poziomy podczas opróżniania

• Równomierny napór poziomy

n₁ = 1,20 - współczynnik wzrostu naporu przy opróżnianiu

p_h0k = n₁⋅p_hnk - wartość charakterystyczna naporu równomiernego

p_h0 = γ _f⋅p_h0k - wartość obliczeniowa naporu równomiernego

• Miejscowy napór poziomy

Napór ten oddziaływuje w dowolnym punkcie ściany komory na powierzchni o wymiarach 0,5r_hx0,5r_h

n₂ = 0,15 - współczynnik wzrostu naporu przy opróżnianiu

p_hlk = n₂⋅p_h0k - wartość charakterystyczna naporu równomiernego

p_hl = γ _f⋅p_hlk - wartość obliczeniowa naporu równomiernego

• Pierścieniowy napór poziomy

Napór ten oddziaływuje w paśmie o szerokości 2r_h powyżej leja ukrytego

H_u = 9⋅f⋅r_h = 7,875 m - wysokość leja ukrytego

p_hrk = 0,2⋅p_h0k - wartość charakterystyczna naporu pierścieniowego

p_hr = γ _f⋅p_hrk - wartość obliczeniowa naporu pierścieniowego

1. Wpływ jednoczesnego napełniania i opróżniania

Wg PN-89/B-03262 uwzględnia się przez zwiększenie wartości równomiernego naporu poziomego p_h0 o 20%.

2. Wpływ pochylenia górnej powierzchni materiału sypkiego.

Należy uwzględnić w silosach, w których r_h>3,0 m. W naszym przypadku r_h = 2,5 m zatem możemy pominąć wpływ nachylenia powierzchni górnej materiału.

3. Wpływ gazowania

Uwzględnia się przez przyjęcie do obliczeń ciśnienia gazu działającego na ściany silosu w tabl. 1 normy. Przyjęto: p_hp = 2,0⋅z kN/m²

4. Zestawienie wyników obliczeń

Wyniki obliczeń parć poziomych po napełnieniu oraz przy opróżnianiu komory zestawiono w tabeli zamieszczonej poniżej.

z	K	phn	ptn	ph0	phl	phr	php
m	-	kN/m^2	kN/m^2	kN/m^2	kN/m^2	kN/m^2	kN/m^2
0,0	0,000	0,000	0,000	0,000	0,000	0,000	0,000
2,0	0,138	11,723	4,103	14,067	2,110	0,000	4,000
3,0	0,200	16,963	5,937	20,356	3,053	0,000	6,000
4,0	0,257	21,829	7,640	26,194	3,929	0,000	8,000
5,0	0,310	26,346	9,221	31,616	4,742	0,000	10,000
6,0	0,359	30,541	10,689	36,649	5,497	0,000	12,000
7,0	0,405	34,435	12,052	41,323	6,198	0,000	14,000
8,0	0,448	38,051	13,318	45,662	6,849	0,000	16,000
10,0	0,524	44,526	15,584	53,432	8,015	0,000	20,000
10,5	0,541	46,000	16,100	55,200	8,280	0,000	21,000
12,0	0,590	50,108	17,538	60,130	9,019	0,000	24,000
12,5	0,604	51,379	17,983	61,655	9,248	0,000	25,000
13,0	0,619	52,603	18,411	63,124	9,469	12,625	26,000
13,5	0,633	53,783	18,824	64,540	9,681	12,908	27,000
14,0	0,646	54,920	19,222	65,904	9,886	13,181	28,000
14,5	0,659	56,016	19,606	67,219	10,083	13,444	29,000
15,0	0,671	57,071	19,975	68,486	10,273	13,697	30,000
15,5	0,683	58,089	20,331	69,706	10,456	13,941	31,000
16,0	0,695	59,069	20,674	70,882	10,632	14,176	32,000
16,5	0,706	60,013	21,005	72,016	10,802	14,403	33,000
17,0	0,717	60,923	21,323	73,108	10,966	14,622	34,000
17,5	0,727	61,800	21,630	74,160	11,124	14,832	35,000
18,0	0,737	62,645	21,926	75,174	11,276	15,035	36,000
18,5	0,747	63,459	22,211	76,151	11,423	0,000	37,000
19,0	0,756	64,244	22,485	77,092	11,564	0,000	38,000
19,5	0,765	65,000	22,750	78,000	11,700	0,000	39,000
20,0	0,773	65,728	23,005	78,874	11,831	0,000	40,000
22,0	0,805	68,386	23,935	82,063	12,309	0,000	44,000
24,0	0,831	70,677	24,737	84,813	12,722	0,000	48,000
25,0	0,844	71,701	25,096	86,042	12,906	0,000	50,000

1. Obliczenie sił wewnętrznych w płaszczu

1. Wartość naporu wiatru na komorę silosu

Wg punktu 2.7.2.2. normy obciążenie konstrukcji wiatrem należy uwzględniać w obliczeniach sił wewnętrznych dla ścian komór okrągłych, dla których r_h>3,0 m. W naszym przypadku wpływ parcia wiatru można pominąć (r_h = 2,5 m).

2. Równoleżnikowe siły rozciągające

N_k = p_h0k⋅r - wartość charakterystyczna

N_k = (p_h0+p_hr)⋅r - wartość charakterystyczna w miejscu działania parcia pierścieniowego

N_o = N_k⋅γ_f - wartość obliczeniowa (γ_f = 1,4)

Zestawienie sił równoleżnikowych

z	ph0	ph0+phr	Nk	No
m	kN/m^2	kN/m^2	kN/m	kN/m
0,0	0,000	0,000	0,000	0,000
2,0	14,067	14,067	70,336	98,470
3,0	20,356	20,356	101,778	142,489
4,0	26,194	26,194	130,972	183,360
5,0	31,616	31,616	158,078	221,309
6,0	36,649	36,649	183,245	256,543
7,0	41,323	41,323	206,613	289,258
8,0	45,662	45,662	228,309	319,633
10,0	53,432	53,432	267,158	374,021
10,5	55,200	55,200	276,002	386,403
12,0	60,130	60,130	300,649	420,909
12,5	61,655	61,655	308,274	431,583
13,0	63,124	75,749	378,745	530,243
13,5	64,540	77,448	387,240	542,136
14,0	65,904	79,085	395,426	553,596
14,5	67,219	80,663	403,314	564,639
15,0	68,486	82,183	410,914	575,280
15,5	69,706	83,648	418,238	585,533
16,0	70,882	85,059	425,295	595,412
16,5	72,016	86,419	432,094	604,932
17,0	73,108	87,729	438,647	614,105
17,5	74,160	88,992	444,960	622,944
18,0	75,174	90,209	451,044	631,461
18,5	76,151	76,151	380,755	533,057
19,0	77,092	77,092	385,462	539,647
19,5	78,000	78,000	389,998	545,997
20,0	78,874	78,874	394,368	552,116
22,0	82,063	82,063	410,315	574,442
24,0	84,813	84,813	424,063	593,689
25,0	86,042	86,042	430,209	602,293

3. Równoleżnikowe momenty zginające

M_αk = ± 0,00006⋅(155-0,375⋅D/h)⋅p_hl⋅D²/4

M_α = M_αk⋅γ_f

4. Momenty zginające wywołane różnicą temperatur

Wpływ temperatury uwzględnia się na podstawie punktu 2.7.2.3. normy.

Przyjęto obliczeniową temperaturę zewnętrzną t_e = -18°C oraz temperaturę wewnętrzną

t_i = +20°C.

R_i = 0,12 m²K/W - opór przejmowania ciepła powietrza wewnątrz

R_e = 0,04 m²K/W - opór przejmowania ciepła powietrza na zewnątrz

R₁ = h/λ₁ = 0,147 m²K/W - opór przejmowania ciepła płaszcza silosu

k = 1/(R_i+R₁+R_e) = 3,257 W/(m²K) - wsp. przenikania ciepła płaszcza

Obliczenie temperatury na zewnętrznej i wewnętrznej powierzchni płaszcza

ϑ_i = t_i - k⋅(t_i - t_e)⋅R_i = 5,15°C - temperatura na powierzchni wewnętrznej

ϑ_e = t_i - k⋅(t_i - t_e)⋅R₁ = - 13,04°C - temperatura na powierzchni zewnętrznej

Δt = ϑ_i - ϑ_e = 18,19°C - gradient temperatur

I_s = 1⋅h³/12 = 1,3⋅10^-3 m⁴ - moment bezwładności przekroju ściany

E_s = 30,5⋅10³ MPa - moduł sprężystości materiału ściany (beton B30)

α_t = 0,00001 1/°C -współczynnik rozszerzalności termicznej ściany

Obliczenie momentów

M_tk = (α_t⋅Δt⋅ E_s⋅ I_s)/h = 29,293 kNm/m - wartość charakterystyczna momentu

M._t = γ _f⋅M_tk = 32,222 kNm/m - wartość obliczeniowa γ_f = 1,1

5. Całkowite momenty zginające

M._ck = M_αk + M_tk - wartość charakterystyczna

M._c = M_α + M_t -wartość obliczeniowa

Zestawienie wszystkich momentów zamieszczono na następnej stronie.

Zestawienie momentów zginających w płaszczu

z	phl	Mk	Mtk	Mck=Mk+Mtk	M	Mt	Mc=Ma+Mt
m	kNm/m^2	kNm/m	kNm/m	kNm/m	kNm/m	kNm/m	kNm/m
0,0	0,000	0,000	29,293	29,293	0,000	32,222	32,222
2,0	2,110	0,443	29,293	29,736	0,620	32,222	32,843
3,0	3,053	0,641	29,293	29,934	0,898	32,222	33,120
4,0	3,929	0,825	29,293	30,118	1,155	32,222	33,377
5,0	4,742	0,996	29,293	30,289	1,394	32,222	33,617
6,0	5,497	1,154	29,293	30,447	1,616	32,222	33,839
7,0	6,198	1,302	29,293	30,595	1,822	32,222	34,045
8,0	6,849	1,438	29,293	30,731	2,014	32,222	34,236
10,0	8,015	1,683	29,293	30,976	2,356	32,222	34,579
10,5	8,280	1,739	29,293	31,032	2,434	32,222	34,657
12,0	9,019	1,894	29,293	31,187	2,652	32,222	34,874
12,5	9,248	1,942	29,293	31,235	2,719	32,222	34,941
13,0	9,469	1,988	29,293	31,281	2,784	32,222	35,006
13,5	9,681	2,033	29,293	31,326	2,846	32,222	35,069
14,0	9,886	2,076	29,293	31,369	2,906	32,222	35,129
14,5	10,083	2,117	29,293	31,410	2,964	32,222	35,187
15,0	10,273	2,157	29,293	31,450	3,020	32,222	35,243
15,5	10,456	2,196	29,293	31,489	3,074	32,222	35,296
16,0	10,632	2,233	29,293	31,526	3,126	32,222	35,348
16,5	10,802	2,268	29,293	31,561	3,176	32,222	35,398
17,0	10,966	2,303	29,293	31,596	3,224	32,222	35,446
17,5	11,124	2,336	29,293	31,629	3,270	32,222	35,493
18,0	11,276	2,368	29,293	31,661	3,315	32,222	35,537
18,5	11,423	2,399	29,293	31,692	3,358	32,222	35,581
19,0	11,564	2,428	29,293	31,721	3,400	32,222	35,622
19,5	11,700	2,457	29,293	31,750	3,440	32,222	35,662
20,0	11,831	2,485	29,293	31,778	3,478	32,222	35,701
22,0	12,309	2,585	29,293	31,878	3,619	32,222	35,841
24,0	12,722	2,672	29,293	31,965	3,740	32,222	35,963
25,0	12,906	2,710	29,293	32,003	3,794	32,222	36,017
25,5	12,993	2,729	29,293	32,022	3,820	32,222	36,042
25,9	13,061	2,743	29,293	32,036	3,840	32,222	36,062

2. Obliczenie mimośrodów i zbrojenia równoleżnikowego (wg PN-B-03264)

Pojawienie się w przekroju ściany silosu momentów zginających powoduje, że przekrój jest rozciągany mimośrodowo. Rozciąganie to może odbywać się na dużym bądź małym mimośrodzie.

Mały mimośród występuje wtedy, gdy w rozpatrywanym przekroju sił znajduje się między zbrojeniem rozciąganym i ściskanym (mniej rozciąganym). W praktyce oznacz to spełnienie warunku: e < 0,5⋅h-a'. Gdy warunek ten nie jest spełniony mamy do czynienia z dużym mimośrodem.

Do obliczeń przyjęto:

a₁ = 0,03 m a₂ = 0,03 m. - otulina zewnętrzna i wewnętrzna

h = 0,25 m - wysokość przekroju

h_o = h - a = 0,22 m -wysokość efektywna przekroju

Beton B-30 f_ck = 30 MPa; f_ctk = 1,8 MPa;

f_cd = 16,7 MPa; f_ctd = 1,20 MPa; E_cm = 30,5⋅10³ MPa

Stal A-III f_yd = 350 MPa; E_s = 200⋅10³ MPa;

• Mimośrody

M_Sd = M._cmax = 36,062 kNm/m. N_Sd = N_omax = 609,509 kN/m

e_e = M_Sd/N_Sd = 0,06 m < 0,5⋅h - a = 0,095 - mały mimośród

e_a = 0,01 m.

e_o = e_e + e_a = 0,07 m

e_s1 = (h/2 - a₁) - e_o = 0,025 m

e_s2 = e_o + (h/2 - a₂) = 0,165 m

• Przekrój zbrojenia

A_s1 = (N_o⋅e_s2)/(f_yd⋅(h_o-a₁) = 15,123⋅10^-4 m²/m - przyjęto φ16 co 130 mm

A_s2 = (N_o⋅e_s1)/(f_yd⋅(h_o-a₂) = 2,291⋅10^-4 m²/m - przyjęto φ16 co 130 mm

Zestawienie obciążeń działających na płytę denną

Ciężar chudego betonu

V_b=1/3*π*r²*h=119,469 m³

G_b=V_b*γ_b=2986,71 kN

G_c=G_b/π*r² + p_v=135,82 kN/m²

G_c^o=140,132 kN/m²

Wymiarowanie konstrukcji wsporczej

• Moment od działania wiatru

I strefa obciążenia wiatrem q_k=0,25 kPa

Budowla jest niepodatna na oddziaływanie dynamiczne β=1,8

Przyjęto do obliczeń teren kategorii A ( otwarty z nielicznymi przeszkodami )

Wysokość budowli

z = 20-40 m

Współczynnik ekspozycji

Wartość współczynnika oporu aerodynamicznego

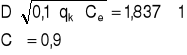
( powierzchnia chropowata )

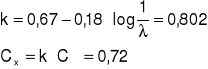
Obciążenie charakterystyczne

Siła ściskająca słup od działania wiatru

• Zestawienie obciążeń działających na konstrukcję wsporczą

Ciężar materiału wsypowego

V=2000m³

γ=8,3 kN/m³

G_1o= V γ γ_f =19920 kN

25

Ciężar płaszcza silosu

Ciężar leja

Całkowita siła działająca na pojedynczy słup

N_c=(G_1o+G_2o+G_3o)/4 +N_w=7126,56kN

Wstępne przyjęcie pola przekroju poprzecznego słupa

---