Laboratorium z mechaniki płynów |
||
Katarzyna Łysiak IIIMDZ;gr. 1006, tydz. a; poniedziałek g. 08:15 |
||
data złożenia
|
data przyjęcia |
ocena |
Temat: Doświadczenie Reynoldsa.
Cel ćwiczenia:
Celem ćwiczenia jest porównanie na drodze obserwacji wizualnej przepływu laminarnego i turbulentnego, oraz wyznaczenie krytycznej liczby Reynoldsa dla przepływu w rurze w przekroju kołowym.
Liczba Reynoldsa jest jedną z tzw. Liczb kryterialnych wyrażających podobieństwo ruchu płynów. Wyraża ona stosunek siły bezwładności do siły tarcia wewnętrznego.
Re = ( V ⋅ d ) / υ
υ = μ / ς
Re = ( ς · v · d ) / μ
Opis ćwiczenia:
Do rury w której płynie woda podłączona jest pionowo, dodatkowa rurka o znacznie większym przekroju. W rurce znajduje się zabarwiona ciecz. Regulujemy prędkość przepływu wody, oraz zabarwionej cieczy. Mierzymy czas obrotu wodomierza, obserwując zmiany przepływu.
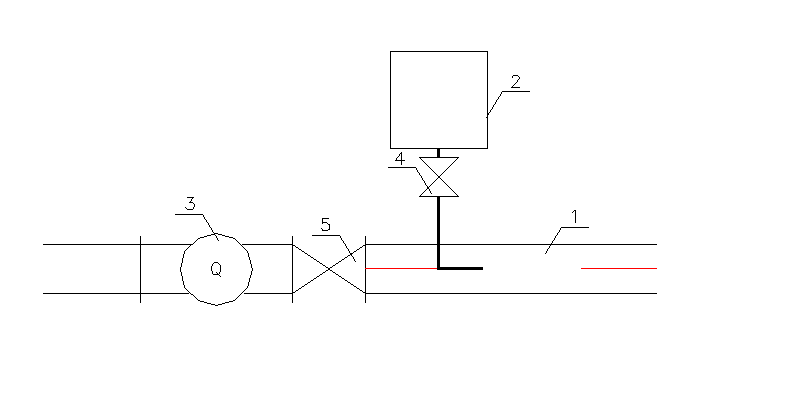
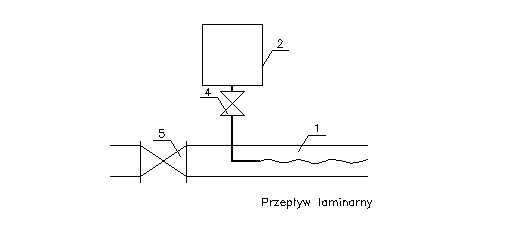
3. Schemat stanowiska.
Stanowisko pomiarowe składa się z rury szklanej 1 o średnicy wewnętrznej D do której doprowadzamy ciecz barwiącą ze zbiorniczka 2, wodomierza 3.

PRZEBIEG ĆWICZENIA
1.Otworzyć zawór 4 doprowadzający barwnik
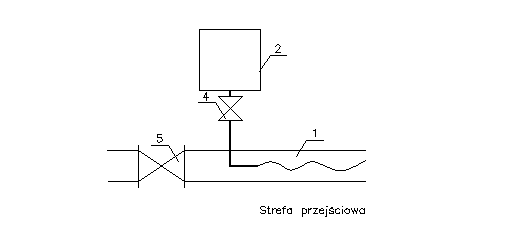
2.Ostrożnie otwierając zawór 5 zwiększać wydatek wody dopływającej do rury. Prędkość przy której rozpocznie się rozpraszanie barwnika po całej objętości płynącego strumienia uważać będziemy za prędkość krytyczną i dla tej wartości wyznaczać będziemy krytyczną liczbę Reynoldsa.
3.Dla prędkości krytycznej należy zmierzyć wartości czasu w których licznik wskazał przepływ 1dm3 wody.
4. Zamknąć zawory.
5. Cykl pomiarowy powtórzyć trzykrotnie.
6. Wyniki pomiarów umieścić w tabelkach pomiarowych.
4. Tabela pomiarowa
Lp. |
I seria pomiarów |
II seria pomiarów |
III seria pomiarów |
|
t[s] |
t[s] |
t[s] |
1 |
45,84 |
31,34 |
11,03 |
2 |
45,75 |
31,37 |
11,13 |
3 |
45,85 |
31,3 |
11,1 |
TH2O = 10o V = 0,001 m3 ρH2O = 1000 kg/m3 d =0,0 315 m2
μ = 1,28*10-6 [m²/s]
Obliczam błędy pomiarowe
t1śr = ![]()
= 29,40
błąd bezwzględny wynosi
t1α I = t1 I - t1 śr = 16,44
t1α II = t1 II - t1 śr = 1,94
t1α III = t1 III - t1 śr = -18,37
średnie arytmetyczne odchylenia pomiarów t1 od wartości średniej
S1α = ± ![]()
![]()
S1α = 24,73
Odczytane z tablic dla trzy krotnego pomiaru
α = 85
t3α = 1,3
Δt1 = ± S1α * t3α = 32,15
t1 = tśr + S1α = 70,54
t2śr = ![]()
= 29,42
błąd bezwzględny wynosi
t2α I = t2 I - t2 śr = 16,33
t2α II = t2 II - t2 śr = 1,95
t2α III = t2 III - t2 śr =-18,29
średnie arytmetyczne odchylenia pomiarów t2 od wartości średniej
S2α = ± ![]()
![]()
S2α = 24,60
Odczytane z tablic dla trzy krotnego pomiaru
α = 85
t3α = 1,3
Δt2 = ± S2α * t3α = 31,98
t2 = tśr + S2α = 55,93
tśr = ![]()
= 29,42
błąd bezwzględny wynosi
t3α I = t3 I - t3śr = 16,43
t3α II = t3 II - t3śr = 1,88
t3α III = t3 III - t3 śr =-18,32
średnie arytmetyczne odchylenia pomiarów t3 od wartości średniej
S3α = ± ![]()
![]()
S3α = 24,68
Odczytane z tablic dla trzy krotnego pomiaru
α = 85
t3α = 1,3
Δt3 = ± S3α * t3α = 32,08
t3 = tśr + S3α = 35,79
Liczby kryterialne Reynoldsa
Re1 = ( V ⋅ d ) / υ
Re1 = 674,013392
Δ Re1 = ±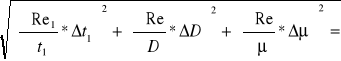
Δ Re1 = ±![]()
Δ Re1 = 10098526,30
Re2 = ( V ⋅ d ) / υ
Re2 = 1399,874
Δ Re2 = ±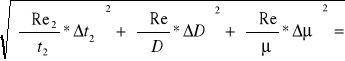
Δ Re2 = ± ![]()
Δ Re2 = 10097677,58
Re3 = ( V ⋅ d ) / υ
Re3 = 2384,970525
Δ Re3 = ±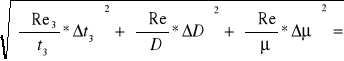
Δ Re3 = ± ![]()
Δ Re3 = 10098135,63
Reśr = ![]()
Reśr = 15891,43
Δ Reśr = ± 10098113,17
5.Tabela obliczeń
Lp. |
Pomiar |
Wartość Re |
tśr |
Średnia wartość |
|
|
|
[s] |
liczby Re |
1 |
I pomiar |
674,013392 |
45,81 |
|
2 |
II pomiar |
1399,874 |
31,34 |
47674,30 |
3 |
III pomiar |
2384,970525 |
11,12 |
|
Wnioski:
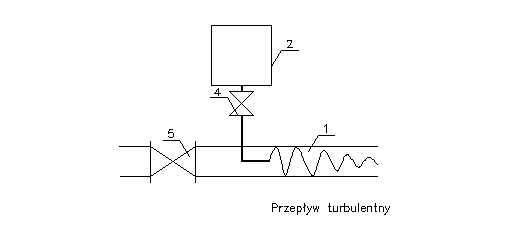
Z przeprowadzonego doświadczenia wynika, że w miarę wzrostu prędkości cieczy w rurze występują składowe prędkości prostopadłe do osi przepływu. Jest to przepływ zwany turbulentnym.
Rysunki przebiegów
1