Nr ćw. 203 |
Data 05.05.01 |
Jakacki Zbigniew |
Wydział Elektryczny |
Semestr II |
Grupa E-3 |
|
Prowadzący: mgr B. Jazurek
|
Przygotowanie |
Wykonanie |
Ocena |
|||
Temat: Wyznaczanie pojemności kondensatora
za pomocą drgań relaksacyjnych.
Kondensatorem nazywamy układ dwóch okładek metalowych dowolnego kształtu rozdzielonych dielektrykiem. W stanie naładowania na każdej z okładek znajduje się ładunek elektryczny Q o przeciwnym znaku, a między okładkami napięcie U. Pojemność kondensatora to stosunek ładunku do napięcia:
![]()
.
Pojemność kondensatora zależy od jego kształtu, rozmiarów, wzajemnej odległości okładek, a także od rodzaju zastosowanego dielektryka.
Pojemność C ładuje się poprzez dołączenie SEM do obwodu zawierającego szeregowo połączone opór R i pojemność C, natomiast rozładowanie przez odłączenie SEM od obwodu.
W dowolnym momencie procesu ładowania na okładkach znajduje się ładunek q, a w obwodzie płynie prąd i. Zgodnie z II prawem Kirchhoffa spadki napięć na kondensatorze i oporniku są kompensowane przez SEM źródła:
![]()
Po zróżniczkowaniu tego równania i uwzględnieniu związku i=dq/dt otrzymamy:
![]()
Jest to równanie różniczkowe o zmiennych rozdzielonych. Po obustronnym scałkowaniu otrzymujemy rozwiązanie:
![]()
gdzie i0 jest stałą całkowania określoną przez warunki początkowe.
W dowolnej chwili napięcie na kondensatorze wynosi Uc=-Ri i zmienia się w czasie zgodnie z równaniem:
![]()
Po dostatecznie długim czasie kondensator zostaje naładowany całkowicie. Praktycznie dla t,
Uc0 kondensator uważa się za naładowany, gdy t=5RC.
Podczas rozładowania prąd i napięcie rozładowywania wynoszą odpowiednio:
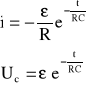
Wielkość RC występującą w powyższych równaniach nazywa się stałą obwodu. Określa ona prędkość ładowania i rozładowywania obwodu.
Jeśli w obwodzie RC dołączymy równolegle do kondensatora neonówkę wówczas występują w obwodzie niesymetryczne wzrosty i spadki napięć na kondensatorze nazywane drganami relaksacyjnymi.
Drgania relaksacyjne polegają na tym, że napięcie na kondensatorze, ładowanym ze źródła, rośnie napięcie aż do pewnej wartości Uz (napięcia zapłonu), kiedy to zapala się neonówka. Neonówka posiada mały opór, więc kondensator szybko się rozładowuje, aż napięcie osiągnie wartość napięcia gasnięcia Ug (neonówka gaśnie). Znów następuje ładowanie kondensatora, jego rozładowanie i tak dalej. Ponieważ opór jarzącej się neonówki jest bardzo mały to czas rozładowania stanowi mały ułamek całego okresu i możemy przyjąć, że okres drgań relaksacyjnych jest rówy czasowi ładowania kondensatora od napięcia Ug do Uz
W pierwszym cyklu ładowania napięcie U0 zostanie osiągnięte po czasie t0, zatem
![]()
gdzie: U0 jest napięciem źródła.
Analogiczne równanie dla chwili t0+T:
![]()
znajdujemy wzór na okres:
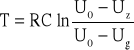
Ostatecznie zastępując logarytm naturalny z powyższego równania (stały dla danej neonówki i danego napięcia) przez K otrzymujemy:
![]()
.
Zatem okres drgań relaksacyjnych jest wprost proporcjonalny do pojemności i oporu.
By obliczyć pojemność kondensatorów najpierw należy wyznaczyć stałą K. W tym celu używamy znanych oporników oraz kondensatora wzorcowego (dekadowego) o znanej pojemności. Okres mierzymy za pomocą sekundomierza (licząc ilość 20 błysków neonówki).
Następnie podłączając do obwodu szukane pojemności możemy obliczyć ich wartości.
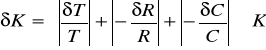
Wyznaczam stałą K oraz błąd δK za pomocą różniczki logarytmicznej:
δR = 15 % wartości rezystora.
a wiec
dla R = 1 MΩ δR = 0,15 MΩ
dla R = 2 MΩ δR = 0,3 MΩ
dla R = 3 MΩ δR = 0,45 MΩ
δT = 0,01 s
δC = 0,01 μF
Wyznaczam stałą K oraz odchylenie standardowe tej wielkości:
L.p. |
Pojemniść C |
Rezystancja R |
Czas t (20⋅ T) |
Okres T |
K |
δK |
|
[F] |
[Ω] |
[s] |
[s] |
|
|
1 |
0,0000002 |
1000000 |
4,97 |
0,248 |
1,242 |
0,262059 |
2 |
|
2000000 |
9,28 |
0,464 |
1,16 |
0,241672 |
3 |
|
3000000 |
13,56 |
0,678 |
1,13 |
0,234252 |
4 |
0,0000004 |
1000000 |
8,69 |
0,434 |
1,086 |
0,215998 |
5 |
|
2000000 |
17,5 |
0,875 |
1,093 |
0,203359 |
6 |
|
3000000 |
26,44 |
1,322 |
1,101 |
0,199144 |
7 |
0,0000006 |
1000000 |
12,79 |
0,639 |
1,065 |
0,19886 |
8 |
|
2000000 |
26,25 |
1,312 |
1,093 |
0,190113 |
9 |
|
3000000 |
40,01 |
2,000 |
1,111 |
0,187255 |
10 |
0,0000008 |
1000000 |
16,31 |
0,815 |
1,019 |
0,190633 |
11 |
|
2000000 |
34,00 |
1,7 |
1,062 |
0,183674 |
12 |
|
3000000 |
51,31 |
2,565 |
1,068 |
0,181509 |
13 |
0,000001 |
1000000 |
20,00 |
1,000 |
1,000 |
0,185439 |
14 |
|
2000000 |
43,53 |
2,126 |
1,063 |
0,17966 |
15 |
|
3000000 |
63,78 |
3,198 |
1,063 |
0,177951 |
Po uśrednieniu otrzymałem wynik:
K = 1,148 ±0,2021
Obliczam pojemności poszczególnych condensatorów (Cx1, Cx2, Cx3), oraz błąd pomiaru za pomocą różniczki logarytmicznej.
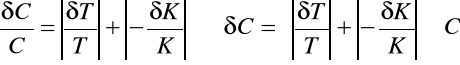
|
Rezystancja R |
Czas t (20 ⋅ T) |
Okres T |
Pojemniść C |
Błąd δC |
|
|
[Ω] |
[s] |
[s] |
[F] |
[F] |
[F] |
1 |
1000000 |
21,78 |
1,089 |
1,187E-06 |
1,535E-07 |
1,503E-07 |
2 |
2000000 |
44,44 |
2,222 |
1,211E-06 |
1,509E-07 |
|
3 |
3000000 |
65,75 |
3,2875 |
1,195E-06 |
1,471E-07 |
|
4 |
4000000 |
89,66 |
4,483 |
1,222E-06 |
1,495E-07 |
|
5 |
5000000 |
113,13 |
5,6565 |
1,234E-06 |
1,503E-07 |
|
1 |
1000000 |
9,59 |
0,4795 |
5,230E-07 |
7,372E-08 |
6,839E-08 |
2 |
2000000 |
18,97 |
0,9485 |
5,173E-07 |
6,758E-08 |
|
3 |
3000000 |
29,56 |
1,478 |
5,374E-07 |
6,817E-08 |
|
4 |
4000000 |
38,72 |
1,936 |
5,279E-07 |
6,613E-08 |
|
5 |
5000000 |
49 |
2,45 |
5,344E-07 |
6,637E-08 |
|
1 |
1000000 |
5,25 |
0,2625 |
2,863E-07 |
4,529E-08 |
3,761E-08 |
2 |
2000000 |
9,72 |
0,486 |
2,650E-07 |
3,728E-08 |
|
3 |
3000000 |
14,47 |
0,7235 |
2,630E-07 |
3,522E-08 |
|
4 |
4000000 |
20,03 |
1,0015 |
2,731E-07 |
3,552E-08 |
|
5 |
5000000 |
24,84 |
1,242 |
2,709E-07 |
3,472E-08 |
|
Po uśrednieniu otrzymałem wyniki:
Cx1 = (1,210 ± 0,153) ⋅ 10 -6 [F]
Cx2 = (5,280 ± 0,683) ⋅ 10 -7 [F]
Cx3 = (2,717 ± 0,376) ⋅ 10 -7 [F]
Wnioski
Otrzymane wartości są zbliżone do rzeczywistych. Choć nie mogę być całkowicie pewien czy nie wystąpił bląd pomiarowy podczas mierzenia stoperem. Co mogło doprowadzić do zniekształcenia ostatecznego wyniku.
Wszystkie obliczenia były dokonywane programem Microsoft Excel
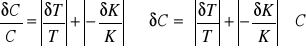
![]()
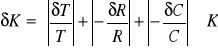
Wyszukiwarka
Podobne podstrony:
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych3, ZiIP Politechnika Poznańska, F
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych6, ZiIP Politechnika Poznańska, F
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych, 203m
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych, 203 , Nr ćw.
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych4
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych5
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych3
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych5
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych3
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych1
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych6
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych2
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych6
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych1
Wyznaczanie pojemności kondensatora za pomocą drgań relaksacyjnych4
WYZNAC~1, ZiIP Politechnika Poznańska, Fizyka II, Ćwiczenia
320, ZiIP Politechnika Poznańska, Fizyka II, Ćwiczenia
310, ZiIP Politechnika Poznańska, Fizyka II, Ćwiczenia
więcej podobnych podstron