Nr 2	Zbigniew Jankowski		PWSZ Kalisz elektroenergetyka	Semestr II	Gr. Ib
Wyznaczenie parametrów ruchu obrotowego były sztywnej		przygotowanie		wykonanie	ocena

1. Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie parametrów ruchu obrotowego bryły sztywnej. Do przeprowadzenia tego ćwiczenie używamy wahadła Oberbecka. Do przymocowanego walca C przymocowane są 4 poziome pręty P, na których umieszczone są walce W, których odległość od środka można regulować. Na górnej części tego urządzenia nawinięta jest nić, która przechodzi przez krążek K, a na końcu nici umieszczony jest ciężarek(walec) o masie m

2. Część teoretyczna

Moment ciężkości odważnika.

Moment bezwładności walca względem jego osi.

Moment bezwładności walca względem średnicy przechodzącej przez środek bryły.

Moment bezwładności pręta względem osi prostopadłej do niego przechodzącej przez jego koniec.

Moment bezwładności

I₀.

Twierdzenie Steinera:

Jeżeli znamy moment bezwładności I_o danego ciała względem pewnej osi przechodzącej przez środek masy tego ciała, to aby obliczyć moment bezwładności I względem dowolnej innej osi, równoległej do niej, należy do momentu bezwładności I_o dodać iloczyn masy ciała i kwadratu odległości d między tymi osiami.

I=I_o+md²

3. Rysunki do ćwiczenia

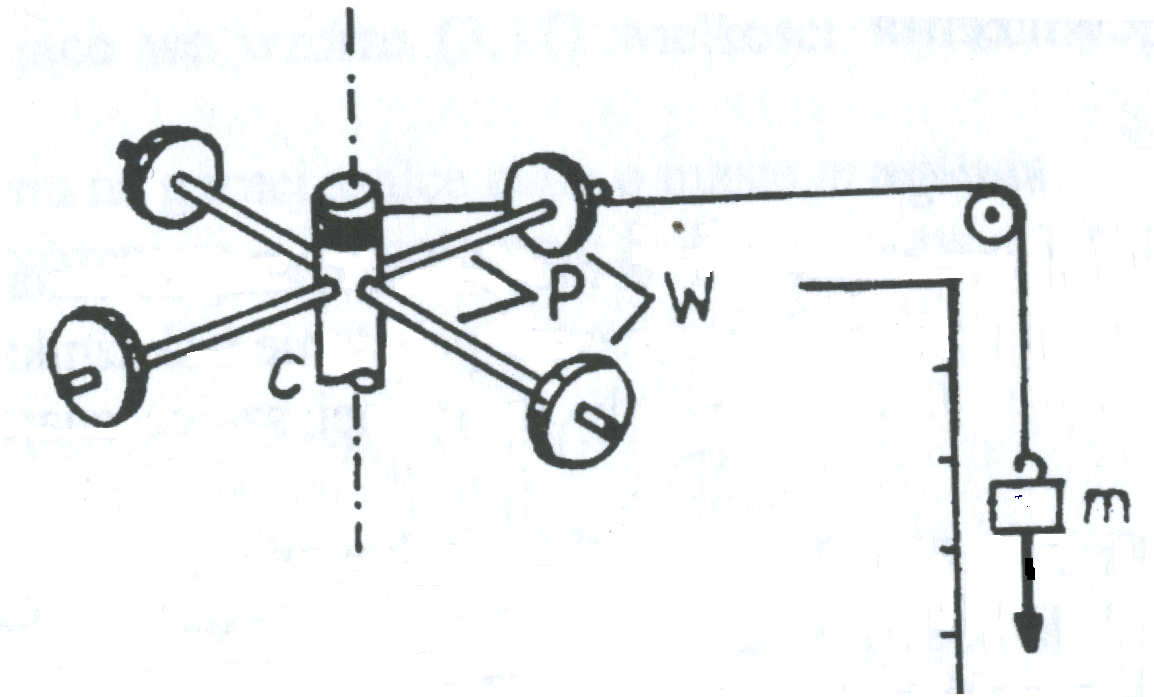
4. Obliczenia

m_w= 0,158kg r_c = 0,01 m.

h_w = 0,014 m d₁ = 0,05m.

l_p = 0,175 m. d₂ = 0,07 m.

r_w = 0,0195 m. d₃ = 0,09 m.

Moment ciężkości działający na bryłę:

M = r × mg = 0,01m × 0,158 kg × 9,81 m/s² × sin 90^o= 0,00158 Nm

Moment bezwładności walca względem jego osi:

I_c = 1/2 Mr_w² =0,5 × 0,00158 Nm × (0,0195m)²= 0.0000003 Nm³

Moment bezwładności krążka:

I_w = M(1/4 r² + 1/12 h²)= 0,00158 Nm[1/4 × (0,0195m)² + 1/12 × 0,014m]

= 0,000001993 Nm³

Moment bezwładności pręta:

I_p = 1/12M×l²=1/12 × 0,00158 Nm × (0,175m)²= 0,000004032 Nm³

Moment bezwładności I_o:

Io = Ic +4Ip+ 4Iw = 0,0000003+4×0,000004032+4×0,000001993=

=0,0000244 Nm³

Całkowity moment bezwładności dla trzech położeń walca:

1. d₁ = 0,05 m.

I₁ = I_o + 4 m_w × d²

I₁ = 0,0000244 + 4 × 0,158 × 0,0025= 0,0016044 Nm³

2. d₂ = 0,07 m.

I₂ = I_o + 4 m_w × d²

I₂ =0,0000244 + 4 × 0,158 × 0,0049 = 0,0031212 Nm³

3. d₃ = 0,09 m.

I₃ = I_o + 4 m_w × d²

I₃ =0,0000244 + 4 × 0,158 × 0,0081= 0,51436 Nm³

d1	0,05m.	t1	10,59 s
d2	0,07 m.	t2	12,60 s
d3	0,09 m.	t3	15,34 s

Stosując regresję liniową, obliczamy współczynnik nachylenia i punktu przecięcia z osią o y.

Wykorzystując powyższą zależność możemy napisać

Σx = (0,05)²+(0,07)²+(0,09)²= 0,0155

Σy = (10,59)²+(12,60)²+(15,34)²=506,2237

Σxy=7,84647

(Σx)²= 0,00024

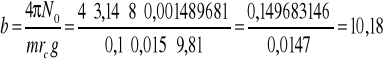
po podstawieniu otrzymujemy:

y=ax+b

Odległość (x)	0,05	0,07	0,09
Czas (y)	10,59	12,60	15,34

5. Błędy pomiarowe mogące występować w ćwiczeniu

W naszym ćwiczeniu mogło występować kilka błędów pomiarowych. Można do nich zaliczyć:

• Błędy związane z niedokładnością suwmiarki (linijki)

• Błędy związane z niedokładnością stopera

• Błędy związane z szybkością reakcji człowieka

Wyliczenia błędów pomiarowych :

∆M = ± 0,001

∆Rc = ± 0,001 [m]

∆Rw = ± 0,001 [m]

∆hw = ± 0,001 [m]

∆l = ± 0,01 [m]

∆d = ± 0,001 [m]

∆mw = ± 0,001 [kg]

∆I_c = │∂I_c/∂M│∆M +│∂I_c/∂R_c│∆R_c = R_c²•∆M /2 + R_c•M•∆R_c = (0,015)²•0,001/2+ + 0,015•0,0147 •0,001 =0,000000112 + 0,00000022=0,000000332

∆I_w = │∂I_w/∂M│∆M + │∂I_w/∂R_w│∆R_w + │∂I_w/∂h_w│∆h_w = (R_w²/4+ h_w²/12)•∆M +

+ (2R_w•M/4+M• h_w²/12)∆R_w + (2h_w•M/12+M• R_w²/4)∆h_w = (0,0198²/4+ 0,015²/12)•0,001 + (2•0,0198•0,0147 /4+0,0147 • 0,0198²/12) •0,001 + (2•0,015•0,0147 /12+0,0147 • 0,0198²/4) •0,001 =0,0001167•0,001+

+(0,0001455+0,00000048) •0,001+(0,0000367+0,00000144) •0,001=

=0,0000003

∆I_p= │∂I_p/∂M│∆M + │∂I_p/∂l│∆l = (l²/12)• ∆M + (2•l•M/12) • ∆l = (0,174²/12)•

• 0,001 + (2•0,174•0,0147/12) • 0,01 = 0,0000018+0,00000426=0,00000606

∆I_o = ∆I_c + 4∆I_p + 4∆I_w = ± 0,000000332+4•0,00000606+4•0,0000003=

=±0,000000332+0,00002424+0,0000012=±0,000025772

∆M = ∂M1/∂I1│∆I1+∂M1/∂α1│∆α1 = α1•∆I1 + I1•∆α1 = 0,174•0,000300706+

+ 0,0173 •0,021= 0,000416

6. Wnioski

Ćwiczenie polegało na zbadaniu parametrów ruchu obrotowego bryły sztywnej.

Po przeprowadzeniu pomiarów zauważełem, że im bliżej osi obrotu ustawiłem walce W, tym mniejszy okazywał się całkowity moment bezwładności I, a tym samym zmniejszał się moment siły M; wzrasta zaś przyspieszenie kątowe.

Im bliżej osi obrotu ustawimy walce W, tym szybciej ciężarek będzie opadał.

---