5. Kinematyka punktu materialnego

Kinematyka jest działem mechaniki zajmującym się ruchem postępowym ciała i jego cechami bez uwzględniania rozmiarów, i masy ciała. Do opisu takiego ruchu wystarczy zbadanie ruchu jednego jego punktu (tzw. „punktu materialnego”, w którym skupiona jest cała masa ciała). Pod pojęciem punktu materialnego rozumiemy ciało o rozmiarach znacznie mniejszych od odległości występujących w danym zagadnieniu. Przykładem takiego punktu materialnego może być zarówno elektron w atomie jak i Ziemia w układzie Słonecznym.

Układy odniesienia

Aby mówić o stanie kinematycznym ciała musimy podać jego położenie w jakimś układzie odniesienia. Położenie to określa tzw. wektor położenia lub wektor wodzący położenia. Najczęściej stosowanymi 3-wymiarowymi układami odniesienia są: układ współrzędnych prostokątnych, układ cylindryczny (lub biegunowy) i sferyczny. Rysunek 14 przedstawia te trzy układy i sposoby przeliczania współrzędnych na współrzędne prostokątne.

Rys 14 Układy współrzędnych: prostokątny, cylindryczny i sferyczny

x = r cosϕ x = r sinθ cosϕ

y = r sinϕ y = r sinθ sinϕ

z = z z = r cosθ

Łatwo sprawdzić, że we wszystkich układach:

x² + y² + z ² = r ².

Ruch ciała to nic innego jak zmiany położenia ciała (wektora wodzącego) w czasie
. Tor ruchu to wykres przestrzenny tej funkcji lub inaczej mówiąc zbiór kolejnych punktów, w których znajduje się ciało z upływem czasu. Ruch ciała możemy podzielić na ruch postępowy i ruch obrotowy bryły.

3.2. Ruch postępowy i obrotowy

Ruch postępowy to taki ruch, w którym nie zmienia się orientacja ciała w przestrzeni (np. ruch postępowy Ziemi wokół Słońca w ciągu roku). Ruch obrotowy to taki ruch, w którym potrafimy wskazać przynajmniej chwilową oś obrotu (oś obrotu to zbiór punktów nieruchomych). Mówimy wtedy także o osiowo symetrycznym polu prędkości punktów ciała materialnego. Przykładem tego ostatniego może być ruch wirowy Ziemi wokół własnej osi.

3.3. Prędkość, pęd, przyspieszenie

Podstawową wielkością kinematyczną opisującą ruch postępowy ciała jest prędkość
będąca pochodną wektora wodzącego
po czasie. Możemy zapisać wzór na prędkość średnią:

,

oraz na prędkość chwilową:

lub we współrzędnych prostokątnych:

,
,
.

W układzie cylindrycznym (3-wymiarowym) lub radialnym (2-wymiarowym) można określić składowe prędkości: radialną
(wzdłuż promienia wodzącego
) i transwersalną
(prostopadłą do promienia wodzącego
).

Uwzględniając zapis wektorowy otrzymujemy:

,
.

Pamiętajmy, że z prędkością związany jest pęd ciała równy iloczynowi masy i prędkości ciała (
).

Wielkością pochodną w stosunku do prędkości jest przyspieszenie
informujące o szybkości zmian wektora prędkości w czasie. W układzie współrzędnych prostokątnych:

oraz

.

We współrzędnych biegunowych otrzymujemy przyspieszenie radialne:

i transwersalne:

.

Ostatni składnik przyspieszenia związany jest z siłą Coriolisa odpowiadającą za podmywanie brzegów rzek płynących z prędkościami posiadającymi niezerowe składowe wzdłuż południka.

Można również przedstawić współrzędne w układzie środka krzywizny toru. Otrzymujemy wtedy składową normalną
(wzdłuż promienia krzywizny R) i styczną
(wzdłuż stycznej do toru).

,
.

Rozkład przyspieszenia na składowe w obu układach obrazuje rysunek 15.

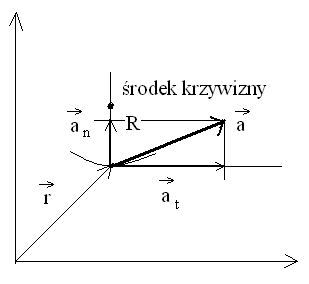
Rys. 15 Rozkład przyspieszenia na składowe biegunowe i w układzie środka krzywizny

Rozpatrzymy teraz przypadek ruchu po okręgu ze stałą prędkością. Ponieważ wartość promienia jest stała dlatego składowa radialna prędkości jest równa zero. Składowa styczna prędkości jest równa:

,

a składowe przyspieszenia:

,

(pamiętając, że
).

Rys. 16 Prędkości i przyspieszenia w ruchu po okręgu

Ostatnią składową przyspieszenia w zapisie wektorowym można przedstawić (sprawdź zgodność kierunków i zwrotów na rysunku 16):

.

Przyspieszenie średnie liczymy podobnie jak prędkość średnią:

.

Mając podane definicje prędkości i przyspieszenia można przeprowadzić podział na różne rodzaje ruchu postępowego (analogicznie - obrotowego). Podział taki dla ruchu postępowego przedstawia rysunek 17.

W postępowym ruchu jednostajnie zmiennym szybkość (prędkość w ruchu prostoliniowym) oraz drogę obliczamy z wzorów:

,

.

Analogiczne wzory stosujemy dla obrotowego ruchu jednostajnie zmiennego.

Rys. 17 Podział ruchu postępowego

3.4. Układy inercjalne i nieinercjalne

Stwierdziliśmy, że aby mówić o ruchu trzeba ustalić układ odniesienia, w którym będziemy opisywać ruch. Wyobraźmy sobie dwa układy odniesienia. Jeden nieruchomy mający początek w punkcie O i drugi poruszający się ruchem postępowym względem pierwszego w kierunku osi OX ze stałą prędkością unoszenia
i mający początek w punkcie O' (rysunek 18).

Rys. 18 Ruch ciała w dwóch układach odniesienia

Wektory wodzące w układzie ruchomym
i w układzie nieruchomym
są ze sobą powiązane wektorem położenia układu ruchomego w układzie nieruchomym
.

Obliczając obustronnie pochodne otrzymujemy względność ruchu na poziomie prędkości ciał:

.

Policzenie kolejnej pochodnej prowadzi do związku między przyspieszeniami:

.

Wyliczając z ostatniego równania
i mnożąc obustronnie przez masę otrzymamy związek między siłami rejestrowanymi w obu układach odniesienia:

,

gdzie siła bezwładności:

.

W obu układach występuje siła rzeczywista
(posiadająca rzeczywiste źródło w postaci konkretnego ciała fizycznego). W układzie ruchomym rejestrowana jest także pozorna siła bezwładności, która nie ma realnego źródła w postaci jakiegoś ciała a pojawia się wskutek rachunkowych przekształceń związku wektorów wodzących (przejścia z jednego układu odniesienia do drugiego). Chcąc doprowadzić do jednakowej postaci równania ruchu w obu układach odniesienia:

należy przyjąć, że siła bezwładności jest równa zero. Warunek ten jest równoważny założeniu, że prędkość unoszenia jest stała. Tak więc możemy powiedzieć, że oba układy są równoważne w opisie ruchu - czyli inercjalne względem siebie gdy nie rejestrujemy w nich sił bezwładności lub inaczej mówiąc gdy poruszają się względem siebie ze stałą prędkością unoszenia (oczywiście także gdy są nieruchome względem siebie).

Z siłami bezwładności mamy do czynienia na każdym kroku (ruszający samochód lub winda, jazda na wirażu, wirówki, karuzele itd.). Wiele nieporozumień budzi pojęcie ciężaru. Dla wyjaśnienia rozważmy stan nieważkości czyli stan braku siły nacisku na podłoże (np. wagę). Ciężar ciała w tym przypadku jest równy zero chociaż działa na niego siła grawitacji. Tak więc na ciężar składają się siła grawitacji i rejestrowane w układzie nieinercjalnym siły bezwładności. Fakt ten (i elipsoidalny kształt Ziemi) powoduje różny ciężar tego samego ciała na różnych szerokościach geograficznych. Na równiku, przeciwna do siły grawitacyjnej, siła odśrodkowa (wynikająca z ruchu wirowego Ziemi) najbardziej wpływa na zmniejszenie mierzonego ciężaru.

5. Ruch w polu grawitacyjnym, rzuty

Na zakończenie tego rozdziału przeanalizujemy ruch ciała w polu grawitacyjnym (rzut ukośny). Jest to doskonały przykład na zastosowanie zasady niezależności ruchów. Mówi ona, że ruch ciała można analizować niezależnie wzdłuż różnych kierunków. Pomijając opory ruchów można powiedzieć, że ciało będzie poruszać się w kierunku poziomym ruchem jednostajnym prostoliniowym natomiast w pionie ruchem jednostajnie zmiennym (rysunek 19).

Rys. 19 Rzut ukośny

Zapisując współrzędne x i y jako funkcje czasu otrzymujemy:

,

.

Wyeliminowanie z nich czasu prowadzi do równania y(x) będącego równaniem paraboli z gałęziami skierowanymi w dół.

.

Z równania tego można wyliczyć zasięg „z” w rzucie ukośnym,

oraz stwierdzić, że maksymalny zasięg uzyskujemy dla kąta  o wartości 45^o (sin2α=1).

---