KINETYKA REAKCJI ENZYMATYCZNYCH

Celem badań kinetyki reakcji enzymatycznych jest uzyskanie informacji o szybkości przemiany substratów w produkty. Ilościowy opis reakcji enzymatycznej przy pomocy modelu kinetycznego może być podstawą do przewidywania szybkości i kierunku danej reakcji w łańcuchu lub cyklu metabolicznym, czyli podstawą określenia katalitycznej sprawności enzymu w organizmie. Nie każda cząsteczka jest zdolna do reakcji jednocząsteczkowej i nie każde zderzenie powoduje zajście reakcji dwu- lub wielocząsteczkowej. Reagują tylko te cząsteczki, które są na odpowiednio wysokim poziomie energetycznym.

W celu przeprowadzenia rozważań na temat kinetyki reakcji enzymatycznych należy określić biologiczne warunki standardowe i podstawowe pojęcia termodynamiki.

Warunki standardowe to:

1. pH = 7

2. Temperatura 25⁰C

3. Wszystkie roztwory są 1 - molowe.

4. Ciśnienie wszystkich gazów ma wartość 1 atmosfery.

Podstawowe pojęcia termodynamiki:

1. Entalpia ( H ) określa zawartość ciepła w organizmie

H = E + pv

gdzie E to energia wewnętrzna, a „pv” to iloczyn ciśnienia i objętości.

2. Entropia ( S ) jest miarą bezładu molekularnego układu. Im większy jest stopień nieuporządkowania, tym większa jest wartość entropii.

3. Energia swobodna (entalpia swobodna nazywana również potencjałem termodynamicznym) ( G ) określa, jaką pracę może wykonać układ.

Wartości bezwzględne entalpii, entropii i energii swobodnej nie są zazwyczaj brane pod uwagę. Rozważane są raczej zmiany tych wartości, co zapisuje się jako ΔH, ΔS, ΔG. Parametry te tworzą następującą zależność:

ΔG = ΔH - TΔS

W warunkach standardowych trzy wyżej wymienione parametry zapisuje się następująco: ΔH⁰ ` , ΔS⁰' , ΔG⁰'

Zmianę energii swobodnej reakcji zachodzącej w warunkach standardowych można wyliczyć odejmując wartość ΔG⁰' substratów do wartości ΔG⁰' produktów lub wprowadzając ją ze stałej równowagi ( K ) dla danej reakcji.

W reakcji

A + B ↔ C+D

ΔG = ΔG⁰' + RT ln

gdzie ΔG jest standardową zmianą energii swobodnej, R jest stałą gazową

( 8,3170 J/1^{o .} mol ), |A| i |B|-molowe stężenia substratów, |C | i |D|-molowe stężenia produktów reakcji. T- oznacza temperaturę w stopniach Kelvina ( ⁰C + 273 ), a ln - logarytm naturalny, który można przekształcić w logarytm dziesiętny mnożąc jego wartość przez 2,303.

ΔG jest miarą spontaniczności reakcji.

Reakcja egzoergiczna - jeśli zmiana energii swobodnej jest mniejsza od zera ( ΔG < 0 ) reakcja może zajść spontanicznie z uwolnieniem energii.

Reakcja endoergiczna - jeśli zmiana energii wewnętrznej jest większa od zera ( ΔG > 0 ) reakcja nie może zajść spontanicznie chyba że zostanie dostarczona energia spoza układu, która umożliwi zapoczątkowanie rekcji.

Reakcje sprzężone - reakcje termodynamicznie niekorzystne mogą być przeprowadzane przez sprzężenie z reakcjami termodynamicznie korzystnymi.

Na przykład synteza glukozo-6-fosforanu ( G-6P ) z glukozy i nieorganicznej grupy fosforanowej jest reakcją endoergiczną . Przy sprzężeniu tej reakcji z hydrolizą ATP do adenozynodifosforanu ADP i nieorganicznej reszty fosforanowej P_i , energia wyzwolona z tej egzoergicznej reakcji, może być wykorzystana w reakcji fosforylacji glukozy.

Glukoza + Pi → G6P + H₂ O; ΔG^o >0

ATP + HOH → ADP + Pi; ΔG^{o 1} <0

sumując powyższe reakcje :

glukoza + ATP → G6P + ADP ; ΔG^o <0

Teoria stanu przejściowego(kompleksu aktywnego opisuje przebieg reakcji jako przejście od substratów(A+B) do produktu (AB) poprzez kompleks aktywny [AB]*

A + B → [AB]* → AB

Kompleks aktywny nie jest jeszcze produktem, ale nie jest także już substratem. Jest stanem nietrwałym, o wysokiej energii. Różnicę między jego energią a energią substratu nazywamy. Energią aktywacji (G_a)

G_a można wyznaczyć z szybkości początkowej (V₀) w różnych temperaturach pod warunkiem przeprowadzenia reakcji w dostatecznie krótkim czasie zapewniając tym jej przebieg z szybkością maksymalną (V_max). Z danych doświadczalnych można sporządzić wykres Arrheniusa, na którym logarytm V₀ odkłada się jako funkcję temperatury bezwzględnej T.

Zależność log V₀ od 1/T jest prostoliniowa. Nachylenie krzywej w stosunku do osi odciętych jest miarą energii aktywacji. Można ją obliczyć ze wzoru :

G_a= 2,3 R

R- stała gazowa 8,317J/1^{o .} mol lub 1,9869 cal/1^{o .}mol

T - temperatura w stopniach Kelwina

Jednak, aby w elementarnej reakcji substraty mogły przejść w produkty muszą być jednocześnie spełnione następujące warunki:

-musi nastąpić kontakt cząsteczki A z cząsteczką B

-cząsteczki A i B muszą posiadać odpowiednią energię, niezbędną do stworzenia

kompleksu aktywnego

-powinna zaistnieć wzajemna orientacja cząsteczek względem siebie tzw. efekt steryczny

Wymogi te spełniają białka enzymatyczne, które są biokatalizatorami reakcji.

Białka enzymatyczne lub inne związki wielkocząsteczkowe mają zdolność tworzenia na swojej powierzchni szczególnego miejsca nazywanego centrum aktywnym enzymu.

Mechanizm działania centrum aktywnego enzymu zależy od jego konformacji (budowy przestrzennej) w obrębie tego centrum. Otoczenie centrum i większość powierzchni enzymu ma charakter hydrofilowy, natomiast samo centrum jest hydrofobowe i posiada jedynie pojedyncze grupy hydrofilowe pełniące funkcje wiązania substratu i biorące udział w procesie katalizy. Obecność tych grup wpływa na sferę elektronów walencyjnych tworzących wiązania odpowiedzialne za przebieg reakcji. Każda katalizowana reakcja jest termodynamicznie możliwa. Rolą katalizatora jest obniżenie energii aktywacji. Odbywa się to dzięki doprowadzeniu substratu do stanu wzbudzenia tj. wytworzeniu nietrwałego związku przejściowego będącego skutkiem przemieszczenia ładunków w obrębie wiązań wodorowych lub podwójnych. W stanie natywnym warunki te spełnia tylko niewielka część cząsteczek substratu (np. rozpad H₂O₂ jest rzędu 10^-11). Niektóre reakcje w warunkach in vitro przebiegają burzliwie z wydzieleniem dużej ilości energii. W organizmach żywych przemiana taka polega na przeprowadzeniu takiej reakcji w sposób kaskadowy tj. rozdzielenie na dwie lub więcej reakcji o niższych wartościach energii aktywacji co umożliwia wykorzystanie jej np. do syntezy ATP przy utrzymaniu stosunkowo niskiej i stałej temperatury przemiany. Enzym dzięki ingerencji w sferę elektronów walencyjnych umożliwia uzyskanie większej ilości unieruchomionych cząsteczek substratu w stanie wzbudzenia.

W badaniach kinetyki reakcji ważną rolę ogrywa ustalenie rzędowości danej przemiany. Rząd reakcji określa ilość atomów lub cząsteczek, których stężenie wpływa na kinetykę reakcji. Zakłada się, że reakcja wg kinetyki I rzędu przebiega tak jakby tylko jeden rodzaj cząsteczek wpływał na mechanizm reakcji. W reakcjach II rzędu taką rolę pełni dwa rodzaje cząsteczek.

Jeśli zapiszemy równanie stechiometryczne reakcji dwuskładnikowej:

_xA + _yB → _zC

to równanie na szybkość reakcji w zależności od stężeń substratów przyjmie postać:

V= K• [A]^x • [B]^y

Rzędowość reakcji wyznacza suma wykładników reakcji w równaniu kinetycznym - czyli x + y.

Jeżeli w badaniach zastosujemy bardzo duży nadmiar substratu „A” to jego stężenie przed i po reakcji będzie praktycznie jednakowe i nie będzie miało wpływu na jej szybkość a stopniowo zwiększamy stężenie substancji „B” to początkowo - reakcja przebiega jako pierwszorzędowa np. reakcje hydrolizy w rozcieńczonych roztworach wodnych. W przypadku, gdy szybkość reakcji jest stała a stężenie substratu nie ma na nią wpływu mówimy o reakcji zerowego rzędu.

Takie warunki istnieją podczas badań aktywności enzymów, gdy reakcja przebiega na granicy faz.

Natomiast, gdy mamy do czynienia z reakcjami przebiegającymi następczo równolegle lub, gdy oba przypadki występują równocześnie po zastosowaniu równań kinetycznych można otrzymać niekoniecznie liczbę całkowitą a o przemianie i jej złożoności można powiedzieć dopiero po wyjaśnieniu mechanizmu danej przemiany.

W odniesieniu do enzymów często mamy do czynienia z reakcją wielocząsteczkową. Jednak dla uproszczenia rozpatrzmy reakcję jednocząsteczkową. Jeśli przyjmiemy, że reakcja enzymatyczna przebiega z utworzeniem kompleksu pośredniego enzym-substrat „ES” i szybko ustala się stan równowagi poprzez rozpad tego kompleksu na enzym i produkt to szybkość początkowa reakcji zależy od stężenia enzymu [E] i początkowego stężania substratu [S]₀. Przy bardzo niskim stężeniu substratu i stałym stężeniu enzymu szybkość reakcji w pewnych granicach jest wprost proporcjonalna do stężenia substratu i przebiega wg kinetyki pierwszego rzędu.

Jeżeli będziemy szukać wyrażenia wiążącego szybkość katalizy ze stężeniem substratu i enzymu oraz szybkościami etapów reakcji to musimy wziąć pod uwagę, że w stanie równowagi szybkość reakcji tworzenia kompleksu jest równa szybkości jego rozpadu na E i S

Jeżeli |E|_p będzie początkowym (całkowitym) stężeniem enzymu, związanego i wolnego a |S| » |E| to do wzoru na stałą równowagi reakcji K₁ ujmującego stężenie wolnego enzymu |E| należy wstawić

|E| = |E|_p - |ES|

stąd |ES| = K₁·|E|· |S|

Szybkość tworzenia kompleksu |ES| V₁=
= K₁ ( |E|_p - |ES|) |S|

Szybkość rozpadu kompleksu |ES| V₂=K₂|ES| + V₃ = K₃ |ES|

-
= K₂|ES| +|K₃|ES|

W stanie równowagi

= -

K₁ ( |E|_p - |ES|) |S| = K₂|ES| + K₃ |ES|

Po przegrupowaniu

=
= K_M

Ta scalona stała nosi miano Stałej Michaelisa- Manten.

Rozwijamy równanie względem |ES|

K_M|ES| =|E|_p |S| - |ES| |S|

K_M|ES| +|ES| |S|=|E|_p |S|

|ES| (K_M+S) = |E|_p |S|

||ES|=

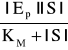
(1)

Ponieważ początkowa szybkość reakcji jest proporcjonalna do stężenia kompleksu |ES|

V=K₃|ES| (2)

Jeżeli |S| »|E|

Następuje pełne wysycenie centrów aktywnych enzymu i wszystkie cząsteczki |E_p| występują w postaci kompleksu |ES|

V=V_max| a |E|= |ES|

V _max= K₃|E| (3)

jeśli |ES| w wyrażeniu (2) zastępujemy wyrażeniem (1)

V = K₃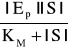

następnie podzielimy przez wyrażenie (3) to otrzymamy

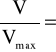
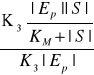
rozwiązując równanie względem V otrzymamy

V=

Jest to równanie Mchaelisa -Manten określające zależność między szybkością reakcji enzymatycznej a stężeniem substratu, jeżeli znane są wartości V_max i K_M. Wykreślanie takich zależności nosi nazwę krzywych wysycenia enzymu substratem. Pełne wysycenie enzymu następuje wtedy, gdy wszystkie centra aktywne enzymu połączą się z substratem. Krzywe takie przybierają kształt hiperboli i dążą asymptotycznie do wartości granicznej „V_max” , którą nazywa się szybkością maksymalną (miano -µmol/min, lub mol/s).

W szczególnym przypadku gdy V=1/2Vmax równanie przyjmie postać

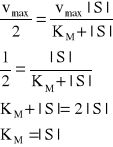
Stężenie substratu, przy którym szybkość reakcji równa jest połowie szybkości maksymalnej nosi nazwę stałej Michaelisa-Manten K_M i dla większości enzymów przyjmuje wartość 10^-5 - 10^-2 mola/dm³ a jej odwrotność jest miarą powinowactwa enzymu do substratu. Wartość ta może ulegać zmianie w zależności od struktury substratu, pH, temperatury i siły jonowej roztworu.

Wykres można przedstawić w postaci liniowej jest to modyfikacja wg Lineweavera-Burka umożliwiająca graficzne wyznaczanie wartości V_max i K_M.

Wyznaczenie zależności 1/V_max od 1/|s| jest opisem kinetyki reakcji enzymatycznej.

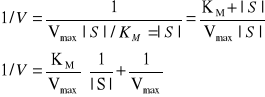
Jeżeli

Jeżeli

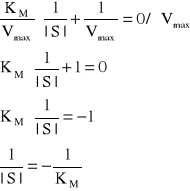
Przecięcie osi rzędnych wyznacza wartość 1/V_max , natomiast punkt przecięcia osi odciętych wyznacza -1/K_M a nachylenie prostej odpowiada K_M/V_max. Wykreślenie krzywej zależności szybkości reakcji przy różnych stężeniach substratu i inhibitora pozwala na określenie rodzaju inhibicji i odróżnienie mechanizmu kompetycyjnego od niekompetycyjnego. Wyznaczenie kinetyki reakcji w obecności inhibitora kompetycyjnego pokazuje, że powoduje on zwiększenie wartości K_M i nie ma wpływu na V_max. Natomiast w obecności inhibitora niekompetycyjnego zmniejszeniu ulega V_max a K_M nie ulega zmianie. Należy zaznaczyć, że reakcja nieodwracalna nie może być charakteryzowana przez tę krzywą.

Szybkość maksymalna V_max wyraża liczbę cząsteczek substratu przekształconych w produkt przez cząsteczkę enzymu w jednostce czasu w warunkach pełnego wysycenia enzymu substratem i liczbowo odpowiada liczbie obrotów, która jest równa stałej kinetycznej K₃ zwanej także stałą katalityczną K_kat. Jeżeli jest znane całkowite stężenie enzymu a właściwie stężeniu miejsc aktywnych |E|_c to szybkość maksymalna V_max równa się liczbie obrotów enzymu

V_max= K₃ |E|_c

K_kat = V_max/|E|_c

K_kat =

W powyższym równaniu w liczniku znajdują się mikromole substratu, a w mianowniku mikromole enzymu. Stała katalityczna K_kat określa liczbowo zdolność enzymu do katalizowania reakcji zwana również reaktywnością.

Podsumowując aktywność enzymu przy danym stężeniu substratu zależy od dwóch cech charakteryzujących enzym: powinowactwa do substratu określanego przez K_M ( wielkość ta dotyczy zdolności wiązania substratu przez enzym) i jego reaktywności wyrażonej przez stałą katalityczną K_kat charakteryzującą rozpad kompleksu aktywnego z uwolnieniem produktu reakcji.

Sposoby wyrażania aktywności enzymów

Miarą aktywności enzymu jest szybkość katalizowanej reakcji. W powszechnym użyciu jest jednostka standardowa enzymu o symbolu J lub (ang.U). Jest to ilość enzymu (lub preparatu enzymatycznego), która katalizuje przemianę 1 µmola substratu w ciągu 1 minuty w optymalnych warunkach reakcji przy stężeniu substratu gwarantującym pełne wysycenie enzymu. Mianem jednostki standardowej jest µmol/min. W praktyce o wyborze metody w tego typu badaniach szybkość reakcji ocenia się na podstawie oznaczenia szybkości przyrostu ilości produktów, ubytku substratów lub zmianą mierzonej wartości fizycznej np. absorbancji w jednostce czasu w zależności od dostępności lub łatwości wykonania oznaczeń i wylicza się ze wzoru

lub

Gdzie: V - szybkość reakcji, ΔP- ilości produktów, ΔS - ilości substratów Δt - czas inkubacji

Stężenie enzymu w roztworze wyraża się liczbą jednostek zawartych w 1 cm³ roztworu (J/cm³).

Stopień czystości preparatów enzymatycznych określa „aktywność właściwa”.

Jest to ilość jednostek standardowych przypadająca na 1 miligram białka (J/mg).

Dla wysoko oczyszczonych enzymów o znanej masie cząsteczkowej podaje się aktywność molekularną.

Jest to liczba moli substratu przekształcanego w produkty w czasie 1min przez 1 mol enzymu w optymalnych warunkach. Wielkość tę można wyrazić liczbą jednostek standardowych na µmol enzymu (J/ µmol) a mianem tej wartości jest 1/min ponieważ (J) wyraża się µmol/min.

Komitet Enzymowy w 1972 roku wprowadził zmiany w definicji jednostki enzymatycznej. Usunięto z definicji określenie „ ta ilość enzymu” ponieważ w badaniu nisko oczyszczonych preparatów enzymatycznych nie da się jej wyrazić w żadnych jednostkach fizycznych. Nowa jednostka nie jest jednoską enzymu (enzyme units) ale jednostką aktywności enzymatycznej (enzymic activity units) (J.a.e.).

Jednostką aktywności enzymatycznej jest ta aktywność, która przekształca 1 mol substratów a czasie jednej sekundy. Jednostkę tę nazwano katalem (kat) i posiada miano mol/s. Można ją wyrazić za pomocą jednostek standardowych.

1 kat= 1mol/s=60 mol/min=
µmol/min=
J.

1 J=µmol/min = 1/60 µmol/s = 1/60 µkat = 16,67
kat

Krzywe progresji

Krzywą progresji określa się szybkość reakcji, która przebiega według zerowego rzędu nosi ona nazwę szybkości początkowej (V₀) i jest podstawą do badania właściwości kinetycznych enzymu. Wykreśla się ją z krzywej zależności szybkości reakcji od czasu trwania reakcji (t₀) przy założeniu:

stężenie enzymu |e|= const.

Początkowe stężenie substratu |S|= const.

(V₀) będzie szybkością początkową jeśli czas trwania reakcji będzie odpowiednio krótki, ponieważ tylko przez krótki czas jest ona prostą. Następnie ulega zagięciu z wielu powodów: zmniejszenie stężenia substratów, hamowanie przez sprzężenie zwrotne, ustalanie stanu równowagi, inaktywacja enzymu.

---