Sprawozdanie z Mechaniki Płynów - laboratorium

Stosunek prędkości średniej do maksymalnej

Pracę wykonali:

Rok II

Grupa IV

Cel ćwiczenia.

Celem ćwiczenia jest doświadczalne wyznaczenie stosunku prędkości średniej do prędkości maksymalnej przepływu płynu w rurociągu, w zależności od liczby Reynoldsa.

Stanowisko pomiarowe.

Schemat stanowiska przedstawia zestaw pomiarowy, który składa się z

wentylatora wywołującego przepływ powietrza przez odcinek rurowy, gazomierza

turbinowego (2) z korektorem objętości (1) oraz z rurki Prandtla (3) połączonej z

mikromanometrem z rurką pochyłą typu MPR-4. Pomiar temperatury powietrza

dokonuje się termometrem.

Ciśnienie atmosferyczne p = 731,3099 [mmHg] = 97500[Pa]

Wilgotność względna powietrza ϕ =67%

Średnica rurociągu D = 52,45 [mm] = 0,05245 [m].

1. Zależności matematyczne

• Natężenie przepływu

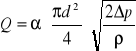
gdzie:

Δp - mierniczy spadek ciśnienia na kryzie

d - średnica kryzy

ρ - gęstość czynnika

α - liczba dobierana z charakterystyki przepływowej kryzy α = 0,623

Gęstość czynnika którym jest powietrze wyznaczymy w oparciu o równanie stanu gazu doskonałego pV = mRT. Wiedząc, że ρ = m/V otrzymamy:

gdzie:

p - ciśnienie atmosferyczne p = 731,3099 [mmHg] = 97500[Pa]

R - stała gazowa dla powietrza R = 287 [m²/s²K]

T - temperatura powietrza T = 24,5 [°C] = 297,5 [K]

Podstawiając dane otrzymamy:

ρ = 1,141 [kg/m³]

Otrzymana gęstość jest gęstością powietrza suchego. Aby uwzględnić wilgoć zawartą w powietrzu należy obliczyć wilgotność bezwzględną X ze wzoru:

gdzie:

ϕ - wilgotność względna ϕ = 67%

p - ciśnienie atmosferyczne [Pa]

p_nas - ciśnienie nasycenia w danej temperaturze (odczytane z tablic)

Znając wilgotność bezwzględną należy odczytać poprawkę gęstości z odpowiedniego wykresu, zależną od wilgoci zawartej w powietrzu suchym. Gęstość powietrza wilgotnego wyznaczymy ze wzoru:

ρ_x = ρ
ε_ρx

gdzie:

ρ_x - gęstość powietrza wilgotnego [kg/m³]

ρ - gęstość powietrza suchego [kg/m³]

ε_ρx - odczytana poprawka ε_ρx = 0,9775

Podstawiając dane otrzymamy:

ρ_x = 1,116 [kg/m³]

• Prędkość maksymalna i średnia:

Prędkość średnią wyznaczamy ze wzoru:

gdzie:

Q - natężenie przepływu

d - średnica otworu kryzy

Prędkość maksymalną wyznaczamy ze wzoru:

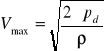
gdzie:

p_d - różnica ciśnień odczytana na manometrze pochyłym

ρ - gęstość powietrza wilgotnego

Stosunek prędkośći średniej do maksymalnej:

• Liczba Reynoldsa

gdzie:

υ - kinematyczny współczynnik lepkości dla powietrza υ = 15,8∙10^-6[m²/s]

d - średnica otworu kryzy

V_śr - prędkość średnia

Tabela z wynikami

Q [m3/s]	Vśr [m/s2]	l [m]	pd	Vmax [m/s2]	Vśr/Vmax	Re	l [m3]
0,03536	15,305345	0,125	990,81	41,64502034	0,367519203	52551,5791	35360000
0,03403	14,729663	0,116	919,47168	40,11779609	0,367160321	50574,9501	34030000
0,03252	14,076069	0,106	840,20688	38,34961468	0,367045911	48330,8074	32520000
0,03133	13,560986	0,098	776,79504	36,8740729	0,367764787	46562,2447	31330000
0,0273	11,816626	0,076	602,41248	32,4724359	0,363897136	40572,9103	27300000
0,02163	9,362404	0,049	388,39752	26,07390699	0,359071773	32146,2289	21630000
0,015778	6,8294041	0,027	214,01496	19,35485643	0,352852221	23449,0615	15778000
0,011361	4,9175345	0,014	110,97072	13,93708953	0,352837981	16884,5727	11361000
0,009389	4,0639672	0,009	71,33832	11,17453157	0,363681216	13953,8115	9389000
0,00533	2,3070556	0,003	23,77944	6,451618809	0,357593296	7921,3777	5330000

Wykres

2. Wnioski.

Z przeprowadzonego ćwiczenia wyznaczyliśmy wartość współczynnika  równego stosunkowi prędkości średniej do prędkości maksymalnej przepływu płynu w rurociągu przy określonych liczbach Reynoldsa. Następnie przedstawiłem na wykresie zależność stosunku prędkości od liczby Reynoldsa. Zauważamy że na przedstawionym wykresie początkowe wartości liczby Reynoldsa tak do 1800 jest bardzo duża rozbieżność Vsr/Vm następnie przy wartości 1800-2500 stosunek Vsr/Vm jest stały zaś powyżej 2500 rośnie wprost proporcjonalnie do liczby Reynoldsa.

1

1

---