3. Rodzaje azymutów. Obliczyć azymuty ciągu sytuacyjnego na podstawie kątów wyrównanych.
Azymut- to kąt zawarty między północną częścią południka odniesienia, a danym kierunkiem poziomym. Wartość azymutu liczy się zgodnie z ruchem wskazówek zegara i wyraża w mierze kątowej, najczęściej w stopniach.
W zależności od przyjętego południka odniesienia wyróżnia się:
azymut geodezyjny.
Azymut magnetyczny- kąt między północną częścią południka magnetycznego a danym kierunkiem poziomym. Jak każdy azymut, liczony jest zgodnie z ruchem wskazówek zegara - od kierunku północy zdefiniowanego przez południk odniesienia, a jego wartość wyrażana jest w mierze kątowej. Azymut magnetyczny może być wyznaczony w terenie z użyciem busoli.
Azymut geograficzny- kąt między północną częścią południka geograficznego a danym kierunkiem poziomym. Jak każdy azymut, liczony jest zgodnie z ruchem wskazówek zegara - od kierunku północy zdefiniowanego przez południk odniesienia, a jego wartość wyrażana jest w mierze kątowej. Azymut geograficzny wyznaczany jest w terenie z użyciem żyroskopu.
Azymut kartograficzny- kąt między północną częścią południka kartograficznego a danym kierunkiem poziomym. Jak każdy azymut, liczony jest zgodnie z ruchem wskazówek zegara - od kierunku północy zdefiniowanego przez południk odniesienia, a jego wartość wyrażana jest w mierze kątowej. Azymut kartograficzny może być wyznaczony kątomierzem na mapie lub obliczony na podstawie różnic współrzędnych.
Azymut topograficzny- kąt między kierunkiem północnym siatki kilometrowej na mapie topograficznej a danym kierunkiem poziomym. Jak każdy azymut, liczony jest zgodnie z ruchem wskazówek zegara począwszy od kierunku północy, a jego wartość wyrażana jest w mierze kątowej.
„DUL
Tyczenie długiej prostej ACB, jeżeli odległości AC i BC nie są znane
Obliczyć wielkości katow na podstawie współrzędnych wierzchołków
Obliczyć dokładność wytyczenia punktu na łuku poziomym mając dane: c=20m +/- 0.01.m,
R=400m, kąt obwodowy = 30 stopni +/-1 minuta” ??????????
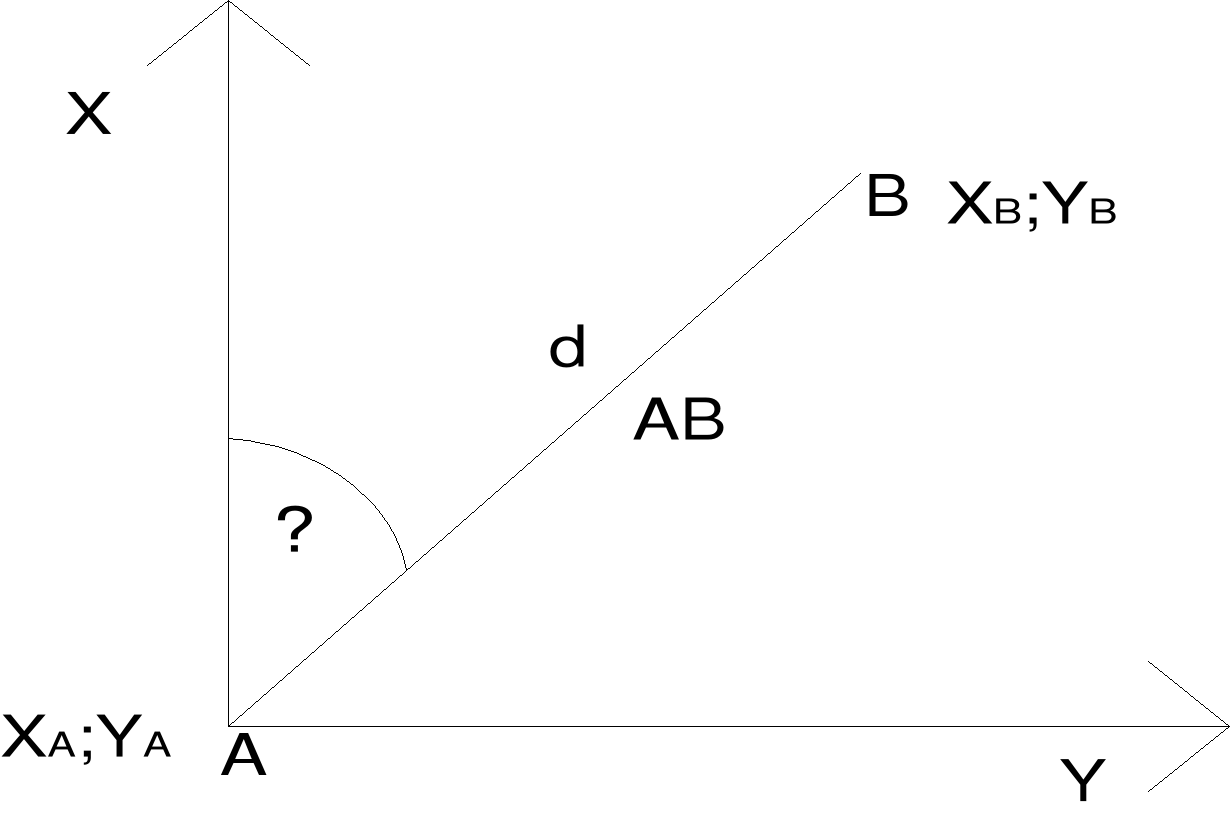
Obliczanie azymutów ciągu sytuacyjnego na podstawie kątów wyrównanych:
![]()
AzAB=αAB
![]()
AzAB=360ْ-αAB
CIĄG OTWARTY:
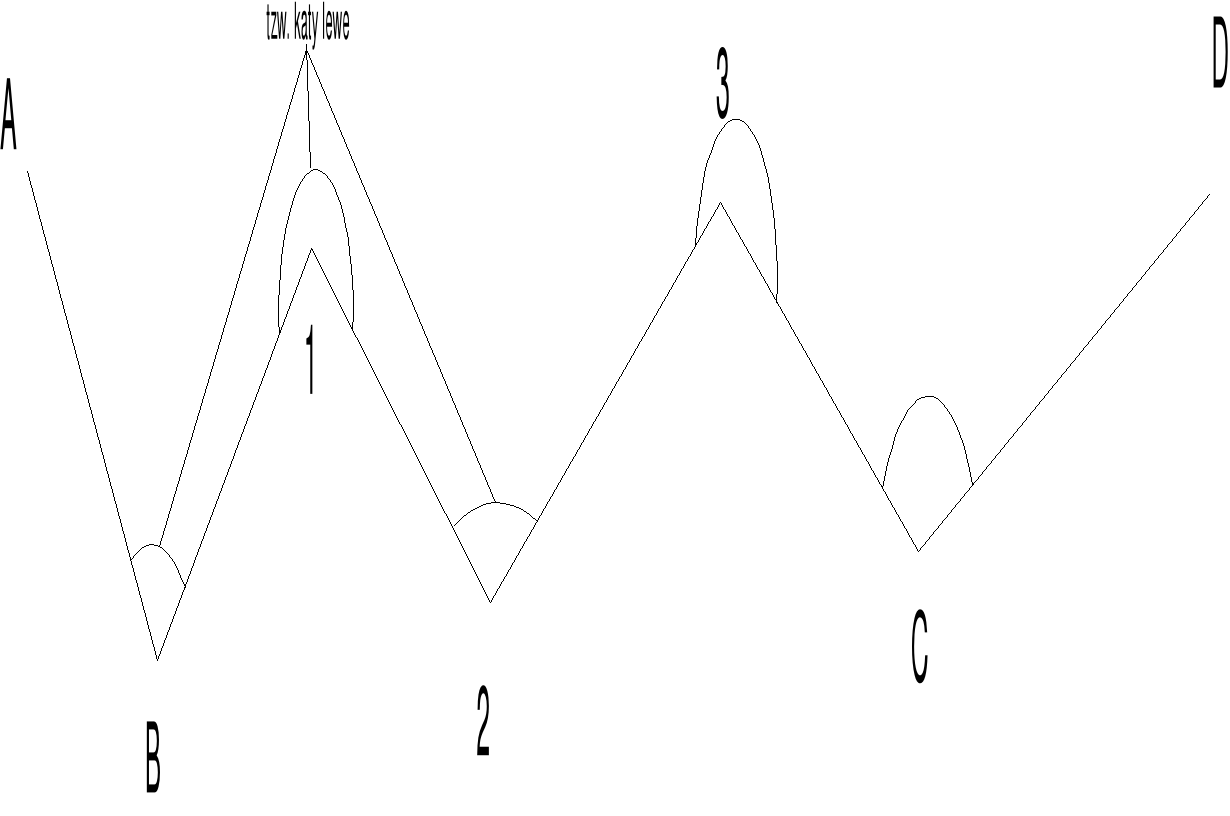
Azn Azn-1 180ْ n Wzór na obliczenie azymutu następnego boku dla kątów lewych
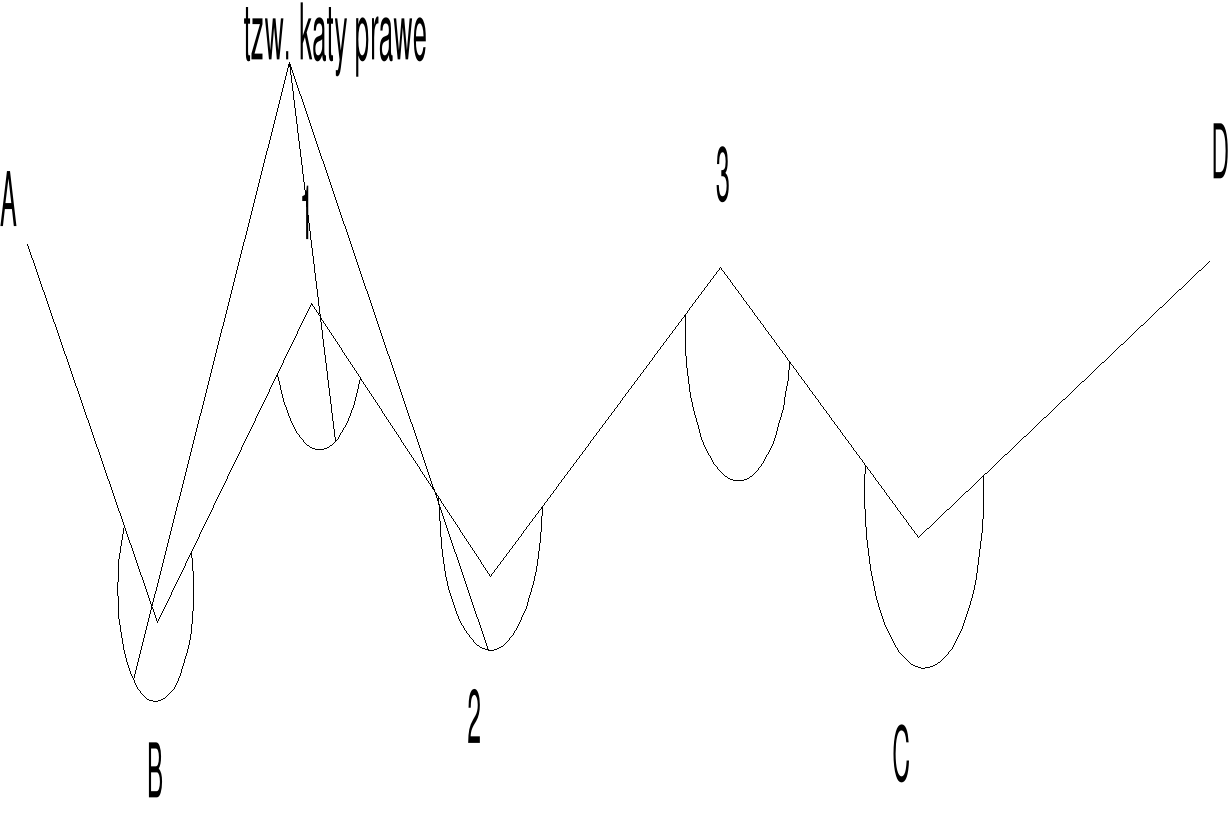
An An1 n 180ْ Wzór na obliczenie azymutu następnego boku dla
kątów prawych
Suma teoretyczna kątów w ciągu otwartym
dla kątów lewych-` ![]()
dla kątów prawych- ![]()
Suma teoretyczna przyrostów w ciągu otwartym
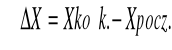
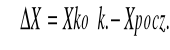
Odchyłka liniowa
![]()
Odchyłki dopuszczalne
Kątowa ![]()
Liniowa ![]()
7. Precyzyjny pomiar odległości metodą modulacji sinusoidalnej (wzory, opis metody, rysunek).
Modulacja- to samorzutna lub celowa zmiana parametrów fali nośnej. Jest to proces fizyczny polegający na oddziaływaniu pewnego przebiegu wielkości fizycznej zwanej sygnałem modulującym na inny przebieg (modulowany) zwany falą nośną , w wyniku czego uzyskuje się przebieg zwany sygnałem zmodulowanym.
Precyzyjny elektroniczny pomiar odległości:
Postać sygnału modulującego w istotny sposób określa
właściwości dalmierzy.
Stosuje się następujące rodzaje modulacji:
1. Modulacja impulsowa używana w dalmierzach laserowych
2. Modulacja sinusoidalna używana w większości pozostałych dalmierzy
3. Modulacja sygnałem pseudo-przypadkowym stosowana w niektórych
dalmierzach hydrograficznych
Do najczęściej stosowanych modulacji należą:
modulacja harmoniczna, w której fala nośna stanowi przebieg sinusoidalny (rys. sinusoidy (wykład lub prezentacja)
modulacja impulsowa, w której fala nośna jest okresowym ciągiem impulsów (rys. wykład lub prezentacja)
Metoda modulacji sinusoidalnej
Sinusoidalny przebieg modulujący falę nośną nadajnika ma zazwyczaj znacznie
mniejszą długość, aniżeli mierzony odcinek L. Najpopularniejsze techniki modulacji sinusoidalnej to:
częstotliwościowa
fazowa
amplitudowa
Proces rozchodzenia się zmodulowanej fali wzdłuż bieżącej drogi x opisuje
równanie fali:
![]()
![]()
,![]()
,![]()
- częstotliwość, pulsacja oraz długość fali wzorcowej;
n - liczba całkowita pełnych kątów 2π zawartych w ,ω, ![]()
,φ,
![]()
- liczba ułamkowa 0<![]()
<1 określająca niepełną część przesunięcia fazowego;
v - prędkość fali pomiarowej
Ze wzoru ![]()
Uzyskuje się kolejne równania:
![]()
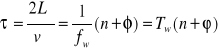
Graniczny błąd pomiaru odległości:
![]()
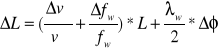
L=1,5km dl=1,15cm
L=15km dl=2,5cm
Rys. prezentacja geodezja.pdf strona 61/95 (nie chciało mi się tego schematu już przerysowywać… Zostawiam miejsce żebyście mogli schemat sobie wrysować
11. Wyznaczenie współrzędnych w obserwacjach GPS z wykorzystaniem pomiaru kodu pseudoodległości.
Odbiornik GPS, aby wyznaczyć pozycję, musi odbierać i śledzić sygnały
satelitarne (by mierzyć pseudoodlegści i przyrosty pseudoodległości) oraz
kolekcjonować depeszę nawigacyjną.
Pseudoodległość jest miarą odległości między satelitą a odbiornikiem w danej
epoce pomiarowej.
Podstawą do jej określenia jest pomiar czasu propagacji sygnału na trasie
satelita - użytkownik na bazie określenia opóźnienia odbieranego przez
odbiornik kodu PRN (pseudoprzypadkowego) w stosunku do jego repliki
generowanej w odbiorniku.
Replika kodu generowana w odbiorniku powinna być synchroniczna
względem kodu generowanego w danym momencie przez satelity systemu.
Ponieważ synchronizacja opiera się na mniej dokładnym zegarze
wewnętrznym odbiornika, jest obarczona pewnym błędem przesunięcia
czasowego.
Błąd ten wpływa bezpośrednio na pomiar opóźnienia propagacyjnego
kodu i nie może być pomijany.
Z tego też powodu pomiar nosi miano pseudoodległości dla odróżnienia od
rzeczywistej odległości geometrycznej, natomiast błąd zegara
użytkownika jest przyjmowany jako jedna z niewiadomych w procesie
określania pozycji.
Każdy odbiornik ma w pamięci wzorce kodów PRN wszystkich satelitów (34kody). Wzorce te są przyrównywane po kolei do odbieranych sygnałów do momentu zidentyfikowania jednego, co oznacza rozpoczęcia śledzenia. Śledzą satelitę odbiornik demoluje depeszę nawigacyjną i odczytuje dane almanachu wszystkich satelitach w konstelacji. Na podstawie danych efemerycznych i almanachu synchronizuje swój zegar wewnętrzny.
Pomiary pseudoodległości są również obarczone błędami wynikającymi z
opóżnień atmosferycznych, niestabilności zegarów satelitarnych i błędnego
modelowania efemeryd satelitów.
Na ogół w formie skalarnej można opisać zależności między
pseudoodległością i rzeczywistą odległością do satelity następującym
wzorem:
Pi = c * (tr - tτ) = di + c * bu + ..pi gdzie:
Pi - pseudoodlegść do satelity i;
tr- czas odebrania sygnału w odbiorniku;
tτ - czas nadania sygnału;
c - prędkość fali elektromagnetycznej w próżni;
di - rzeczywista odległość topocentryczna do satelity;
bu - błąd zegara odbiornika;
pi - łączna wypadkowa błędów wynikających z opóźnień w
jonosferze, troposferze, niedokładności efemeryd, SA itp.
![]()
xi,yi,zi -> znane współrzędne satelitów.
Ri -> pseudoodległość (pomiary)
Jeżeli mamy N>=4 to możemy wyznaczyć 3 współrzędne x,y,z.
Każdy użytkownik systemu GPS, bazując na zmierzonych wartościach
obserwowanych, wcześniej omówionych, oraz wykorzystując odpowiednie
algorytmy nawigacyjne, jest w stanie określić pozycję anteny odbiornika.
Slajd 86/95 plik geodezja.pdf - rysunek.
Wyszukiwarka
Podobne podstrony:
sprawozdanie 02.11.00, Budownictwo UTP, III rok, DUL stare roczniki, drogowe, nawierzchnie adi, obłó
pionowoscobiektu, Budownictwo UTP, III rok, DUL stare roczniki, GEODEZJA, sprawka nasze grupa E, Now
pytania- opracowania, Budownictwo UTP, III rok, DUL stare roczniki, nawierzchnie
TRD-straty czasu na dlugosci linii, Budownictwo UTP, III rok, DUL stare roczniki, trd
pytania egzam tokar, Budownictwo UTP, III rok, DUL stare roczniki, drogowe, Budowa i utrzymanie dróg
nawierzchnie, Budownictwo UTP, III rok, DUL stare roczniki, nawierzchnie
sila sprezajaca, Budownictwo UTP, III rok, DUL stare roczniki, drogowe budowle inżynierskie, przykła
harmonogram1, Budownictwo UTP, III rok, DUL stare roczniki, drogowe, Budowa i utrzymanie dróg
ściaga matka, Budownictwo UTP, III rok, DUL stare roczniki, drogowe, Budowa i utrzymanie dróg
OBCIĄŻENIE TŁUMEM, Budownictwo UTP, III rok, DUL stare roczniki, drogowe budowle inżynierskie, przyk
LINIA ROZDZIAŁU POPRZECZNEGO, Budownictwo UTP, III rok, DUL stare roczniki, drogowe budowle inżynier
k.betonowe-opistechniczny, Budownictwo UTP, III rok, DUL stare roczniki, betony 5 semestr, Projekt 2
Długość rzeczywista drogi startowej, Budownictwo UTP, III rok, DUL stare roczniki, drogowe, Budowa i
gowno adi, Budownictwo UTP, III rok, DUL stare roczniki, drogowe, nawierzchnie adi, obłój ćwiczenia
pomiaryiza, Budownictwo UTP, III rok, DUL stare roczniki, drogowe, Geodezja drogowa, pomiary inżynie
MO strona tytulowa, Budownictwo UTP, III rok, DUL stare roczniki, drogowe budowle inżynierskie, Proj
Obliczenie grubości płyty startowej metodą Westergarda, Budownictwo UTP, III rok, DUL stare roczniki
LINIE WPŁYWU MOMENTÓW ZGINAJĄCYCH, Budownictwo UTP, III rok, DUL stare roczniki, drogowe budowle inż
więcej podobnych podstron