K-03	Komparator
A-2	Forfa Mateusz Mazurek Grzegorz Kilian Tomasz	AGH WEAIiE KANiUP
3 EC
2011/12	Lab. Techniki mikroprocesorowej II

1. Wstęp teoretyczny:

Układy cyfrowe dzieli się na dwie podstawowe grupy:

Układy sekwencyjne

Układy kombinacyjne

W układach kombinacyjnych każda kombinacja sygnałów wejściowych określa jednoznacznie kombinację sygnałów wyjściowych. Z kolei układy sekwencyjne nazywa się układami kombinacyjnymi z pamięcią.

Przykłady bloków kombinacyjnych:

-sumator - cyfrowy układ kombinacyjny, który wykonuje operacje dodawania liczb dwójkowyc

-kubtraktor - układ wykonujący operację odejmowania.

-komparator - układ porównujący dwie liczby dwójkowe.

-transkoder - układ kombinacyjny o n wejściach i k wyjściach, który zmienia dowolny kod cyfrowy (poza kodem 1 z N) na inny, dowolny kod cyfrowy (poza 1 z N). Stosowane przy wyświetlaczach siedmiosegmentowych

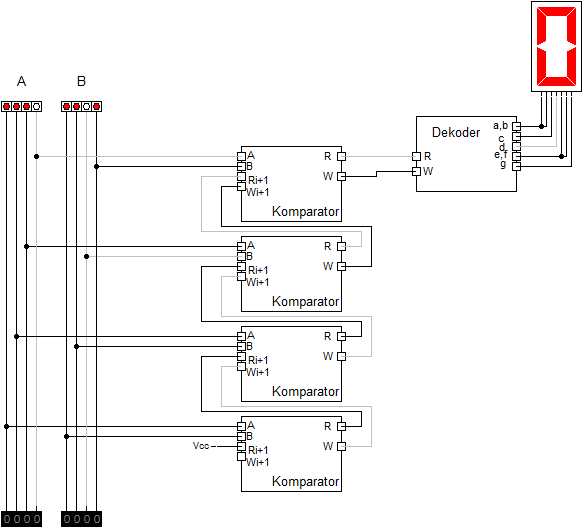
Komparatory można łączyć kaskadowo, co umożliwia porównywanie liczb (w naturalnym kodzie dwójkowym lub w kodzie BCD) o dowolnej długości. Jedynka na jednym z trzech wyjść komparatora informuje, w jakiej relacji względem siebie (mniejsze, równe, większe) są liczby podawane na jego wejścia

2. Realizacja ćwiczenia.

Tabela prawdy komparatora (gdzie x wartość dowolna):

Wejścia					Wyjścia
Ai-1<Bi-1	Ai-1=Bi-1	Ai-1>Bi-1	Ai	Bi	Ai<Bi	Ai=Bi	Ai>Bi
0	0	1	0	0	0	0	1
0	1	0	0	0	0	1	0
1	0	0	0	0	1	0	0
x	x	x	0	1	1	0	0
x	x	x	1	0	0	0	1
0	0	1	1	1	0	0	1
0	1	0	1	1	0	1	0
1	0	0	1	1	1	0	0

gdy Ai=Bi, to wartości wyjść są takie same jak wejść. Jedynkę dla Ai=Bi otrzymamy bramką XNOR. Następnie iloczyn wejścia porównania z poprzedniego komparatora i wyniku bramki XNOR daje nam wyjście

Komparator 1-bitowy:

Znacznie bitów wyjściowych od góry: Ai<Bi; Ai>Bi; Ai=Bi. Na wejście najmłodszego bitu należy zaznaczyć, że wcześniejszy bit był równy. Aby otrzymać komparator wielobitowy wystarczy połączyć wejścia z wyjściami poprzedniego komparatora.

Teraz tworzę tabelę prawdy dla wyświetlacza. Segmenty oznaczone od „a” do „h” według ruchu wskazówek zegara, gdzie „a” jest segmentem górnym, „g” środkowym, a „h” kropką.

Ai<Bi	Ai=Bi	Ai>Bi	a	b	c	d	e	f	g	h
1	0	0	0	0	1	1	1	1	1	0
0	1	0	0	0	0	1	0	0	1	0
0	0	1	1	1	1	0	1	1	1	0

Komparator ma porównać dwie liczby 4-bitowe A i B, a następnie wyświetlić wynik porównania na wyświetlaczu siedmiosegmentowym wg wzoru „A”, gdy liczba A jest większe, „B”, gdy liczba B jest większa oraz „=”, gdy A i B są równe. W tym celu należy zaprojektować transkoder.

Pierwszy krok to zapisanie tablicy prawdy (tabela 3) i tablic Karnaugh'a (tabela 4, tabela 5).

A	B	Ri+1	Wi+1	Ri	Wi
0	0	0	0	0	0
0	0	0	1	0	1
0	0	1	0	1	0
0	0	1	1	1	0
0	1	0	0	0	0
0	1	0	1	0	1
0	1	1	0	0	0
0	1	1	1	0	0
1	0	0	0	0	0
1	0	0	1	0	1
1	0	1	0	0	1
1	0	1	1	0	1
1	1	0	0	0	0
1	1	0	1	0	1
1	1	1	0	1	0
1	1	1	1	1	0

Tabela 3.

Ri+1 Wi+1 Ai Bi	00	01	11	10
00	0	0	1	1
01	0	0	0	0
11	0	0	1	1
10	0	0	0	0

Tabela 4.

Ri+1 Wi+1 Ai Bi	00	01	11	10
00	0	1	0	0
01	0	1	0	0
11	0	1	0	0
10	0	1	1	1

Następnym zadaniem było zaprojektowanie dekodera do wyświetlacza siedmiosegmentowego. W tym celu rozpisaliśmy tablicę dla każdego segmentu. Segment g świeci się w każdym przypadku, a więc wyświetlając „A”, „B” i „=”, zatem w dekoderze połączyliśmy ten segment ze źródłem napięcia.

---