Gdańsk, 05.01.2012r.

Filtry cyfrowe na egzamin zerowy z Przetwarzania Sygnałów 2012

Sylwia Antosik 133442

Ewelina Wielemborek

IBM 3

Spis treści

1. Filtr Swiss Army Knife…………………………………………………………………………………………………………………………………….3

2. Twierdzenia i definicje wykorzystywane w projekcie…………………………………………………………………………………….4

3. Filtr średniej ruchomej…………………………………………………………………………………………………………………………………..5

4. Filtr różnicujący……………………………………………………………………………………………………………………………………………..8

5. Leaky Integrator……………………………………………………………………………………………………………………………………………11

6. Realizacja w Matlabie…………………………………………………………………………………………………………………………………..14

LITERATURA:

• Materiały projektowe „SWISS ARMY KNIFE”

• Treści wykładów “Cyfrowe Przetwarzanie Sygnałów” - prof. dr hab. inż. Ewa Hermanowicz

• Skrypt ” Cyfrowe Przetwarzanie Sygnałów” - dr inż. Andrzej Leśnicki

Swiss Army Knife of Digital Networks

- czyli wielofunkcyjny filtr cyfrowy -

- agregat filtru grzebieniowego FIR (ang. comb filter) i ogniwa bikwadratowego IIR (ang. biquad)

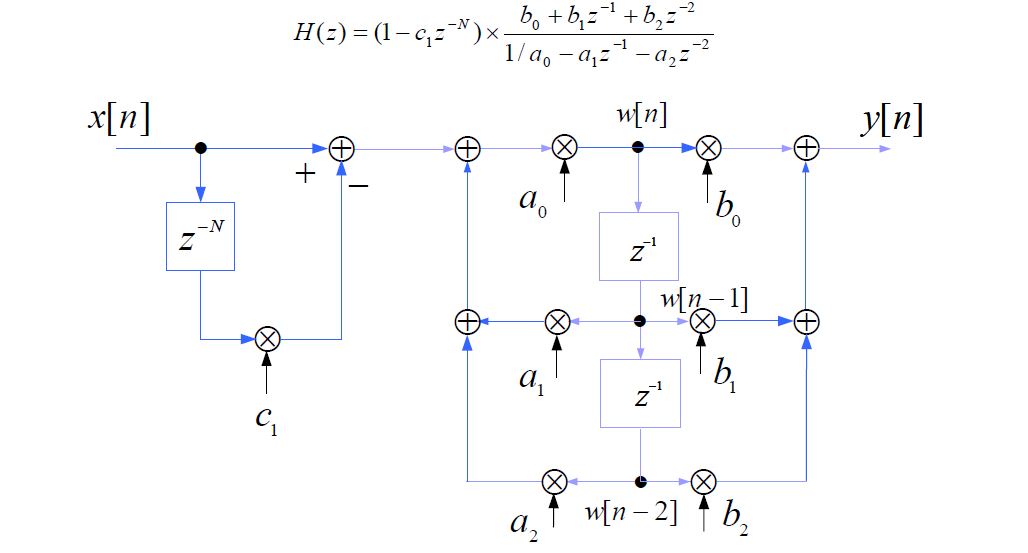
Transmitancja H(z) wielofunkcyjnego filtru cyfrowego

(FC), na podstawie którego można wygenerować filtry pokazane na następnych stronach, o numerach

1., 1.2, 1.1

Twierdzenia i definicje wykorzystywane w projekcie:

Def.1

System odwracalny - System przyczynowy BIBO stabilny o transmitancji H(z) takiej, że

istnieje system odwrotny, czyli przyczynowy BIBO stabilny system o

transmitancji .

Transmitancja systemu odwracalnego ma wszystkie zera i bieguny wewnątrz okręgu jednostkowego.

Def. 2

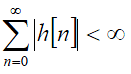
System BIBO  (ang. Bounded Input Bounded Output) stabilny - System przyczynowy z zerowymi warunkami początkowymi o ograniczonej odpowiedzi dla każdego ograniczonego pobudzenia. Warunkiem koniecznym i dostatecznym BIBO stabilności jest

bezwzględna sumowalność odpowiedzi impulsowej

lub położenie biegunów transmitancji wewnątrz okręgu jednostkowego.

Def. 3

System liniowo fazowy - System z uogólnioną liniową charakterystyką fazową
co jest równoważne stałemu opóźnieniu

grupowemu
Jeżeli system liniowo fazowy jest

przyczynowy, BIBO stabilny, ma rzeczywistą odpowiedź impulsową

i wymierną transmitancję, to nie ma innych biegunów niż w zerze,

zera są parami odwrotne i zespolone sprzężone, a odpowiedź

impulsowa h[n] jest skończona. Transmitancja jest wielomianem

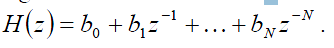
argumentu z^-1 o rzeczywistych współczynnikach

Współczynniki b_i są zarazem próbkami odpowiedzi impulsowej

jednej z czterech typów (z symetrią parzystą lub nieparzystą, z parzystą lub nieparzystą liczbą próbek).

1.Ewelina

Ewelina

Ewelina

2. Filtr różnicujący (ang. Differencer)

Transmitancja układu:

Równanie różnicowe:

y[n]= b₀x[n]-b₁x[n-1]

Charakterystyki wzorcowe filtru:

Opracowane charakterystyki:

Wnioski:

• Filtr nie jest odwracalny, gdyż posiada bieguny i zera na okręgu jednostkowym.

• Zgodnie z definicją trzecią oraz opracowanymi charakterystykami filtru można stwierdzić, że analizowany filtr jest liniowo fazowy. Odpowiedź impulsowa h[n] jest skończona, a rozkład zer i biegunów jest w początku układu współrzędnych.

• W odniesieniu do definicji o BIBO stabilności można wywnioskować, że filtr średniej ruchomej jest BIBO stabilny, dla każdego ograniczonego pobudzenia daje ograniczoną odpowiedź.

3. Filtr średniej ruchomej

(ang. Moving Averager)

Charakterystyki wzorcowe filtru:

Opracowane charakterystyki:

Wnioski:

• Filtr jest odwracalny, gdyż posiada bieguny i zera na okręgu jednostkowym.

• Zgodnie z definicja trzecią oraz opracowanymi charakterystykami filtru można stwierdzić, że analizowany filtr jest liniowo fazowy. Odpowiedź impulsowa h[n] jest skończona, a rozkład zer i biegunów jest w początku układu współrzędnych.

• W odniesieniu do definicji o BIBO stabilności można wywnioskować, że filtr średniej ruchomej jest BIBO stabilny, dla każdego ograniczonego pobudzenia daje ograniczoną odpowiedź.

Przykładowy kod z Matlaba (Moving Averager):

clear all; close all; clc;

%DANE WEJŚĆIOWE

a0 =1;

a1 = 1;

a2 =0;

N=8;

b0=1/N;

b1=0;

b2=0;

c1=1;

%FUNKCJA DOŁĄCZONA DO MATERIAŁÓW PROJEKTOWYCH

fvtool([b0 b1 b2 0 0 0 0 0 -c1*b0 -c1*b1 -c1*b2], [1/a0 -a1 -a2]);

1

14

---