Koncepcja częstotliwości zespolonej. Uogólnienie analizy w stanie ustalonym dla funkcji w postaci wykładniczej
Częstotliwość zespolona i własności
funkcji wykładniczej
![]()
gdzie:
![]()
— amplituda zespolona dla t 0
![]()
— częstotliwość zespolona
Częstotliwość zespolona liczbą rzeczywistą: s σ dla 0
s σ 0
![]()
albo ![]()
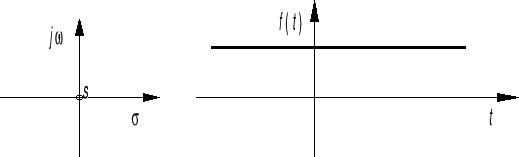
s σ 0
![]()
albo
![]()
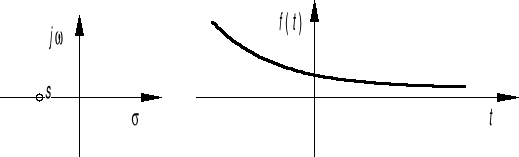
s σ > 0
![]()
albo
![]()
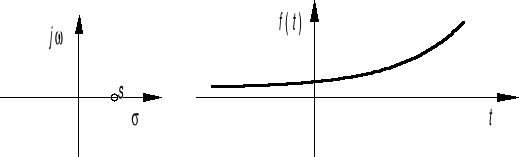
Częstotliwość zespolona liczbą urojoną: s j dla σ 0
s j 0
![]()
albo
![]()
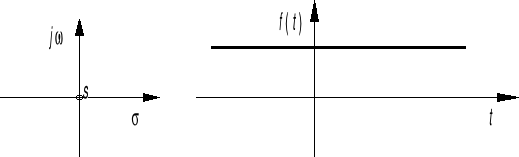
s j
![]()
albo
![]()
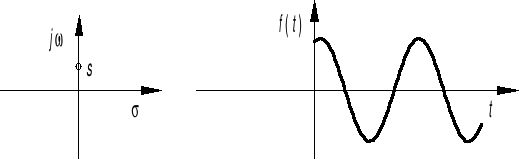
s j i σ 0
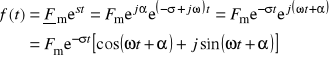
albo
![]()
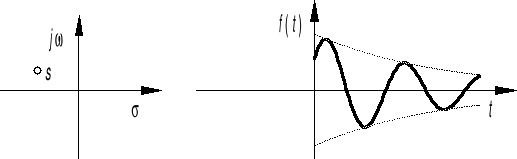
s j i σ > 0
![]()
albo
![]()
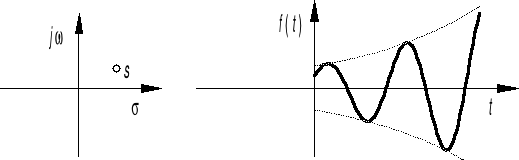
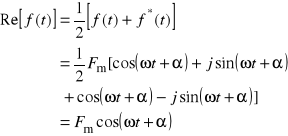
![]()
![]()
![]()
Elementy obwodu w dziedzinie częstotliwości uogólnionej
![]()
![]()
![]()
![]()
![]()
Metoda operatorowa. Transformacja
(przekształcenie) Laplace'a
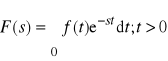
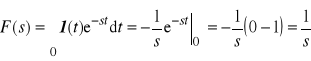
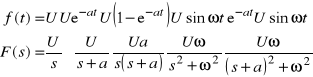
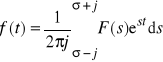
Prawo Ohma w postaci operatorowej
![]()
![]()
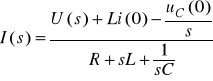
![]()
![]()
Gałąź szeregowa R i C
![]()
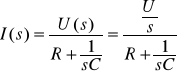
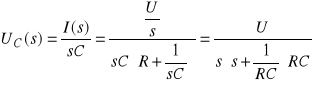
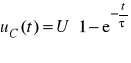
gdzie:
T RC — stała czasowa obwodu RC
Gałąź szeregowa R i L
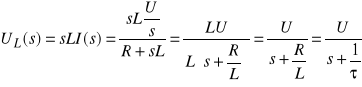
gdzie:
Z(s) R sL — impedancja operatorowa
T L/R — stała czasowa obwodu RL
![]()
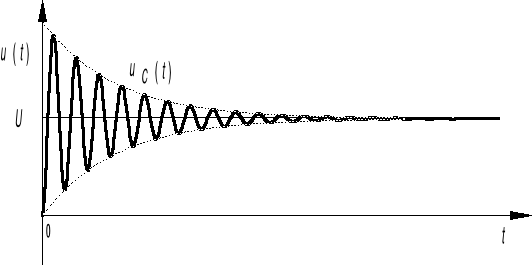
Gałąź szeregowa R, L i C
![]()
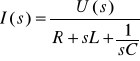
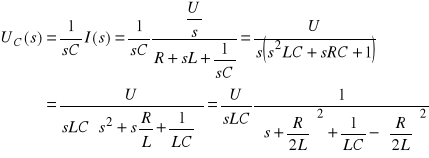
![]()
gdzie:
![]()
![]()
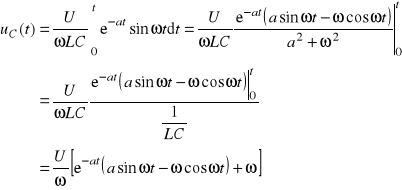
![]()
Wyszukiwarka
Podobne podstrony:
Koncepcja czestotliwosci zespolonejkolo, elektra, elektrotechnika gajusz, elektrotechnika gajusz, Wy
Koncepcja czestotliwosci zespolonej cdkolo, elektra, elektrotechnika gajusz, elektrotechnika gajusz,
Elektrostatyka 5kolo, elektra, elektrotechnika gajusz, elektrotechnika gajusz, Wykłady z elektry
Elektrodynamika cd4 kolo, elektra, elektrotechnika gajusz, elektrotechnika gajusz, Wykłady z elektry
Elektrodynamika cd4, elektra, elektrotechnika gajusz, elektrotechnika gajusz, Wykłady z elektry
Napiecie przemienne sinusoidalne cd4, elektra, elektrotechnika gajusz, elektrotechnika gajusz, Wykła
Elektromagnetyzm 3kolo, elektra, elektrotechnika gajusz, elektrotechnika gajusz, Wykłady z elektry
Napiecie przemienne sinusoidalne cd 3kolo, elektra, elektrotechnika gajusz, elektrotechnika gajusz,
Wielkosci fizyczne, elektra, elektrotechnika gajusz, elektrotechnika gajusz, Wykłady z elektry
Wyznaczanie zaciskow cewek jednoimiennychkolo, elektra, elektrotechnika gajusz, elektrotechnika gaju
Elektrostatyka 2kolo, elektra, elektrotechnika gajusz, elektrotechnika gajusz, Wykłady z elektry
Transformator jednofazowykolo, elektra, elektrotechnika gajusz, elektrotechnika gajusz, Wykłady z el
Elektromagnetyzm 8 koilo, elektra, elektrotechnika gajusz, elektrotechnika gajusz, Wykłady z elektry
Elektromagnetyzm 1 kolo, elektra, elektrotechnika gajusz, elektrotechnika gajusz, Wykłady z elektry
Wyznaczanie zaciskow cewek jednoimiennych, elektra, elektrotechnika gajusz, elektrotechnika gajusz,
Elektrodynamika cd3 kolo, elektra, elektrotechnika gajusz, elektrotechnika gajusz, Wykłady z elektry
więcej podobnych podstron