Część teoretyczna

Napięciem powierzchniowym można nazwać siły zmniejszające powierzchnię, które działają stycznie do powierzchni. Siły te są niezależne od wielkości powierzchni i zależą jedynie od charakteru cieczy oraz od temperatury. Napięcie powierzchniowe będące rezultatem oddziaływań międzycząsteczkowych maleje liniowo wraz ze wzrostem temperatury:

Molowa energia powierzchniowa jest to energia powierzchniowa 1 mola cieczy pod postacią kuli i wyrażamy ją wzorem:

Badania Eotvosa wykazały, że molowa energia powierzchniowa maleje wraz ze wzrostem temperatury i zależność ta jest liniowa aż do temperatury bliskiej temperatury krytycznej. Jak wynika doświadczenia, w temperaturze około 6°C niższej od temperatury krytycznej wartość napięcia powierzchniowego maleje do zera:

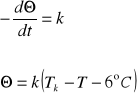
Zależność pomiędzy napięciem powierzchniowym cieczy a jej gęstością w stanie ciekłym i gazowym wykrył Baczyński:

Parachora jest to wielkość niezależna od temperatury i stała dla danej substancji. Wykazuje ona własności addytywne.

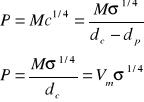
Celem mojego ćwiczenia było wyznaczenie wpływu temperatury na napięcie powierzchniowe cieczy. Pomiaru dokonałam metodą pęcherzykową, zwana też metodą maksymalnego ciśnienia baniek. Polega ona na pomiarze ciśnienia niezbędnego do przerwania błonki powierzchniowej przez pęcherzyk powietrza, który wydobywa się z kapilary. Stałość temperatury jest niezbędna do dokładnego wykonania pomiaru. Kapilara zanurzona jest do cieczy na pewna głębokość a z drugiej strony połączona jest z rurkami, przez które przeprowadzone jest powietrze do kapilary w celu wytworzenia pęcherzyka powietrza. Ważnym elementem jest manometr cieczowy zbudowany z dwóch rur o różnych promieniach. Zmiana położenia pęcherzyka powietrza w rurze poziomej jest proporcjonalna do zmiany poziomu cieczy wywołanej wytworzonym ciśnieniem w rurze pionowej.

Z uwagi na trudności eksperymentalne związane z bezpośrednim wyznaczeniem promienia kapilary r, w badaniach napięcia powierzchniowego stosuje się najczęściej metodę porównawczą. Przy użyciu tej samej aparatury wykonuje się pomiary z cieczą wzorcową o dokładnie znanym napięciu powierzchniowym. Stosując następując wzór do opisu napięcia powierzchniowego wody σ_w oraz cieczy badanej σ_x :

otrzymamy zależność:

Gdzie:

h_mw i h_mx- wskazania manometru odpowiednio, dla wody i cieczy badanej

h_rw i h_rx - głębokości zanurzenia kapilary w wodzie i cieczy badanej

d_rw i d_rx - gęstości wody i cieczy badanej.

Zatem, napięcie powierzchniowe cieczy badanej σ_x można obliczyć z równania:

Jest to najczęściej stosowany wzór, który pozwala wyznaczyć napięcie powierzchniowe cieczy badanej względem wzorca.

Część obliczeniowa

1. Obliczam napięcie powierzchniowe wody w t = 25°C :

= (75,92-0,163t_w)10^-3 [Nm^-1]

[Nm^-1]

2. Obliczam promień kapilary na podstawie wzoru:

[m]

[m]

[m]

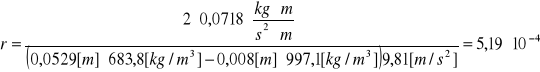
[m]

3. Obliczam wskazania manometru w czasie zanurzenia kapilary w cieczy badanej z zależności :

Dla t₁
[m]

Dla t₂
[m]

Dla t₃
[m]

Dla t₄
[m]

Dla t₅
[m]

Dla t₆
[m]

4.Obliczam gęstość 1,4-dioksanu we wszystkich badanych temperaturach z równania:

Dla t₁
[kg/m³]

Dla t₂
[kg/m³]

Dla t₃
[kg/m³]

Dla t₄
[kg/m³]

Dla t₅
[kg/m³]

Dla t₆
[kg/m³]

5. Obliczam napięcie powierzchniowe 1,4-dioksanu we wszystkich temperaturach pomiaru ze wzoru:

Dla t₁ :

Dla t₂
[Nm^-1]

Dla t₃
[Nm^-1]

Dla t₄
[Nm^-1]

Dla t₅
[Nm^-1]

Dla t₆
[Nm^-1]

6. Obliczam objętość molową 1,4-dioksanu we wszystkich temperaturach pomiaru korzystając z zależności:

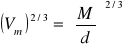
Dla t₁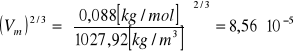
[m³/mol]

Dla t₂
[m³/mol]

Dla t₃
[m³/mol]

Dla t₄
[m³/mol]

Dla t₅
[m³/mol]

Dla t₆
[m³/mol]

7. Obliczam molową energię powierzchniową 1,4-dioksanu ze wzoru:

Dla t₁
[J/mol]

Dla t₂
[J/mol]

Dla t₃
[J/mol]

Dla t₄
[J/mol]

Dla t₅
[J/mol]

Dla t₆
[J/mol]

8. Po wykreśleniu zależności
obliczyłam stałą Eötvösa na podstawie metody graficznej:

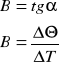
Wnioski

Wyznaczone przeze mnie stała Eötvösa wynosi:
. Wartość ta nie wiele różni się od wartości tablicowej:
. Wykonane przeze mnie doświadczenie potwierdza fakt, że temperatura wpływa na wartość napięcia powierzchniowego, a mianowicie napięcie maleje liniowo wraz ze wzrostem temperatury.

---