Wykłady n.t.
Teoretyczne podstawy informatyki
Algebra Boole'a
Zbiór wartości z określonymi w nich działaniami na dwóch elementach: mnożenia ∧ i dodawania ∨ i działania na jednym elemencie : dopełnienie ~
Dwa wyróżnione elementy 0 i 1 , w których są spełnione aksjomaty dla wszystkich elementów o symbolach x, y, z ∈ {0, 1 }
A1: x ∨ 0 = x A2: x ∧ 1 = x moduł sumy i mnożenia
A3: x ∨ y = y ∨ x A4: x ∧ y = y ∧ x przemienność działania
A5: x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z) rozdzielność dodawania względem mnożenia
A6: x ∧ (y ∨ z) = (x ∧ y) ∨ (x ∧ z) rozdzielność mnożenia względem dodawania
A7: x ∨ ~x = 1 A8: x ∧ ~x = 0
A9: x ∧ ( y ∧ z ) = ( x ∧ y ) ∧ z łączność mnożenia
A10: x ∨ ( y ∨ z ) = ( x∨ y ) ∨ z łączność dodawania
dodatkowo dodaje się najczęściej aksjomaty:
x ∨ 1 = 1 x ∧ 0 = 0 A.11 i A.12
można zamiast tych aksjomatów podać dwa inne
x ∨ 1 = ~x x ∧ 0 = ~x A.13 i A.14
W przypadku przyjęcia aksjomatów A.11 i A.12 otrzymujemy następujące tabele zależności (czasami nazywamy je tabelami prawdy):
x |
y |
F(x,y) = x ∨ y |
|
x |
y |
F(x,y) = x ∧ y |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
W przypadku przyjęcia aksjomatów A.13 i A.14 otrzymalibyśmy tabele zależności
x |
y |
F(x,y) = x ∨ y |
|
x |
y |
F(x,y) = x ∧ y |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
Funkcja boole'owska
Funkcja boole'owska odwzorowuje zbiory wartości boole'owskich w zbiór wartości boole'owskich:
F(a,b,c,...) z, gdzie a, b, c, ... , z ∈ {0,1}
Funkcje takie można opisać w trojaki sposób:
słowny,
w postaci tabeli zależności,
w postaci wyrażeń boole'owskich
Implikanty i implicenty
Implikantem funkcji F() nazywamy iloczyn I zmiennych w postaci prostej lub zanegowanej, spełniający następującą zależność:
I=1 ⇒ F()=1
Implikant zawierający wszystkie zmienne funkcji F nazywamy implikantem pierwotnym.
Implikant funkcji F, z którego usunięcie dowolnej zmiennej powoduje, że przestaje być implikantem nazywamy implikantem prostym.
Implicentem funkcji F() nazywamy sumę J zmiennych w postaci prostej lub zanegowanej, spełniającą następującą zależność:
J=0 ⇒ F()=0
Implicent zawierający wszystkie zmienne funkcji F nazywamy implicentem pierwotnym.
Implicent funkcji F, z którego usunięcie dowolnej zmiennej powoduje, że przestaje być implicentem nazywamy implicentem prostym.
Przekształcanie i upraszczanie formuł boole'owskich
Prawa d'Morgana
~(x ∧ y) = ~x ∨ ~y oraz ~(x ∨ y) = ~x ∧ ~y
Reguła pochłaniania
A ∨ (A ∧x) = A ∨ (A ∧~x) = A
oraz
A ∧ (A ∨ x) = A ∧ (A ∨ ~x) = A
Reguła sklejania
(A ∧~x) ∨ (A ∧x) = A
oraz
(A ∨ ~x) ∧ (A ∨ x) = A
Sąsiedztwo logiczne
Sąsiedztwo słów binarnych:
Dwa słowa binarne o tej samej długości (ta sama liczba bitów) są sąsiednie logicznie jeżeli różnią się tylko na jednej pozycji.
Sąsiedztwo implikantów (implicentów):
Każdy pierwotny implikant (implicent) można zapisać w postaci ciągu zer i jedynek, przypisując zmiennej w postaci prostej jedynkę a zmiennej w postaci zanegowanej zero lub odwrotnie. Zatem analogicznie do sąsiedztwa słów binarnych, dwa pierwotne implikanty (implicenty) są sąsiednie logicznie jeżeli różnią się postacią tylko jednej zmiennej.
Synteza i upraszczanie funkcji boole'owskiej
Sposoby opisu funkcji boole'owskiej:
opis słowny,
opis w postaci tablicy zależności,
opis w postaci wyrażenia algebraicznego.
W dalszej części przyjmuje się następujące oznaczenia:
~x oznaczamy
~(x ∧ y) oznaczamy
~( x ∨ y ) oznaczamy
Tabela 1
waga/ równoważnik |
a |
b |
c |
d |
F1 |
F2 |
F3 |
f |
f |
f |
f |
f |
f |
f |
f |
f |
f |
f |
f |
f |
f |
f |
f |
|
23 |
22 |
21 |
20 |
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
9 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
10 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
11 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
12 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
13 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
14 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
15 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
F1 = f0 + f2 + f5 + f8 + f9 + f11 + f12 + f13 + f15 = ….
F2 = f0 + f1 + f3 + f4 + f6 + f7 + f11 + f12 + f13 + f14 = …
F3 = f1 + f3 + f6 + f9 + f10 + f15 = ....
Tabela 1
waga/ równoważnik |
a |
b |
c |
d |
F1 |
F2 |
F3 |
g |
g |
g |
g |
g |
g |
g |
g |
g |
g |
g |
g |
g |
g |
g |
g |
|
23 |
22 |
21 |
20 |
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
3 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
5 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
6 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
7 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
8 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
10 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
11 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
12 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
13 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
14 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
15 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
F1 = g1 * g3 * g4 * g6 * g7 * g10 * g14 = ...
F2 = g2 * g5 * g8 * g9 * g10 * g15 = ...
F3 = g0 * g2 * g4 * g5 * g8 * g11 * g12 * g13 * g14 = ...
Przykład przekształcania funkcji boole'owskiej do postaci kanonicznej
Przekształćmy do postaci kanonicznych: sumy iloczynów i iloczynu sum funkcję:
Wykorzystując prawa de Morgana otrzymamy:
W celu otrzymania postaci sumy iloczynów wykorzystamy prawo rozdzielności mnożenia względem dodawania. Otrzymamy wówczas:
W celu otrzymania postaci iloczynu sum wykorzystamy prawo rozdzielności dodawania względem mnożenia. Otrzymamy wówczas:
Siatki Karnaugh'a - upraszczanie funkcji logicznej
Zapis informacji - kodowanie liczb
kodowanie znaków np. ASCII
kodowanie liczb
liczby stałopozycyjne
znak - moduł (0 - liczba dodatnia, 1 - ujemna)
Przykład 0 001011 odpowiada +11
1 010101 odpowiada - 21
moduł
znak
uzupełnienie do 1
Przykład 0 001011 odpowiada +11
negacja wszystkich bitów
1 110100 odpowiada -11
0 010101 odpowiada +21
1 101010 odpowiada - 21
pozostała część zapisu
znak
uzupełnienie do 2
Przykład 0 001011 odpowiada +11
negacja wszystkich bitów - uzupełnienie do 1
1 110100 odpowiada -11
+1
1 110101 uzupełnienie do 2
pozostała część zapisu
znak
0 011100 odpowiada +28
1 100011 uzupełnienie do 1
1 100100 odpowiada - 28 uzupełnienie do 2
pozostała część zapisu
znak
! W zapisie uzupełnienia do 1 wartość 0 reprezentują dwie postaci 0 000000 (+0) i 1 111111 (-0)
! Liczby dodatnie w zapisie uzupełnienie do 1 i do 2 są zgodne z zapisem znak moduł
! Najstarszy bit zapisu U1 i U2 wskazuje na znak liczby
kodowanie ósemkowe {0,1,2,3,4,5,6,7} odpowiada {000,001,010,011,100,101,110,111}
kodowanie szesnastkowe {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}
kodowanie dwójkowo - dziesiętne (BCD, kody refleksyjne, kod Exess 3)
liczby zmiennopozycyjne : zapis znak cecha mantysa
Kody dwójkowo dziesiętne
Liczba przedstawiana jest w postaci dwójkowo-dziesiętnej, tzn. każda pozycja dziesiętna zapisana jest w postaci binarnej (jeden z kodów dwójkowo - dziesiętnych)
Kod dziesiętny |
Kod 8421 |
Kod Excess 3 |
Kod 2421 |
0 |
0 0 0 0 |
0 0 1 1 |
0 0 0 0 |
1 |
0 0 0 1 |
0 1 0 0 |
0 0 0 1 |
2 |
0 0 1 0 |
0 1 0 1 |
0 0 1 0 |
3 |
0 0 1 1 |
0 1 1 0 |
0 0 1 1 |
4 |
0 1 0 0 |
0 1 1 1 |
0 1 0 0 |
5 |
0 1 0 1 |
1 0 0 0 |
1 0 1 1 |
6 |
0 1 1 0 |
1 0 0 1 |
1 1 0 0 |
7 |
0 1 1 1 |
1 0 1 0 |
1 1 0 1 |
8 |
1 0 0 0 |
1 0 1 1 |
1 1 1 0 |
9 |
1 0 0 1 |
1 1 0 0 |
1 1 1 1 |
Najkorzystniejszy z punktu widzenia operacji sumowania jest kod Excess 3.
Przykład
2 3 5 0010 0011 0101 0101 0110 1000
1 7 2 0001 0111 0010 0100 1010 0101
4*0 7 0011 1010 0111 1010*0000 1101
korekta 0100*0000 - 11 +11 - 11
0100 0000 0111 0111 0011 1010
Kod Grey'a
Kolejne słowa kodowe różnią się jednym bitem (na jednej pozycji)
**0 0000
**1 0001
*11 0011
*10 0010
110 0110
111 0111
101 0101
100 0100
1100
1101
1111
1110
1010
1011
1001
1000
Kody detekcyjno - korygujące
Stosowane w celu zwiększenia odporności na zakłócenia przy przesyłaniu informacji cyfrowej na odległość.
Ze zbioru możliwych liczb binarnych (najczęściej o stałej długości) wybrana jest pewna grupa. Pozostałe liczby uważane są za zakazane.
Wyróżnia się:
kody liniowe z wyróżnionymi grupami parzystości (np. kod z bitem parzystości) oraz
kody ze stałą liczbą jedynek (najczęściej dwoma)
Dodawanie i odejmowanie liczb binarnych
Reguły wykonywania operacji dodawania i odejmowania
|
znak - moduł |
uzupełnienie do jedności |
uzupełnienie do dwóch |
A > 0 B > 0 |
dodać liczby i przepisać znak 0 |
||
A < 0 B < 0 |
- przepisać znak 1 |
|
|
A*B<0 |
Uwaga: w dodawaniu nie bierze udziału bit znaku |
|
|
Postać zmiennoprzecinkowa
Postać w systemie dziesiętnym:
A = m * 10 c
Przykład
0.453 * 10-12 zapisana numerycznie 0.453E-12
Postać znormalizowana posiada następujące właściwości:
110 > m ![]()
0.110 oraz
c jest liczbą całkowitą
Postać w systemie dwójkowym:
A = m * 2 c
gdzie: 12 > m ![]()
0.12 oraz
W tym przypadku po przecinku (kropce) zawsze będzie występowała jedynka. Dla oszczędności można tą pozycję pominąć.
Postać binarna:
bit znaku |
|
cecha w zapisie uzupełnienia do 2 |
|
1 |
|
mantysa (bity umieszczone po kropce) |
|
Mnożenie i dzielenie liczb binarnych
Przesuwanie liczb ze znakiem
Przesuwanie liczb jest jednoznaczne z mnożeniem danej liczby przez 2i (gdy przesuwamy liczbę mnożoną przez 2i w lewo o "i" pozycji) i dzieleniem, czy też mnożeniem przez 2-i (gdy przesuwamy liczbę mnożoną przez 2-i w prawo o "i" pozycji.)
Tabela 1. Przesuwanie liczb
Liczba dodatnia i ujemna w kodzie ZM |
znak bez zmian |
przy przesunięciu wszystkie dodane cyfry są zerami |
Liczba dodatnia i ujemna w postaci kodu ZU1 |
|
przy przesunięciu wszystkie cyfry dodane odpowiadają bitowi znaku |
Liczba dodatnia i ujemna w postaci kodu ZU2 |
|
przy przesunięciu w lewo dodajemy zera przy przesunięciu w prawo dodajemy cyfry odpowiadające bitowi znaku |
Ilustracja graficzna
Zapis znak moduł
PRZYKŁAD:
D(A) = (-10)10
Kod Znak - Moduł ZM
1.01010 * 21 = 1.10100 = -20
1.01010 * 2-1 = 1.00101 = -5
Zapis uzupełnienie do jedności
PRZYKŁAD:
D(A) = (-10)10
Kod ZU1
1.10101 * 21 = 1.01011 = -20
1.10101 * 2-1 = 1.11010 = -5
Zapis uzupełnienia do dwóch
PRZYKŁAD:
D(A) = (-10)10
Kod ZU2
1.10110 * 21= 1.01100 = -25 + 23 + 22 = -32 + 8 + 4 = -20
1.10110 * 2-1= 1.11011 = -25 + 24 + 23 + 21 + 20 = -32 + 27 = -5
METODY MNOŻENIA LICZB W SYSTEMIE DWÓJKOWYM
Mnożenie można przeprowadzić wykorzystując metody:
metoda mnożenia bezpośredniego,
metoda Burksa - Goldsteine'a - von Neumanna,
I metoda Robertsona,
II metoda Robertsona,
metoda Bootha.
METODA MNOŻENIA BEZPOŚREDNIEGO
Jest stosowana do liczb zapisanych w kodzie ZM. Mnożenie w tej metodzie przebiega tak jak mnożenie pisemne liczb dziesiętnych, zatem jest ono zastąpione wielokrotnym dodawaniem odpowiednio przesuniętej mnożnej.
MNOŻENIE METODĄ BOOTH'A
I wariant metody Booth'a
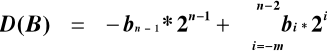
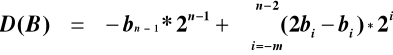
![]()
![]()
![]()
![]()
Współczynnik ![]()
nie występuje we wzorze pierwszym, zatem jest równy 0.
Porównywanie par bitów mnożnika (w ZU2). Badamy ostatnie pary bitów (cyfr) mnożnika.
Jeżeli badana para jest kombinacją 1 0, to od iloczynu częściowego odejmujemy mnożną D(A) i przesuwamy wynik o jedno miejsce w prawo (*2-1).
Jeżeli badana para jest odpowiednio parą 0 1, to dodajemy mnożną do iloczynu częściowego i przesuwamy cały wynik o jedno miejsce w prawo.
Jeżeli badana para jest parą o jednakowych cyfrach 0 0 lub 1 1, to wykonujemy tylko przesunięcie w prawo.
Jeżeli w skład wchodzi bit znakowy (znak), to nie wykonujemy przesunięcia.
PRZYKŁAD 1:
Dla I wariantu metody Booth'a
D(A) = ![]()
= (0.00111)ZM
D(B)= 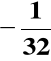
= (1.00001)ZM = (1.11111)ZU2
Do liczby B na najmniej znaczącej pozycji dopisujemy 0, zatem:
D(B) = (1.111110)ZU2
Badamy kolejne bity mnożnika (czyli kolejne bity liczby B):
para 1-0 - od iloczynu częściowego odejmujemy mnożną (iloczyn częściowy wynosi na początku 0), następnie przesuwamy wynik o jedno miejsce w prawo,
para 1-1 - przesuwamy iloczyn częściowy o jedno miejsce w prawo,
para 1-1 - przesuwamy iloczyn częściowy o jedno miejsce w prawo,
para 1-1 - przesuwamy iloczyn częściowy o jedno miejsce w prawo,
para 1-1 - przesuwamy iloczyn częściowy o jedno miejsce w prawo.
para 1-0 - od iloczynu częściowego odejmujemy mnożną (iloczyn częściowy wynosi na początku 0), następnie przesuwamy wynik o jedno miejsce w prawo,
para 0-1 - do iloczynu częściowego dodajemy mnożną, przesuwamy iloczyn częściowy o jedno miejsce w prawo,
para 0-0 - przesuwamy iloczyn częściowy o jedno miejsce w prawo,
para 1-0 - od iloczynu częściowego odejmujemy mnożną, przesuwamy iloczyn częściowy o jedno miejsce w prawo,
para 0-1 - do iloczynu częściowego dodajemy mnożną, przesuwamy iloczyn częściowy o jedno miejsce w prawo.
Przesuwamy mnożną o jedno miejsce w prawo (uzyskujemy A/2 - “A - pół”).
Zbadamy ostatni bit mnożnika, jeżeli jest on równy 1, to dodajemy mnożną do iloczynu częściowego, który jest równy zeru na początku mnożenia, jeżeli ostatni bit mnożnika jest równy 0, to nie wykonujemy żadnego działania.
Przesuwamy iloczyn częściowy o jedno miejsce w prawo.
Przesuwamy mnożnik o jedno miejsce w prawo ( przejście do kolejnego badania bitu mnożnika). Jeżeli badany bit jest bitem znakowym b0, to wtedy gdy jego wartość wynosi 1 odejmujemy mnożną od iloczynu częściowego, zaś gdy jest on równy 0 nie wykonujemy żadnego działania.
Uzyskany iloczyn częściowy przesuwamy o jedno miejsce w lewo (powrót do A), wynik jest w postaci ZU2.
bit = 1 - dodajemy mnożną (“A-pół”) do iloczynu częściowego (na początku równego 0), a następnie przesuwamy otrzymany iloczyn częściowy o jedno miejsce w prawo,
bit = 0 - nie wykonujemy żadnej operacji, przesuwamy otrzymany iloczyn częściowy o jedno miejsce w prawo,
bit = 1 - dodajemy mnożną do iloczynu częściowego, przesuwamy otrzymany iloczyn częściowy o jedno miejsce w prawo,
bit = 1 - dodajemy mnożną do iloczynu częściowego, przesuwamy otrzymany iloczyn częściowy o jedno miejsce w prawo,
bit = 0 - nie wykonujemy żadnej operacji, przesuwamy iloczyn częściowy o jedno miejsce w prawo,
bit =1 - badany bit jest bitem znakowym i jest równy 1 dlatego wystąpi tzw. poprawka - odejmujemy mnożną od iloczynu częściowego,
otrzymany wynik przesuwamy o jedno miejsce w lewo.
metoda porównawcza,
metoda restytucyjna,
metoda nierestytucyjna,
Jeżeli dzielnik jest mniejszy od rn-tej reszty rn=>B, to odejmujemy dzielnik od przesuniętej n - tej reszty, a bit ilorazu qi = 1.
Jeżeli n - ta reszta jest mniejsza od dzielnika rn<B, to kolejny bit ilorazu qi = 0. Następnie przesuwamy wynik o jedno miejsce w lewo. Otrzymaną resztę częściową porównujemy z dzielnikiem.
dla problemów decyzyjnych,
dla problemów optymalizacyjnych.
Łańcuch symboli kodujących dane konkretnego problemu nie może zawierać nadmiarowych symboli,
Liczby występujące w danych powinny być zapisane dwójkowo lub przy użyciu dowolnej innej ustalonej podstawie liczenia większej od 1.
maszyna o dostępie swobodnym RAM - random acces machine
maszyna Turinga
skończonego alfabetu symboli;
skończonego zbioru stanów;
nieskończonej taśmy z zaznaczonymi kwadratami, z których każdy może zawierać pojedynczy symbol;
ruchomej głowicy odczytująco - zapisującej, która może wędrować wzdłuż taśmy przesuwając się na raz o jeden kwadrat
diagramu przejść między stanami, zawierającego instrukcje, które powodują, że zmiany następują przy każdym zatrzymaniu się.
zmienia stan,
wpisuje symbol w obserwowanej komórce taśmy, zastępując symbol tam wpisany,
przesuwa głowicę o jedną komórkę w prawo lub w lewo.
dla danego stanu qi kolejny stan qi+1
symbol, który ma być zapisany na taśmie
kierunek (L / P) dla ruchu głowicy
Gramatyki klasy φ
Gramatyki klasy 1 (kontekstowe):
Gramatyki klasy 2 (bezkontekstowe):
Gramatyki klasy 3 (regularne):
nawias otwierający zawsze wprowadzany jest do stosu.
argumenty wyprowadzane są bezpośrednio na wyjście stosu.(nie „wchodzą” do stosu).
operator wprowadzany jest do stosu, o ile ma wyższy priorytet od operatora znajdującego się na szczycie stosu.
jeżeli operator ma równy lub niższy priorytet niż operator znajdujący się na szczycie stosu, to wówczas wprowadzany jest do stosu , usuwając przedtem z niego wszystkie operatory o równym i niższym priorytecie,
nawias zamykający powoduje wyprowadzenie zawartości stosu do pierwszego napotkanego nawiasu otwierającego, łącznie z nim.
Krok 1 |
|
0 00000 |
|
|
- 1 11001 |
|
|
1 11001 |
|
|
1 111001 |
Krok 2 |
|
1 1111001 |
Krok 3 |
|
1 11111001 |
Krok 4 |
|
1 111111001 |
Krok 5 |
|
1 1111111001 |
Wynik:
(1.1111111001)ZU2 = (1.0000000111)ZM = 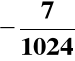
PRZYKŁAD 2:
Dla I wariantu metody Booth'a
D(A) = 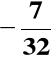
= (1.00111)ZM = (1.11001)
D(B) = ![]()
= (0.01001)ZM = (0.01001)ZU2
Do liczby B na najmniej znaczącej pozycji dopisujemy 0, zatem:
D(B) = (0.010010)ZU2
Badamy kolejne bity mnożnika (czyli kolejne bity liczby B):
Krok 1 |
|
0 00000 |
|
|
- 0 00111 |
|
|
0 00111 |
|
|
0 000111 |
Krok 2 |
|
+1 11001 |
|
|
1 111001 |
|
|
1 1111001 |
Krok 3 |
|
1 11111001 |
Krok 4 |
|
- 0 00111 |
|
|
0 00110001 |
|
|
0 000110001 |
Krok 5 |
|
+1 11001 |
|
|
1 111000001 |
|
|
1 1111000001 |
Wynik:
(1.1111000001)ZU2 = (1.0000111111)ZM = 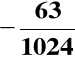
II wariant metody Booth'a:
PRZYKŁAD:
Dla II wariantu metody Booth'a
D(A) = ![]()
= (0.11001)ZM
D(B) = 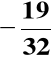
= (1.10011)ZM = (1.01100)ZU1 = (1.01101)ZU2
Przesuwamy mnożną o jedno miejsce w prawo - uzyskanie wartości “A - pół”:
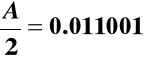
Badamy kolejne bity mnożnika począwszy od ostatniego:
Krok 1 |
|
0 000000 |
|
|
+0 011001 |
|
|
0 011001 |
|
|
0 0011001 |
Krok 2 |
|
0 00011001 |
Krok 3 |
|
+0 011001 |
|
|
0 01111101 |
|
|
0 001111101 |
Krok 4 |
|
+0 011001 |
|
|
0 101000101 |
|
|
0 0101000101 |
Krok 5 |
|
0 00101000101 |
Krok 6 |
|
-1 100111 |
|
|
1 11000100101 |
|
|
1 1000100101 |
Wynik: (1.1000100101)ZU2 = (1.0111011011)ZM = ![]()
Uwaga:
Mnożymy nie tylko ułamki!
Jeżeli chcemy pomnożyć ułamki niewłaściwe to możemy zapisać je w postaci mantysy i cechy i wykonujemy mnożenie mantys i dodawanie cech, ostateczny wynik to mantysa * 2cecha.
Innym rozwiązaniem jest ustalenie pozycji części ułamkowych mnożnej i mnożnika. Wówczas w ostatecznej postaci wyniku należy wyznaczyć dodatkowo położenie części ułamkowej wyniku.
DZIELENIE LICZB BINARNYCH
Dzielenie można przeprowadzić wykorzystując następujące metody:
Metoda porównawcza - jest stosowana w zapisie znak moduł (ZM) i gdy jest spełniony warunek A<B, gdzie:
A - dzielna
B - dzielnik
r0 - reszta początkowa
Rn - reszta z dzielenia
rn - n - ta reszta częściowa
Q - iloraz uzyskany w algorytmie o bitach qi.
Metoda ta polega na porównywaniu dzielnika z n - tą resztą.
Uwaga: Wynikiem dzielenia jest iloraz Q o bitach q0q1..qi.W pierwszym kroku porównujemy resztę początkową r0 z dzielnikiem, gdzie r0 - to D(A) zapisana na tylu pozycjach co D(B).
PRZYKŁAD:
Dla metody porównawczej
A= 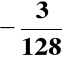
= (1.0000011)ZM
B = ![]()
= (0.1001)ZM
Warunek A<B jest spełniony; porównujemy kolejne reszty częściowe z modułem dzielnika:
Krok I: r0 A<B |
|
.0000011 |
|
|
|
.0000110 |
|
Krok II: r1 <B |
r1 = |
.0000110 |
|
|
|
.0001100 |
|
Krok III: r2 <B |
r2 = |
.0001100 |
|
|
|
.0011000 |
|
Krok IV: r3 <B |
r3 = |
.0011000 |
|
|
|
.0110000 |
|
Krok V: r4 <B |
r4 = |
.0110000 |
|
|
|
.1100000 |
|
Krok VI: r5 >B |
r4 = |
.1100000 |
|
|
|
-.1001000 |
|
|
|
.0011000 |
|
|
|
.0110000 |
|
reszta z dzielenia Rn wyraża się wzorem:
Rn = ![]()
Rn = 0.011 * 101.110 (uwaga! wynik jest zapisany binarnie)
Bit znaku q0 = a0 A b0, czyli q0 = 1, bo a0 = 1, b0 = 0
Ostateczny iloraz Q wynosi: Q = q0 q1 q2...qn = 1.00001
Metoda restytucyjna -
to metoda dzielenia dwóch liczb zapisanych w kodzie znak moduł (ZM) i gdy |A|<|B|.
Algorytm metody restytucyjnej różni się od metody porównawczej tym, że zawsze następuje odejmowanie dzielnika od i - tej reszty. Jeżeli otrzymana reszta jest większa od zera, to kolejny bit ilorazu jest równy 1, jeżeli jest mniejsza od zera, to kolejny bit ilorazu jest równy 0. Bez względu na znak reszty z odejmowania przesuwamy resztę o jedno miejsce w lewo. Dla reszty ujemnej z powrotem dodajemy dzielnik, zanim przesuniemy wynik w lewo.
Metoda nierestytucyjna -
to metoda dla dzielenia dwóch liczb zapisanych w kodzie ZU2. Dzielna A i dzielnik B są ułamkami w postaci znormalizowanej oraz wymagane jest by był spełniony warunek |A|<|B|.
Metoda ta polega na badaniu znaku dzielnika i kolejnej reszty częściowej. Jeżeli znaki są zgodne to odejmujemy dzielnik od przesuniętej w lewo kolejnej reszty częściowej. Jeżeli znaki ich są różne to dodajemy dzielnik do przesuniętej w lewo kolejnej reszty częściowej. Przy zgodnych bitach znakowych dzielnika i reszty bit ilorazu jest równy 1, a dla znaków przeciwnych jest równy 0. Do otrzymanego wyniku dodajemy poprawkę równą: -1+2-n, gdzie n - oznacza n - tą resztę z dzielenia.
PRZYKŁAD:
Dla metody nierestytucyjnej
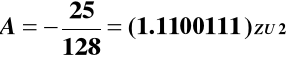
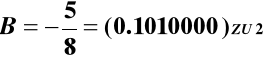
1.0110000 !!!!
Warunek ![]()
jest spełniony:
r0 |
1.1100111 |
q0 = 1 |
|
1.100111 |
|
|
- 1.0110000 (+0.1010000) |
|
r1 |
0.0011110 |
q1 = 0 |
|
0.01111 |
|
|
+1.0110000 |
|
r2 |
1.11011 |
q2 = 1 |
|
1.1011 |
|
|
-1.0110000 (+0.1010000) |
|
r3 |
0.0101 |
q3 = 0 |
|
0.101 |
|
|
+1.0110000 |
|
|
0.000 |
|
nastąpiło wyzerowanie reszty częściowej. Koniec obliczeń.
Wynik: 1.010;
Do wyniku dodajemy poprawkę, która wynosi:
-1 + 2-n, gdzie n jest to nr ostatniej reszty dzielenia, zatem:
-1 + 2-n = (1.0001)ZU2
Q = 1.010 +1.0001 = (0.0101)ZU2 = + ![]()
Algorytmy
W sposób nieformalny możemy określić algorytm jako ściśle określoną procedurą obliczeniową, która dla poprawnych danych wejściowych „wytwarza” żądane dane wyjściowe nazywane wynikiem działania algorytmu. Algorytm jest więc ciągiem kroków obliczeniowych prowadzących do przekształcenia danych wejściowych w wyjściowe.
Inaczej, algorytm można potraktować jako sposób rozwiązania konkretnego problemu obliczeniowego. Postawienie problemu polega na sprecyzowaniu wymagań dotyczących relacji między danymi wejściowymi i wyjściowymi, a algorytm opisuje właściwą procedurę obliczeniową, która zapewnia, że ta relacja zostaje osiągnięta.
Algorytm jest poprawny, gdy dla każdego egzemplarza problemu algorytmu zatrzymuje się i daje poprawny wynik. Mówimy wtedy, że poprawny algorytm „rozwiązuje” zadany problem obliczeniowy. Algorytm niepoprawny może się nigdy nie zatrzymać albo po zatrzymaniu dać wynik zły. Niepoprawne algorytmy mogą być jednak użyteczne, jeśli ich błędne działanie może być kontrolowane.
Algorytm może być przedstawiany w postaci programu komputerowego albo zrealizować sprzętowo. Jedynym wymaganiem jest precyzja opisu wynikającej z niego procedury obliczeniowej.
Złożoność obliczeniowa algorytmów
Algorytmy:
Problemy decyzyjne - problemy, na które można dać odpowiedź tak lub nie.
Np. problemy z dziedzin: teorii liczb, teorii grafów, teorii automatów
Problemy optymalizacyjne - ekstremalizacja pewnej funkcji celu.
W sensie „natury obliczeniowej” można badać w ten sam sposób co problemy decyzyjne. Problem optymalizacyjny można sprowadzić do problemu decyzyjnego. Taki problem decyzyjny nie jest obliczeniowo trudniejszy niż odpowiadający mu problem optymalizacyjny.
Jeśli problem decyzyjny jest obliczeniowo „trudny” (NP.-zupełny), to trudny jest również problem optymalizacyjny.
Teoria złożoności obliczeniowej
W odniesieniu do problemów decyzyjnych.
Pytanie: czy dla rozważanego problemu istnieje w ogóle jakiś rozwiązujący go algorytm (tzn. procedura pozwalająca dać odpowiedź tak lub nie).
Odpowiedź, to stwierdzenie czy problem jest rozstrzygalny czy nierozstrzygalny.
Postulat rozróżniania algorytmów lepszych i gorszych z obliczeniowego punktu widzenia: czas i zajętość pamięci.
Istnieje wiele algorytmów, dla których nie udało się podać „dobrych” algorytmów, ale sprowadzają się te problemy do siebie nawzajem, tak że znając rozwiązanie jednego z nich, można w wielomianowym czasie skonstruować rozwiązanie innego.
Definicja
Przez problem Π rozumiany będzie zbiór parametrów, które nie muszą mieć nadanych wartości, oraz zdanie określające właściwości jakie powinno mieć rozwiązanie tego problemu.
Ustalając wartości wszystkich parametrów problemu Π otrzymamy konkretny problem (instalację) I.
Zbiór wszystkich konkretnych problemów oznaczamy przez DΠ .
Dane konkretnego I є DΠ , kodowane są za pomocą skończonego łańcucha x(I) symboli należących do z góry określonego alfabetu Σ zgodnie z ustalonymi regułami kodowania.
Rozmiar konkretnego problemu N(L), to długość łańcucha danych x(I).
Reguły kodowania powinny spełniać następujące postulaty:
Można przyjąć każdą „rozsądną” regułę kodowania, która nie powoduje wykładniczego wzrostu rozmiaru kodowania konkretnego problemu w stosunku do innych reguł kodowania.
W praktyce dogodne jest wyrażanie rozmiaru problemu za pomocą jednego parametru, określającego liczbę elementów zbioru charakterystycznego dla danych rozważanego konkretnego problemu. Np. dla określenia maksymalnego przepływu w sieciach - liczba wierzchołków w sieci.
Problemowi decyzyjnemu Π i regule kodowania e odpowiada język L(Π,e) = {x(I) є Σ*: I є DΠ ∧ Σ jest alfabetem używanym przez e ∧ odpowiedź na I brzmi „tak”}.
Σ* - zbiór wszystkich skończonych łańcuchów symboli należących do Σ
Rozwiązania problemu Π odpowiada rozpoznanie języka L(Π,e)
Algorytm rozwiązuje problem Π, jeśli znajduje rozwiązanie dla każdego konkretnego problemu I є DΠ
Definicja
Funkcja f(k) jest rzędu g(k), co zapisuje się O(g(k)), jeśli istnieje taka stała c, że | f(k) | <= c * | g(k) |, dla wszystkich wartości k
Definicja
Funkcja złożoności obliczeniowej algorytmu A rozwiązującego problem Π będziemy rozumieli funkcję złożoności czasowej przyporządkowującą każdej wartości rozmiaru konkretnego problemu I є DΠ maksymalną liczbę elementarnych kroków maszyny cyfrowej potrzebnych do rozwiązania za pomocą algorytmu A konkretnego problemu o tym rozmiarze, tzn. funkcję
fA(N(I)) = max{t: t jest liczbą elementarnych kroków niezbędnych dla rozwiązania konkretnego problemu I є DΠ ∧ |x(I)| = N(I)}
Można udowodnić, że wybór konkretnej reguły kodowania i modelu maszyny cyfrowej nie ma wpływu na rozróżnienie między algorytmami wielomianowymi i wykładniczymi.
Definicja
Algorytmem wielomianowym nazywamy algorytm, którego funkcja złożoności obliczeniowej jest O(p(k)), gdzie p jest pewnym wielomianem, a k rozmiarem rozwiązywanego konkretnego problemu.
Każdy algorytm, którego funkcja złożoności nie może być tak ograniczona, nazywa się algorytmem wykładniczym. !Funkcja złożoności obliczeniowej tych algorytmów nie musi być funkcją wykładniczą!
Algorytmy wielomianowe - efektywne
Algorytmy wykładnicze - nie efektywne
Klasy złożoności obliczeniowej
Uogólnione modele maszyn cyfrowych:
Rysunek 1. Podstawowy model maszyny RAM
Maszyna Turinga
Maszyna Turinga jest prostym urządzeniem algorytmicznym, uderzająco prymitywnym w porównaniu z dzisiejszymi komputerami i językami programowania, a jednak na tyle efektywnym, że pozwala na wykonanie nawet najbardziej złożonych algorytmów. Maszyna Turinga jest mechanizmem powstałym w wyniku ciągu uproszczeń: danych, sterowania nimi oraz uproszczeń podstawowych operacji. Maszynę tą wymyślił w roku 1936 brytyjski matematyk A.M.Turing
Wprowadzenie takiego prostego i stosunkowo powolnego modelu obliczeń ma swoje uzasadnienie. Używać go bowiem będziemy wtedy, gdy problem będzie miał złożoność obliczeniową „wyższego rzędu”.
Zasady zapisu algorytmów w Maszynie Turinga:
Zasada 1: Upraszczanie danych
Każdy element danych używany w algorytmie, czy to będą dane wejściowe, wyjściowe czy wartości pośrednie, można traktować jako ciąg symboli, czyli napis. Liczba całkowita nie jest niczym innym, jak ciągiem cyfr, liczba ułamkowa zaś ciągiem cyfr, który może zawierać kropkę. Prostej linearyzacji mogą podlegać zarówno słowa jak i teksty, które są ciągiem symboli składającym się z liter, znaków przestankowych i odstępów. Wszystkie obiekty a nawet najbardziej skomplikowane struktury danych możemy łatwo zakodować, traktując je cały czas symbolicznie, jako liczby, słowa lub teksty.
Liczba różnych symboli jest skończona i ustala się ją zawczasu. Każdą interesującą nas jednostkę danych możemy więc zapisać na jednowymiarowej taśmie o nieograniczonej długości składającej się z ciągu kwadratów, z których każdy zawiera pojedynczy symbol z pewnego skończonego alfabetu. Alfabet składa się z rzeczywistych symboli, które same tworzą jednostki danych, oraz specjalny symbol pusty wskazujący brak informacji. Taśma zawsze będzie zawierać skończoną znaczącą porcję danych, otoczoną z każdej strony nieskończonym ciągiem symboli pustych.
Zasada 2: Upraszczanie sterowania
Jedną z najważniejszych rzeczy dla uproszczenia sterowania jest skończoność tekstu algorytmu. Procesor może znajdować się tylko w jednym ze skończonej liczby miejsc w tym tekście. Wystarczy użyć więc prymitywnego mechanizmu zawierającego pewien rodzaj układu sterowania, obejmującego skończenie wiele stanów. Stany układu będziemy traktować jako służące do kodowania miejsc w algorytmie, więc poruszanie się w nim modelujemy zmianą stanu. W każdym punkcie wykonywania algorytmu miejsce, które ma być odwiedzone jako następne, zależy od miejsca, w którym się znajdujemy, tak więc następny stan układu zależy od jego bieżącego stanu. Zmiana stanu zależy od danych oraz od bieżącego stanu. W danej chwili czasu może być czytany tylko pojedynczy symbol, więc dopuszcza się badanie tylko jednego kwadratu na raz. Mechanizm zmienia stan w zależności od wartości czytanego symbolu i swojego stanu bieżącego, przechodząc do nowego stanu. Mechanizm porusza się po taśmie przesuwając się wzdłuż po jednym kwadracie, a kierunek ruchu zależy od bieżącego stanu skrzyni biegów i bieżącego symbolu.
Opisane ograniczenia upraszczają sterowanie w algorytmie. Powstały mechanizm jest prostym mechanizmem mogącym być w jednym ze skończonej liczby stanów, poruszając się wzdłuż taśmy po jednym kwadracie. Mechanizm ten działa wyznaczając nowe stany i kierunki jako funkcje stanu bieżącego i bieżącego symbolu.
Zasada 3: Upraszczanie podstawowych operacji
Poprawność działania algorytmów zależy od poprawnego manipulowania danymi, przekształcania ich, wymazywania, czytania lub zapisywania, stosowania do nich operacji arytmetycznych lub tekstowych. Do zmiany stanu i poruszania się o jeden kwadrat w lewo lub w prawo omawiany mechanizm jest wyposażony w możliwości przekształcania w określonym stanie pewnego widzianego symbolu w jeden ze skończonej liczby dostępnych symboli.
Podstawowy model maszyny Turinga
Maszyna Turinga jest z przedstawionych modeli najprostszym modelem matematycznym komputera.
Podstawowy model przedstawiony na rysunku 2 ma skończone sterowanie, taśmę wejściową podzieloną na komórki (kwadraty) oraz głowicę taśmy, mogącą obserwować w dowolnej chwili tylko jedna komórkę taśmy. Taśma ma komórkę położoną najbardziej na lewo, ale jest prawostronnie nieskończona. Każda z komórek taśmy może zawierać dokładnie jeden symbol z skończonego alfabetu symboli. Przyjmuje się umownie, że ciąg symboli wejściowych umieszczony jest na taśmie począwszy od lewej, pozostałe komórki ( na prawo od symboli wejściowych) są wypełnione specjalnym symbolem taśmowym noszącym nazwę symbolu pustego.
Maszyna Turinga składa się z następujących elementów:
Rysunek 2. Podstawowy model maszyny Turinga
W zależności od obserwowanego symbolu przez głowicę taśmy oraz stanu sterowania skończonego, maszyna Turinga w pojedynczym ruchu:
Definicja wielotaśmowej maszyny Turinga
Struktura wielotaśmowej maszyny Turinga przedstawiona na rysunku 3. zawiera k taśm prawostronnie nieskończonych. Każda taśma podzielona jest na klatki. W każdej klatce może być umieszczony jeden symbol ze skończonego alfabetu, zwanego alfabetem symboli roboczych. Każda taśma posiada głowicę, która może poruszać się po taśmie oraz czytać lub pisać na niej symbole robocze. Operacje wielotaśmowej maszynyTuringa wyznaczone są przez pewien skończony zbiór stanów i sterowanie zawsze jest w jednym z takich stanów (stany te można traktować jako numery instrukcji w programie maszyny Turinga
Rysunek 3. Model wielotaśmowej maszyny Turinga
Formalnie maszynę Turinga (MT) nazywamy:
M = <Q,
,
, ð, q0, B, F >
gdzie:
Q - jest skończonym zbiorem stanów,
Γ - skończony zbiór dopuszczalnych symboli taśmowych,
B - symbol pusty należący do
,
Σ - podzbiór
nie zawierający B, zwany zbiorem symboli wejściowych,
ð - funkcja następnego ruchu, będąca odwzorowaniem
Q x Γ Q x Γ x { L, P } dla maszyny jednotaśmowej i
Q x Γk Q x (Γ x { L, P })k dla maszyny k - taśmowej.
gdzie:
L- oznacza ruch w lewo
P- ruch w prawo,
q0- stan początkowy,
F ⊆ Q - zbiór stanów końcowych
Działanie maszyny Turinga przedstawia się jako diagram przejść między stanami lub jako tabelę stanów, które to pojęcia zostały omówione poniżej.
Diagram przejść między stanami zawiera instrukcje, które powodują, że zmiany następują po każdym zatrzymaniu się. Diagram przejść jest grafem skierowanym, którego wierzchołki reprezentują stany. Krawędź prowadząca ze stanu s do stanu t nazywa się przejściem i etykietuje się ją kodem postaci (a/b, kierunek) gdzie a i b są symbolami,
a kierunek określa ruch głowicy w prawo bądź w lewo. Część a etykiety jest wyzwalaczem przejścia, a część <b, kierunek> akcją:
( a / | b , kierunek )
wyzwalacz | akcja
Dla układu (k+1) - elementowego, składającego się ze stanu i k symboli roboczych, funkcja przejścia określa nowy stan i k par, z których każda określa nowy symbol roboczy i kierunek ruchu głowicy. Przypuśćmy, że δ(q,a1,a2,...,ak) = (q',(a'1,d1)(a'2,d2) … (a'k,dk)) oraz maszyna Turinga jest w stanie q, a głowica taśmy o numerze i ustawiona jest nad symbolem ai, dla 1<= i<=k. Wówczas w jednym kroku maszyna Turinga przechodzi do stanu q' , zmienia symbole ai na ai' oraz przesuwa głowicę taśmy o numerze i w kierunku di, dla 1<= i<=k.
W czasie swego działania maszyna Turinga, kiedy znajdzie się w stanie s i odczytywanym symbolem będzie a to nastąpi wpisanie w to miejsce b i przesunięcie o jedno pole w kierunku kierunek. Fragment przykładowego diagramu przejść przedstawia rysunek 4.
Rysunek 3. Fragment grafu przejść między stanami dla maszyny Turinga
Aby zapobiec niejednoznaczności, co do następnego ruchu maszyny (tj. aby jej zachowanie było deterministyczne), z jednego stanu nie wychodzą dwa przejścia z tym samym wyzwalaczem. Jeden ze stanów w diagramie jest zaznaczony skierowaną do niego strzałką opatrzoną etykietą start i jest nazywany stanem początkowym. Podobnie stany z których nie wychodzą już żadne przejścia, nazywa się stanami końcowymi.
Tabela stanów - która również obrazuje przejścia między stanami maszyny Turinga zawiera wszystkie symbole
z skończonego alfabetu wejściowego jak również wszystkie stany w których może znaleźć się maszyna Turinga. Każde pole tabeli określa:
|
q0 |
q1 |
q2 |
q3 |
q4 |
|
|||||
Φ |
q1 |
q0 |
q5 |
q4 |
q5 |
|
|||||
|
B |
L |
B |
L |
C |
P |
B |
P |
C |
L |
|
A |
q0 |
q4 |
q6 |
q3 |
q7 |
|
|||||
|
Φ |
P |
C |
L |
B |
L |
A |
P |
Φ |
L |
|
B |
q1 |
q2 |
q3 |
q2 |
q3 |
|
|||||
|
A |
L |
C |
P |
D |
P |
Φ |
L |
A |
L |
|
C |
q0 |
q2 |
q0 |
q1 |
q4 |
|
|||||
|
Φ |
P |
Φ |
L |
Φ |
L |
D |
P |
D |
P |
|
Rysunek 4. Fragment stanów maszyny Turinga
Zarówno dla tabeli stanów jak i grafu przejść wyróżnia się specyficzne stany będące odpowiednio stanem początkowym i stanem (bądź stanami ) końcowym, zwane też stanami biernymi. Zakłada się, że maszyna rozpoczyna swoje działanie od swego stanu początkowego p0 na pierwszym od lewej niepustym kwadracie taśmy i postępuje krok po kroku zgodnie z narzuconym ruchem, zaś kończy działanie po osiągnięciu stanu końcowego.
Teza Churcha-Turinga
Różnorodność zadań stawianych przed maszyną Turinga postawiło pytanie :
Jakie problemy można rozwiązać odpowiednio zaprogramowaną maszyną Turinga (oczywiście pomijając czas) ?
Otóż okazuje się że:
Maszyny Turinga potrafią rozwiązać każdy efektywnie rozwiązywalny problem algorytmiczny.
Mówiąc inaczej, każdy problem algorytmiczny dla którego możemy znaleźć algorytm dający się zaprogramować w pewnym dowolnym języku, wykonujący się na pewnym dowolnym komputerze, nawet na takim, którego jeszcze nie zbudowano, ale można zbudować, i nawet na takim, który wymaga nieograniczonej ilości czasu i pamięci dla coraz większych danych, jest także rozwiązywalny przez maszynę Turinga. To stwierdzenie jest jedną z wersji tzw. tezy Churcha-Turinga (Alonz Church, Alan M. Turing), którzy doszli do niej niezależnie w połowie lat trzydziestych. Istotną sprawą jest aby uświadomić sobie, że teza Churcha-Turinga jest tezą a nie twierdzeniem, zatem nie może być dowiedziona w matematycznym tego słowa znaczeniu. Jedno z pojęć, do której się odwołuje, jest bowiem nieformalnym i nieprecyzyjnym, pojęciem “efektywnej obliczalności”.
Skąd biorą się przesłanki aby akceptować tezę Churcha-Turinga, szczególnie, jeśli nie można jej udowodnić?
Już od wczesnych lat trzydziestych badacze proponowali różne modele komputera absolutnego, wszechpotężnego, lub uniwersalnego. Chciano bowiem sprecyzować ulotne pojęcie “efektywnej obliczalności”. Na długo przedtem nim wymyślono pierwszy komputer, Turing zaproponował swoją maszynę, a Church wymyślił matematyczny formalizm funkcji zwany rachunkiem lambda (jako podstawa języka programowania Lisp). Mniej więcej w tym samym czasie Emil Post zdefiniował pewien typ systemu produkcji do manipulowania symbolami, a Stephen Kleene zdefiniował klasę obiektów zwanych funkcjami rekurencyjnymi.
Wszyscy oni próbowali użyć tych modeli do rozwiązania wielu problemów algorytmicznych, do których znane były “efektywnie wykonalne” algorytmy.
Przełomowym zdarzeniem istotnym dla wszystkich tych modeli stało się udowodnienie, iż są one równoważne w kategoriach problemów algorytmicznych, które rozwiązują. I ten fakt jest dziś nadal prawdziwy nawet dla najsilniejszych modeli, jakie można sobie wyobrazić.
Z tezy Churcha-Turinga wynika, że najpotężniejszy superkomputer z wieloma najwymyślniejszymi językami programowania, interpretatorami, kompilatorami i wszelkimi zachciankami, nie jest potężniejszy od domowego komputera z jego uproszczonym językiem programowania. Mając ograniczoną ilość czasu i pamięci mogą obydwa rozwiązać te same problemy algorytmiczne, jak również żaden z nich nie może rozwiązać problemów nierozstrzygalnych (nieobliczalnych). Schematycznie rozstrzygalność problemów przedstawia rysunek 5.
Problem algorytmiczny, do którego nie ma żadnego algorytmu jest nazywany nieobliczalnym; jeśli to problem decyzyjny nazywa się nierozstrzygalnym. Dla problemów tego typu w żaden sposób nie można skonstruować algorytmu, wykonywanego na dowolnym komputerze, bez względu na ilość wymaganego czasu i pamięci, który mógłby je rozstrzygnąć.
Rysunek 5. Sfera problemów algorytmicznych.
Najbardziej naturalnym sformułowaniem problemu, który ma być rozwiązany przez Deterministyczną Maszynę Turinga jest sformułowanie w postaci problemu decyzyjnego
Klasę P tworzą wszystkie problemy decyzyjne, które w co najwyżej w wielomianowym czasie rozwiązuje DTM.
Istnieje liczna klasa problemów, dla których nie są znane algorytmy wielomianowe, lecz dla których można w co najwyżej wielomianowym czasie zweryfikować pozytywną odpowiedź.
Dla bardziej formalnego ujęcia rozważań posłużymy się pojęciem Niedetrministycznej Maszyny Turinga (NDTM).
Przez NDTM będziemy rozumieć DTM wyposażoną dodatkowo w moduł generujący. Program NDTM jest określony w ten sam sposób co dla DTM.
Wykonanie programu przez NDTM dla łańcucha x(I), stanowiącego dane rozwiązywanego konkretnego problemu I różni się od wykonania programu przez DTM, gdyż przebiega w dwóch etapach.
Etap I: moduł generuje w całkowicie dowolny sposób i zapisuje na taśmie w komórkach -1, -2, ... , łańcuch S symboli ze zbioru Γ.
Etap 2: NDTM sprawdza, w taki sam sposób, w jaki jest wykonywany program przez DTM, czy wygenerowany łańcuch S spełnia warunki określone w pytaniu konkretnego problemu I. (Dla konkretnego problemu I może istnieć wiele takich łańcuchów S.)
ODMIANY MODELU MASZYNY TURINGA
Działanie maszyny Turinga można ograniczyć na wiele sposobów nie zmniejszając jednak klasy problemów, które rozwiązuje. Można na przykład żądać, żeby dane wejściowe pozostały nienaruszone i żeby przy zatrzymaniu taśma zawierała tylko dane i wyniki otoczone symbolami pustymi. Można zdefiniować maszynę Turinga z taśmą, która jest nieskończona tylko z prawej strony, a dane są zapisywane na taśmie od lewego skraju. Obie odmiany maszyny mogą rozwiązywać dokładnie te same problemy co model podstawowy i wobec tego nie są od niego słabsze. Podobnie dodanie maszynom dowolnie silnej własności nie powoduje żadnego rozszerzenia klasy rozwiązywalnych problemów. W żadnym z rozszerzeń nie da się rozwiązać problemu nie rozwiązywalnego.
Maszyna, która może symulować działanie dowolnej maszyny Turinga na dowolnych danych nazywa się uniwersalną maszyną Turinga. Uniwersalna maszyna Turinga U akceptuje jako dane opis dowolnej maszyny Turinga M, po którym jest umieszczony skończony ciąg X traktowany jako dane dla maszyny M. Następnie symuluje ona akcje maszyny M na taśmie, na której znajdują się dane X otoczone symbolami pustymi. Jeśli maszyna M nie może zatrzymać się na taśmie, to także nie może zatrzymać się maszyna U, jeśli maszyna M zatrzyma się to zatrzyma się również maszyna U. Obie taśmy będą wyglądać dokładnie tak samo po zakończeniu działania.
Ograniczenia narzucone na maszyny Turinga nie pomniejszają uniwersalności modelu. Oczywiście nie wszystkie ograniczenia mają tę właściwość. Maszyny, od których wymaga się, aby zatrzymywały się zaraz po uruchomieniu lub nie zatrzymywały się w ogóle , nie dokonają wiele. Istnieje również inny sposób ograniczenia modelu maszyny Turinga. Wiąże się on z ograniczeniem samego mechanizmu maszyny. Jedną z najbardziej interesujących degeneracji otrzymuje się ograniczając poruszanie się maszyny Turinga na taśmie tylko do jednego kierunku (jednokierunkowa maszyna Turinga), np. w prawo. Wynikiem jest urządzenie zwane automatem skończenie stanowym lub automatem skończonym. Automat skończony rozwiązujący problem decyzyjny działa następująco. Przechodzi wzdłuż podanej sekwencji symbol po symbolu zmieniając stan w wyniku stanu bieżącego i nowego symbolu z taśmy. Po osiągnięciu końca sekwencji zatrzymuje się, a odpowiedź zależy od tego, czy automat zatrzymał się w stanie TAK czy NIE. Automat skończony można przedstawić jako diagram przejść między stanami, tak jak dla maszyny Turinga, teraz jednak baz części <b, kierunek> w etykiecie; przejście jest etykietowane symbolem, który je wyzwala.
Maszyna Turinga może być użyta do rozpoznawania języków. Alfabet symboli roboczych maszyny zawiera również alfabet języka, zwany alfabetem symboli wejściowych. Ponadto zawiera symbol pusty B oraz być może jeszcze jakieś inne symbole robocze. Początkowo na pierwszej taśmie k-taśmowej maszyny umieszczono słowo nad alfabetem wejściowym, po jednym symbolu na klatkę, poczynając od pierwszej klatki. Wszystkie pozostałe klatki tej pierwszej taśmy zawierają symbol pusty. Pozostały taśmy maszyny Turinga są całkiem puste. Słowo wejściowe jest akceptowane przez maszynę Turinga wtedy i tylko wtedy, gdy startując od stanu początkowego i od położenia głowic wszystkich taśm na skrajnie lewej klatce, po skończonej liczbie kroków maszyna przechodzi do stanu końcowego. Język akceptowany przez maszynę Turinga jest zbiorem wszystkich słów w ten sposób akceptowanych.
Przykłady zadań rozwiązanych za pomocą maszyny Turinga
Przykład 1:
Maszyna Turinga bada problem polegający na sprawdzeniu, czy dana liczba jest parzysta
Wystarczy sprawdzić, czy w zapisie dwójkowym liczby ostatnią pozycją jest 0.
Określamy program DTM rozwiązujący ten problem przyjmując:
Γ = {0,1,b}, Σ = {0,1} , Q = {q0,q1,qn,qp} i funkcję przejść pokazaną w tabeli:
q\s |
0 |
1 |
b |
q0 |
(q0,0,P) |
(q0,1,P) |
(q1,B,L) |
q1 |
(qp,B,L) |
(qn,B,L) |
(q0,B,L) |
Przykład 2
Maszyna Turinga bada czy dane słowo jest palindromem.
Maszyna Turinga badająca czy dane słowo z alfabetu wejściowego
={a, b, c} jest palindromem (to znaczy słowem, które czyta się tak samo z obu stron). Dodatkowo przyjmuje się, że pojedynczy symbol jest palindromem. Wprowadza się dodatkowo 2 stany akceptacji SA i nieakceptacji SN. Przejście do stanu akceptacji oznacza, że dane słowo jest palindromem, zaś przejście do stanu nieakceptacji oznacza, że słowo nie jest palindromem. Tabela przejść miedzy stanami wygląda następująco:
|
q0 |
q1 |
q2 |
q3 |
q4 |
q5 |
q6 |
q7 |
q8 |
q9 |
q10 |
q11 |
Ø |
q0 |
q2 |
q10 ø, P |
q0 P |
q5 |
q10 |
q0 |
q8 |
q10 P |
q0 |
SA |
SN |
a |
q1 |
q1 P |
q3 |
q3 L |
q4 P |
q11 P |
q6 |
q7 P |
q11 P |
q9 |
S.A. |
SN |
b |
q4 P |
q1 P |
q11 P |
q3 |
q4 |
q6 |
q6 |
q7 |
q11 P |
q9 |
S.A. |
SN |
c |
q7 P |
q1 P |
q11 P |
q3 L |
q4 P |
q11 P |
q6 |
q7 P |
q9 |
q9 |
S.A. |
SN |
Tabela stanów
q1 - pamięta odczytaną literę a |
q2 - i natrafia ø |
q3 - i cofa się do początku |
q4 - pamięta odczytaną literę b |
q5 - i natrafia ø |
q6 - i cofa się do początku |
q7 - pamięta odczytaną literę c |
q8 - i natrafia ø |
q9 - i cofa się do początku |
q10 - |
Symulacja akcji maszyny Turinga dla taśmy zawierającej słowo abba
Głowica maszyny umieszczona jest na kwadracie zawierającym a znajdujące się najbardziej na lewo. Maszyna "pamięta" pierwszy przeczytany symbol, po czym wymazuje go zastępując symbolem pustym i przechodzi w prawo, aż do osiągnięcia pierwszego symbolu pustego. (etap 1-5)
Maszyna przesuwa się o jeden symbol w lewo, zatrzymuje się więc na najbardziej prawym symbolu (etap 6), w omawianym przypadku jest to symbol a. Gdyby odczytany symbol był różny od zapamiętanego, to maszyna przeszłaby do stanu nieakceptacji.
Maszyna wymazuje odczytany najbardziej prawy symbol a i przechodzi do stanu, który doprowadza ją do pierwszego symbolu pustego po lewej stronie słowa. (etap 10)
Maszyna przesuwa się o jeden kwadrat w prawo i zapamiętuje przeczytany symbol, drugi symbol słowa - symbol b. Ruszając się w prawo maszyna porówna zapamiętany symbol z przedostatnim symbolem słowa. (etap 13)Porównanie kończy się sukcesem i maszyna wymazuje symbol b.
Maszyna rusza w lewo w poszukiwaniu dalszych symboli. Nie znajdując żadnego i nie osiągając stanu nieakceptacji przechodzi do stanu akceptacji. (etap 14-16)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rysunek 6. Symulacja akcji maszyny Turinga dla taśmy zawierającej słowo abba.
Języki formalne, gramatyki, odwrotna notacja polska
Języki i gramatyki formalne
alfabet - dowolny zbiór symboli, z których będą zestawiane słowa języka,
słowo - uporządkowany ciąg symboli alfabetu,
język - zbiór wszystkich możliwych słów,
gramatyka - zbiór reguł umożliwiających generowanie słów danego języka jak też rozróżnienie słów poprawnie zbudowanych od niepoprawnie zbudowanych.
Przykład
Alfabet - {a, b}
Słowo - np. aaaab, bbbb, a , b
Gramatyka - Reguła 1: a jest poprawne (tzn. słowo zbudowane z pojedynczego symbolu a jest poprawne).
Reguła 2: jeżeli α jest poprawne , to aαb też jest poprawne.
Przykłady pojedynczych słów:
a - na podstawie Reguły 1.
aab - na podstawie Reguły 1 i Reguły 2.
aaabb - na podstawie Reguły 1 i dwukrotnie stosowanej Reguły 2.
Gramatyką nazywamy czwórkę
G = ( V, Σ , P , δ )
gdzie:
V - zbiór symboli terminalnych (alfabet końcowy),
Σ - zbiór symboli nieterminalnych (alfabet pomocniczy),
P - lista produkcji,
δ - słowa języka.
Słownikiem A nazywamy zbiór będący sumą mnogościową alfabetu końcowego i alfabetu pomocniczego: A = V ∪ Σ.
Przez A* oznaczamy zbiór wszystkich skończonych ciągów (napisów), których elementy należą do zbioru A.
Język L(G) to zbiór wszystkich słów poprawnych w sensie gramatyki G, tzn. wyprowadzalnych z δ przez listę produkcji P.
Symbol ε oznacza ciąg pusty.
Klasyfikacja gramatyk według Chomskiego:
Wszystkie gramatyki mają postać
u w
gdzie:
u ∈ A* - { ε }
w ∈ A*
Wszystkie produkcje mają postać:
uXw ubw
gdzie:
u, w ∈ A*
X ∈ Σ
b ∈ A* - {ε}
Wszystkie produkcje mają postać:
X b,
gdzie :
X ∈ Σ
b ∈ A* - {ε}
Wszystkie produkcje mają postać:
X bY (gramatyki prawostronnie regularne)
X Yb (gramatyki lewostronnie regularne)
gdzie :
X ∈ Σ
Y ∈ Σ ∪ {ε}
b ∈ A* - {ε}
Można łatwo się przekonać, że każda gramatyka klasy „i” jest jednocześnie gramatyką klasy „j”, gdzie 0 <= j <= i
Przykład 1.
Definiowanie gramatyki generującej wyrażenia postaci:
anbmck; n, m, k ∈N,
gdzie:
df
ai = a a ... a
i razy
Rozwiązanie:
Należy zdefiniować kolejno:
V, Σ , P , δ
Zatem otrzymujemy:
V = {a, b, c}
Σ = {W, Z, U}
P: <W>::=a<W>a<Z>
<Z>::=b<Z>b<U>
<U>::=c<U>c
δ = W
Przykład 2.
Zdefiniować gramatykę generującą wyrażenia postaci:
anbkcn
gdzie:
df
ai = a a ... a
i razy
Rozwiązanie:
V = {a, b, c}
Σ = {W, U}
P: <W>::=a<W>ca<U>c
<U>::=b<U>b
δ = W
Przykład 3,
Zdefiniować gramatykę generującą liczby całkowite. Liczba składa się z niepustego ciągu cyfr i może zawierać znak.
Rozwiązanie:
V = {0,1,2,3,4,5,6,7,8,9,+,-}
Σ = {LC,L,C,Z}
P:<LC>::=<Z><L> <L>
<L> ::=<C><L> <C>
<C> ::= 0 1 2 3 4 5 6 7 8 9
<Z> ::= + -
δ = LC
Przykład 4.
Dany jest język L(G):
G = <V,Σ,P,δ>
V = {a,b, … ,z,+,(,),*}
Σ = {W,S,C}
P = <W> ::= <W>+<S>| <S>
<S> ::= <S>*<C>|<C>
<C> ::= (<W>) a|b|c| ... |z
δ = W
Czy słowo:
(((a+b * d) * d+a))* a+b+d
jest słowem poprawnym języka L(G) ?
Rozwiązanie:
.....................
{ przedstawiono na wykładzie }
Beznawiasowe algebry Łukasiewicza
Notacje umożliwiająca zapisanie dowolnego wyrażenia arytmetycznego bez użycia nawiasów zmieniających kolejność wykonywania działań.
Odwrotna Notacja Polska (ang. reverse Polish notation)
system notacji beznawiasowej umożliwiający zapisywanie wyrażeń w ten sposób, że argumenty operacji poprzedzają operatory (notacja przyrostkowa)
Ze względu na łatwość obliczania wyrażeń zapisanych w ONP przy użyciu stosu znalazła ona szerokie zastosowanie w arytmetyce komputerów.
Gramatyka pozwalająca na generowanie napisów w ONP oraz Algorytm dokonujący zamiany wyrażeń zapisanych w arytmetyce nawiasowej na ONP.
V = {a,b,d,+,*}
P: <W> ::= <Z><Z><O>|<Z>
<Z> ::= <X><X><O>|<X>
<X> ::= a | b | d
<O> ::= +|*
Przykłady prostych wyrażeń arytmetycznych i odpowiadający im zapis w ONP:
1)
(a+b)*d a b + d *
2)
(a + b)/c*(d-e) ab+c/de-*
Oprócz Odwrotnej Notacji Polskiej istnieje także Notacja Polska. Zmiana dotyczy produkcji:
P: <W> ::= <O><Z><Z>|<Z>
<Z> ::= <O><X><X>|<X>
<X> ::= a | b | d
<O> ::= +|*
Algorytm wyznaczania wartości wyrażenia w ONP
T
N
N T
N T
Przykład
Obliczyć wartość wyrażenia: 2 3 4 5 + * +
Definicja
Translacja to przekład tekstów zredagowanych w jednym języku źródłowym na równoważny semantycznie tekst w innym języku - wynikowym.
Translacja prostych wyrażeń arytmetycznych na zapis w odwrotnej notacji polskiej (ONP) wymaga ustalenia tablicy priorytetów dla operatorów arytmetycznych.
Tablica priorytetów:
Operator |
Priorytet |
Funkcja (lg, sin, exp, ...) |
0 |
Potęgowanie ( ↑ ) |
1 |
Mnożenie, dzielenie, negacja ( *, / , ) |
2 |
Dodawanie, odejmowanie (+, -) |
3 |
Wzrost
Priorytetu
Reguły translacji przy użyciu stosu:
Konwencja graficzna:
WEJŚCIE |
|
STOS |
|
WYJŚCIE STOSU |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SZCZYT STOSU |
|
|
błąd
KONIEC
φ
operator
pobierz argumenty ze stosu, wykonaj działanie, wynik na stos
stos
argument
pobierz symbol z lewej ku prawej
start
Wyszukiwarka
Podobne podstrony:
quota, !!!Uczelnia, wsti, materialy, II SEM, systemy operacyjne linux
Analiza i przetwarzanie obraz w W.1, !!!Uczelnia, wsti, materialy, III SEM, Wyk ady
Statystyki, !!!Uczelnia, !WSTI
nowe zadanie, !!!Uczelnia, wsti, materialy, III SEM, teleinformatyka, zadania raporty
algorytmy egzamin, !!!Uczelnia, wsti, materialy, II SEM, algorytmy struktury danych
algebra zbior w, !!!Uczelnia, wsti, materialy, II SEM, matematyka
ALGORYTMY I STRUKTURY DANYCH, !!!Uczelnia, wsti, materialy, II SEM, algorytmy struktury danych
Etyka hackera, !!!Uczelnia, !WSTI
WIRTUALNA SIE PRYWATNA, !!!Uczelnia, wsti, materialy, III SEM, teleinformatyka, voip vpn
Serwer Poczty, !!!Uczelnia, wsti, materialy, III SEM, teleinformatyka, windows2003 server
Aspekt prawny, !!!Uczelnia, !WSTI
AiSD Egzamin 2005, !!!Uczelnia, wsti, materialy, II SEM, algorytmy struktury danych
lista pytan ustne, !!!Uczelnia, wsti, materialy, III SEM, programowanie c
Social Engineering, !!!Uczelnia, !WSTI
zadanie1 tresc, !!!Uczelnia, wsti, materialy, III SEM, teleinformatyka
AiSD Egzamin Zadania, !!!Uczelnia, wsti, materialy, II SEM, algorytmy struktury danych
Adresacja fizyczna i logiczna IP i MAC, !!!Uczelnia, wsti, materialy, I SEM, uzytkowanie sieci
Analiza i przetwarzanie obraz w W.6, !!!Uczelnia, wsti, materialy, III SEM, Wyk ady
Analiza i przetwarzanie obraz w W.7, !!!Uczelnia, wsti, materialy, III SEM, Wyk ady
więcej podobnych podstron