WYDZIAŁ ELEKTRONKI TELEKOMUNIKACJI I INFORMATYKI KATEDRA METROLOGII I SYSTEMÓW ELEKTRONICZNYCH LABORATORIUM METROLOGII I TECHNIKI EKSPERYMENTU GRUPA 4A
Ćwiczenie nr 6 Pomiary elementów RLC	Imię i nazwisko	Dariusz Kos
		Data wykonania ćwiczenia	24.05.2005
		Data odbioru sprawozdania	01.06.2005
		Ocena zaliczenia
		Uwagi i podpis

Sprawozdanie

12.5.1. Pomiary rezystancji mostkiem Wheatstone'a

Tablica 12.1

R1 [Ω]	ΔRx [Ω]	ΔU [mV]	SU [ mV/Ω]
10	207.6	10.00	0.05
100	20.9	10.00	0.48
1 000	7.4	10.02	1.35
10 000	22.2	10.45	0.47

Tablica 12.2

R2 [Ω]	ΔRx [Ω]	ΔU [mV]	SU [ mV/Ω]
10	10.1	10.00	0.99
100	8.1	9.98	1.23
1 000	6.8	10.02	1.47
10 000	6.8	10.05	1.48

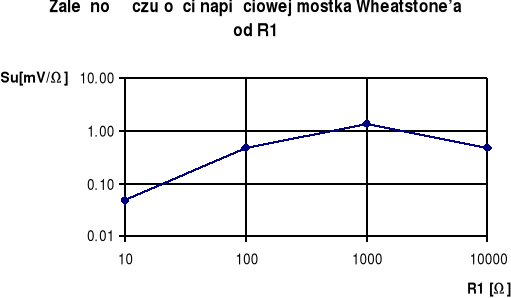
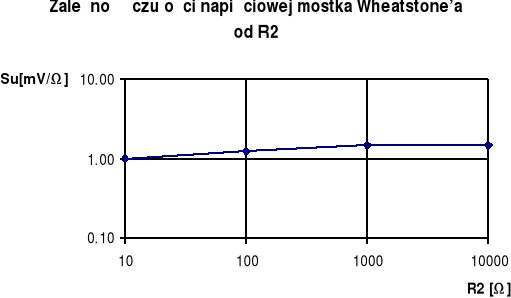
R_{1 max czułości} = 1000Ω

Wniosek:

Dla uzyskania optymalnych warunków pomiaru należy dobrać rezystor R₁ tak, by jego rezystancja była zbliżona do rezystancji badanego rezystora. Rezystor R₂ nie ma większego wpływu na dokładność pomiaru, choć najlepszą czułość uzyskałem, gdy jego rezystancja była większa lub równa rezystancji R₁.

12.5.2. Pomiary małej rezystancji mostkiem Thomsona

R_N = 0.1Ω

R = 10000Ω

R_p = 3141.1Ω

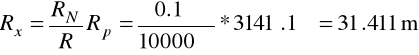
W celu obliczenia grubości ścieżki obwodu drukowanego, znając jej rezystancję, posługujemy się wzorem na opór przewodnika:

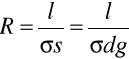
R - opór przewodnika; R = R_x = 31.411mΩ

l - długość przewodnika; l = 0.05m

σ - przewodność właściwa; σ = 56m/Ωmm²

s - pole przekroju przewodnika; s = d * g, gdzie:

d - szerokość przewodnika; d = 2mm

g - grubość przewodnika

Po przekształceniu powyższego wzoru otrzymujemy:

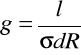
12.5.3. Porównanie pomiarów małej rezystancji.

Wykonaliśmy szereg pomiarów rezystancji ścieżki obwodu drukowanego różnymi metodami:

Metoda mostka Thomsona:	RTh = 31.411mΩ
Metoda dwuprzewodowa:	R2W = 46mΩ
Metoda czteroprzewodowa:	R4W = 28mΩ
Metoda techniczna:	RTech = 33.5948mΩ

Wniosek:

Można przyjąć, że metoda czteroprzewodowa wykonana multimetrem cyfrowym 34401A jest najdokładniejsza, gdyż wnosiła najmniejszą rezystancję połączeń do rezystancji mierzonej. Okazuje się natomiast, że metoda dwuprzewodowa wprowadza największy błąd pomiaru i praktycznie nie nadaje się do dokładnych pomiarów małych rezystancji. Bardziej skomplikowane metody jak metoda mostka Thomsona czy metoda techniczna dały już wyniki bardziej zbliżone do wyników metody czteroprzewodowej.

12.5.4. Pomiar rezystancji rezystora wzorcowego.

R_N = 0.1Ω

R_2W = 0.107Ω

R_4W = 0.101Ω

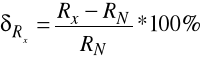
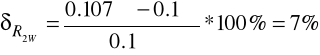
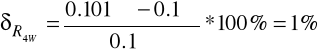
12.5.5. Pomiar rezystancji elementu nieliniowego metodą techniczną

Tablica 12.4

IDC [mA]	2	4	8	12	16	20
UDC [V]	0.40337	1.3173	4.0957	7.9754	11.687	16.409
R [Ω]	0.20169	0.3293	0.5120	0.6646	0.730	0.820

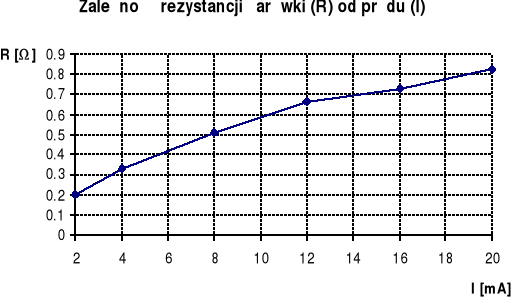
12.5.6. Pomiar kondensatora o dużym współczynniku stratności D miernikiem HM 8018

C₀ = 168.1nF

Tablica 12.5

Rd [kΩ]	100	10	5	2	1	0.6
Cx [nF]	168.0	167.9	168.0	168.1	168.3	167.9
Gx [μS]	14	105	206	506	1009	1677
Dp	0.0083	0.0625	0.1225	0.3010	0.6002	0.9976
δCx [%]	-0.06	-0.12	-0.06	0.00	0.12	-0.12

Tablica 12.6

Rd [Ω]	0	100	200	300	500	700
Cx [nF]	167.9	163.0	150.4	133.3	98.0	70.0
Rx [Ω]	0	100	201	301	501	701
Ds	0	0.1681	0.337881	0.505981	0.842181	1.178381
δCx [%]	-0.12	-3.03	-10.53	-20.70	-41.70	-58.36

(pulsacja sygnału pomiarowego ω=10000 rad/s)

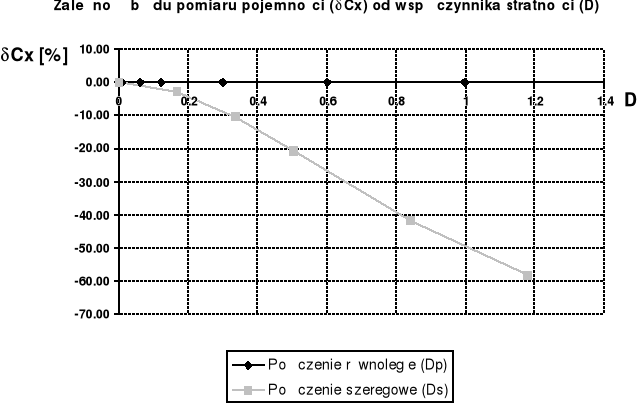
Wniosek:

W konfiguracji szeregowej wystąpiły znaczne błędy pomiaru pojemności. Jest to spowodowane faktem, że miernik HM 8018 został skonstruowany do mierzenia pojemności w konfiguracji równoległej.

12.5.7. Pomiar kondensatorów o małych wartościach pojemności

Obserwacje:

Przy połączeniu kondensatora do miernika zwykłymi przewodami, występowały duże wahania pomiaru, szczególnie przy zbliżaniu do siebie przewodów, zbliżania lub owijania ich wokół ręki.

Dołączenie kondensatora przewodami ekranowanymi ale nieuziemionymi zmniejszyło wahania, natomiast pomiar wciąż był niedokładny.

Dołączenie ekranu do masy miernika spowodowało całkowity zanik wahań i poprawienie dokładności pomiaru.

Wnioski:

Zwykłe przewody stanowią swoisty kondensator, stąd zbliżanie ich do siebie powodowało zmianę ich pojemności i duży wpływ na pomiar. Podobny efekt dotyczy przewodów ekranowanych niedołączonych do masy, gdyż do pojemności wzniesiona zostaje pojemność ekranu. Dopiero podłączenie masy eliminuje ten wpływ.

Ćwiczenie to pokazuje, że ważne bardzo istotne jest zapewnienie odpowiedniego środowiska przy pomiarze małych pojemności.

12.5.8. Pomiar indukcyjności i rezystancji miernikiem LC

L_x = 39.3mH, R_x = 15Ω, ω = 10000rad/s

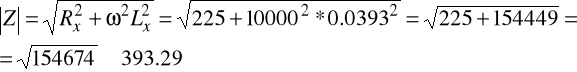
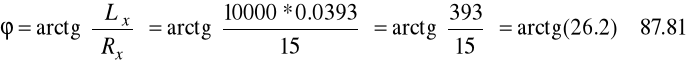
12.5.9. Pomiar cewek o małych wartościach indukcyjności

L_N = 10μH

L_x2 = 10.8μH R_x2 = 1.19Ω.

L_x4 = 9.0μH R_x4 = 0.93Ω.

Wniosek:

W pomiarze metodą dwuzaciskową wpływ ma rezystancja doprowadzeń, stąd R_x2 > R_x4, natomiast nieoczekiwanie wartość zmierzonej indukcyjności jest bardziej zbliżona do nominalnej niż w przypadku metody czterozaciskowej.

12.5.10. Pomiar pojemności kondensatora multimetrem cyfrowym Metex M-4650CR

C₀ = 178.45nF

Tablica 12.7

Rd [kΩ]	50	20	10	7	5	4
Cx [nF]	178.35	179.05	182.20	186.91	195.71	191.00
δCx [%]	-0.06	0.34	2.10	4.74	9.67	7.03

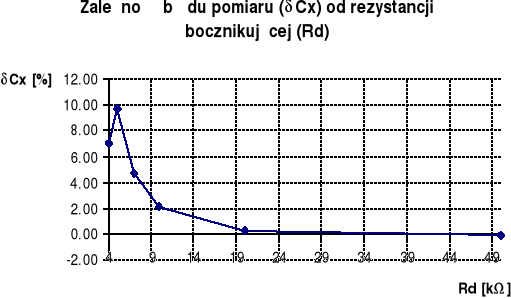
Wnioski:

Miernik M-4650CR nie jest przystosowany do pomiarów pojemności w konfiguracji równoległej, ponieważ im mniejsza rezystancja rezystora bocznikującego tym większy prąd ładujący będzie spływał przez bocznik zamiast przez kondensator.

Metoda zastosowana w tym mierniku sprawdzi się natomiast w konfiguracji szeregowej, z którą to nie radził sobie miernik HM 8018.

Oba mierniki uzupełniają się wzajemnie, dzięki czemu możemy wykonywać dokładne pomiary zarówno w konfiguracji równoległej jak i w szeregowej.

Strona 1/2

Strona 5/2

---