1. wwDefinicje wielkości mierzonych

Długość fali (λ) jest to najmniejsza odległość pomiędzy dwoma punktami o tej samej fazie drgań. Dla fali sinusoidalnej najłatwiej określić jej długość wyznaczając odległość między dwoma sąsiednimi grzbietami.

Stała siatki dyfrakcyjnej to parametr charakteryzujący siatkę dyfrakcyjną. Wyraża on rozstaw siatki tj. odległość między środkami kolejnych szczelin.

2. Wyznaczanie długości fali przy pomocy suwmiarki

2.1. Schemat układu pomiarowego - suwmiarka

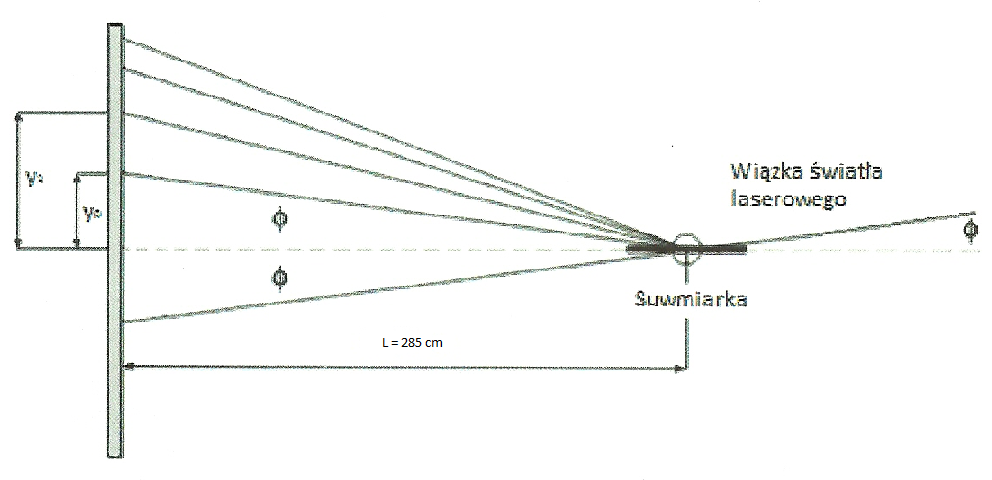
Schemat 1: Światło laserowe - suwmiarka

2.2 Tabelaryczne zestawienie wyników pomiaru

n	y[m]	Y [m]	Δy[m]	ΔY [m]
1	0,064	0.004096	0,0075	0.00096
2	0,104	0.010816	0,003	0.000624
3	0,132	0.017424	0,0025	0.00066
4	0,155	0.024025	0,0025	0.000775
5	0,174	0.030276	0,002	0.000696
6	0,193	0.037249	0,002	0.000772
7	0,209	0.043681	0,0015	0.000627
8	0,224	0.050176	0,0015	0.000672
9	0,238	0.056644	0,0015	0.000714
10	0,252	0.063504	0,0015	0.000756
11	0,264	0.069696	0,0015	0.000792
12	0,277	0.076729	0,0015	0.000831
13	0,288	0.082944	0,0015	0.000864
14	0,299	0.089401	0,0015	0.000897
15	0,309	0.095481	0,0015	0.000927
16	0,32	0.1024	0,001	0.00064

Tabela 1

Legenda do tabeli 1:

n - numer plamki yn - odległość kolejnych plamek od punktu 0 Y - podniesiona wartość yn do kwadratu u(y) - niepewność pomiarowa yn plamki ΔY - niepewność pomiaru dla Y

2.3. Obliczenia

Niepewności pomiarowe wyliczono ze wzoru:

ΔY =

Gdzie:

u(y_n) - niepewność pomiarowa y_n plamki

A zatem przykładowe obliczenia niepewności pomiarowych wyglądają następująco:

ΔY =

2*0,064*0,0070=0,001792

2.4.Wykres zależności y_n² dla n= 1, 2, 3, ...

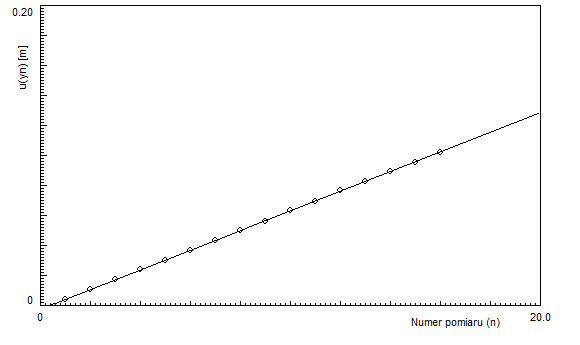
Y=An+B

2.5. Aproksymacja wyników pomiarów

Aproksymację wyników przeprowadzono w programie „Matex” z zależności liniowej :

Gdzie:

W wyniku tego otrzymaliśmy następujące wartości:

Chi²=9,49*10^-1

Ndf=14

Parametr (A±u(A))= 6,55*10^-3±0,41·10^-4

Parametr (B±u(B))= -2,22*10^-2±0, 38·10^-3

Dla zbadania prawidłowości hipotezy wykorzystaliśmy wzór:

Ponieważ iloraz chi² przez ndf jest równy 0,351 czyli jest mniejszy od 1, hipotezę uznaliśmy za poprawną

2.6. Obliczanie długości fali

Do obliczania długości fali wykorzystaliśmy wzór:

Gdzie:

1. parametr A wyznaczony za pomocą programu „Matex”(6,5451*10^-3)

λ- długość fali

L- odległość suwmiarki od ekranu (2,71 m)

d- odległość między środkami poszczególnych podziałek na suwmiarce (0,001m)

Po przekształceniu wzoru otrzymaliśmy:

Podstawiając odpowiednie wartości obliczamy długość fali:

[m]

Następnie obliczyliśmy złożoną niepewność standardową dla długości fali:

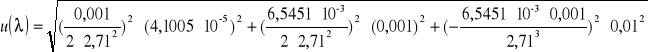
u(λ)= 4,54275*10^-7

Wynik ostateczny: λ + u(λ)=(
±454,28*10^-9) [m]

2.7.Porównanie wyniku z wartością tablicową

Z informacji odczytanych z lasera wynika, że długość fali powinna zawierać się w przedziale 630 - 680 nm. Otrzymany przez nas wynik różni się od wartości odczytanej i wynosi: 582nm. Spowodowane to mogło być małą dokładnością używanych przyrządów pomiarowych czy niewystarczającą precyzją ludzkiego oka. Na uzyskany przez nas wynik ma wpływ niepewność pomiarowa typu A.

3.Wyznaczanie stałej siatki dyfrakcyjnej

3.1. Schemat układu pomiarowego - siatka dyfrakcyjna

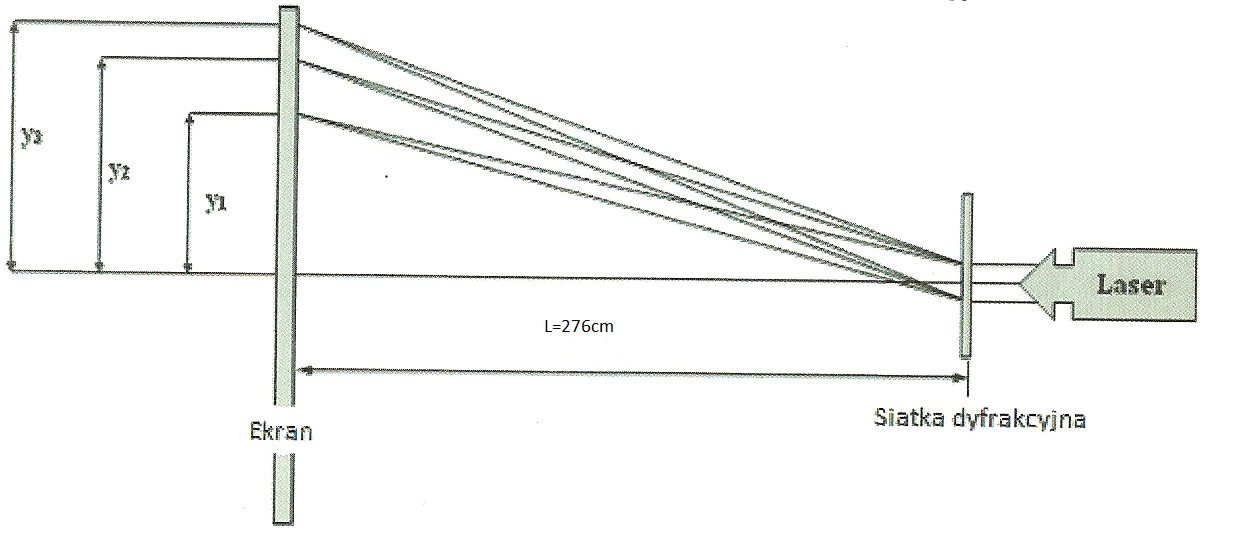
Schemat 2: Światło laserowe - siatka dyfrakcyjna

3.2. Tabelaryczne zestawienie wyników pomiaru

n	yn [m]	ΔY [m]
1	0,34	0,002
2	0,71	0,002
3	1,12	0,002

Tabela 2

Legenda do tabeli 2:

n- numer plamki yn- odległość kolejnych plamek od punktu 0 ΔY- dokładność przyrządu pomiarowego

3.3. Obliczenia - stała siatki dyfrakcyjnej

Do obliczenia stałej siatki dyfrakcyjnej wykorzystaliśmy wzór:

Gdzie:

D- stała siatki dyfrakcyjnej

n- numer plamki

- długość fali

Podstawiając za:

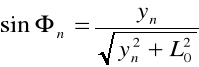
Otrzymaliśmy:

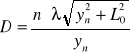
Przykładowe obliczenia dla plamki nr 1 wyglądają następująco:

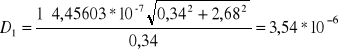
[m]

Wyniki pozostałych obliczeń przedstawiono w tabeli 3:

n	yn [m]	Dn [m]
1	0,34	3,54055*10^-^6
2	0,71	3,48004*10^-^6
3	1,12	3,46689*10^-^6

Legenda do tabeli 3:

n- numer plamki yn- odległość kolejnych plamek od punktu 0 D- stała siatki dyfrakcyjnej

W celu wyznaczenia stałej siatki dyfrakcyjnej uśredniono otrzymane wyniki, korzystając ze wzoru:

)+(
)+(
)]

D=3,5*10^-6

Następnie obliczyliśmy niepewności standardowe typu A dla stałej siatki dyfrakcyjnej:

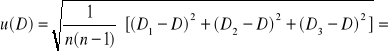
u(D)= 3,77*10^-8

Wynik ostateczny: D±u(D)= 3,5*10^-6±3,77*10^-8[m]

3. Wnioski

Wykonując ćwiczenie poznaliśmy metodę wyznaczania długości fal ugiętego światła laserowego. Wykorzystując zjawisko dyfrakcji oraz interferencji zapoznaliśmy się z metodą wyznaczania stałej siatki dyfrakcyjnej.

Po obliczeniach wyznaczyliśmy długość fali, która w naszym przypadku wynosi 446nm. Wynik ten różni się od wartości odczytanej wynoszącej ( 630-680 nm). Nie wątpliwie jest to spowodowane:

- niedokładnością pobranych pomiarów

- małą dokładnością używanych przyrządów pomiarowych

- doświadczeniem studentów w podobnych pomiarach

Ponad to papierowy pasek (służący do nanoszenia punktów wyświetlanych na ekranie) podczas pomiaru mógł ulec przemieszczeniu.

Uzyskany przez nas wynik obarczony jest niepewnością pomiarową typu A.

Wartości uzyskane dla stałej siatki dyfrakcyjnej nieznacznie się od siebie różniły, więc wyniki te uśredniliśmy i obliczyliśmy niepewność standardową typu A.

---