Przykład

Analiza możliwości zaopatrzenia w wodę zakładu przemysłowego

Bezpośrednio poniżej przekroju wodowskazowego A projektowana jest budowa zakładu przemysłowego, którego potrzeby wodne są stałe w czasie i wynoszą 2.4 m³/s. Należy zbadać możliwości zaopatrzenia w wodę zakładu przemysłowego z zasobów rzeki w oparciu o następujące dane:

1) n-letni ciąg przepływów średnich okresowych

(Q_ij [m³/s]; i=1,2,...,n; j=1,2,...,m)

gdzie:

n - liczba lat;

m - ilość okresów, na jakie podzielono rok,

w rozpatrywanym przykładzie n = 1 rok, m = 12 miesięcy;

Dane o przepływach średnich miesięcznych zestawiono w tabeli 1.

2) wielkość przepływu nienaruszalnego QN [m³/s] na odcinku rzeki poniżej ujęcia dla zakładu przemysłowego, (QN = 0.50 m³/s);

3) wymagana przez zakład przemysłowy gwarancja czasowa G_kr [-] zaspokojenia potrzeb wodnych, (G_kr = 0.80);

Rys. 1. Schemat lokalizacyjny elementów systemu wodnego

Oznaczenia i definicje

Długość przedziału czasowego (Δt_ij)

Dyspozycyjne zasoby wodne (QD_ij)

Pobór wody przez użytkownika (X_ij)

Deficyt wody u użytkownika (D_ij)

Gwarancja czasowa (G_t) zaspokojenia potrzeb wodnych użytkownika

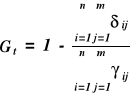
gdzie:

Gwarancja objętościowa (G_v) zaspokojenia potrzeb wodnych użytkownika

Tabela 1. Analiza możliwości zaopatrzenia w wodę zakładu przemysłowego z zasobów rzeki

Rok	Miesiąc	Δtij	Qij	QDij	QDij Δtij	Pij	Pij Δtij	Xij	Xij Δtij	Dij	Dij Δtij	δij
i	j	[mln s]	[m^3/s]	[m^3/s]	[mln m^3]	[m^3/s]	[mln m^3]	[m^3/s]	[mln m^3]	[m^3/s]	[mln m^3]
1	1	2.678	2.7	2.2	5.89	2.4	6.43	2.2	5.89	0.2	0.54	1
1	2	2.419	3.2	2.7	6.53	2.4	5.81	2.4	5.81	0	0.00	0
1	3	2.678	3.3	2.8	7.50	2.4	6.43	2.4	6.43	0	0.00	0
1	4	2.592	2.8	2.3	5.96	2.4	6.22	2.3	5.96	0.1	0.26	1
1	5	2.678	2.4	1.9	5.09	2.4	6.43	1.9	5.09	0.5	1.34	1
1	6	2.592	3.1	2.6	6.74	2.4	6.22	2.4	6.22	0	0.00	0
1	7	2.678	3.5	3.0	8.03	2.4	6.43	2.4	6.43	0	0.00	0
1	8	2.678	2.5	2.0	5.36	2.4	6.43	2.0	5.36	0.4	1.07	1
1	9	2.592	2.8	2.3	5.96	2.4	6.22	2.3	5.96	0.1	0.26	1
1	10	2.678	3.6	3.1	8.30	2.4	6.43	2.4	6.43	0	0.00	0
1	11	2.592	2.7	2.2	5.70	2.4	6.22	2.2	5.70	0.2	0.52	1
1	12	2.678	2.4	1.9	5.09	2.4	6.43	1.9	5.09	0.5	1.34	1
Suma		31.5	35.0	29.0	76.15	28.8	75.68	26.8	70.36	2.0	5.33	7
Średnia		2.63	2.92	2.42	-	2.4	-	2.23	-	0.17	-	-
								Gwarancja czasowa Gt=				0.42
								Gwarancja objętościowa Gt=				0.93

Rys. 2. Analiza porównawcza zasobów dyspozycyjnych i potrzeb wodnych

Rys. 3 Wykres deficytów wody

Gwarancja czasowa spełnienia potrzeb wodnych użytkownika G_t = 0.42.

Pojawił się problem: „Dyspozycyjne zasoby wodne rzeki nie wystarczają na pokrycie potrzeb zgłaszanych przez użytkownika z wymaganą gwarancją G_kr = 0.80”.

Co można zrobić w takiej sytuacji?

1. Zwiększenie dyspozycyjnych zasobów wodnych poprzez budowę zbiornika retencyjnego powyżej ujęcia wody dla zakładu przemysłowego;

2. Zwiększenie dyspozycyjnych zasobów wodnych poprzez budowę kanału przerzutowego z innej zlewni, zasilającego rzekę powyżej ujęcia dla zakładu przemysłowego;

3. Zwiększenie dyspozycyjnych zasobów wodnych poprzez budowę ujęcia wód podziemnych;

4. Ograniczenie potrzeb wodnych zakładu przemysłowego poprzez zmianę technologii produkcji.

Dokonanie świadomego i racjonalnego wyboru jednego z wymienionych wyżej rozwiązań wariantowych (lub wariantu będącego ich kombinacją) wymaga wykonania dodatkowych obliczeń symulacyjnych, mających na celu określenie parametrów obiektów hydrotechnicznych w poszczególnych wariantach (pojemność użytkowa zbiornika retencyjnego, przepustowość kanału przerzutowego, wydajność ujęcia wód podziemnych) oraz wymaganego stopnia redukcji zapotrzebowania na wodę.

Wyznaczenie pojemności użytkowej zbiornika retencyjnego

Rozwiązanie problemu polega na wyznaczeniu możliwie najmniejszej pojemności użytkowej zbiornika, która umożliwi dostarczenie do zakładu przemysłowego odpowiedniej ilości wody z wymaganą gwarancją.

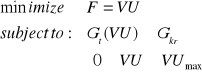
gdzie:

G_t (VU) - funkcja kryterialna określająca wielkość gwarancji zaspokojenia potrzeb wodnych zakładu przemysłowego w zależności od pojemności użytkowej zbiornika retencyjnego,

VU_max - oznacza maksymalną możliwą do wybudowania, ze względu na warunki terenowe, pojemność użytkową zbiornika.

Rys. 4. Schemat procedury wyznaczania pojemności użytkowej zbiornika retencyjnego (ε_VU - wymagana dokładność określenia VU)

Plan dyspozytorski

Polityka standardowa

Zgodnie z zasadami polityki standardowej odpływ (T) ze zbiornika dla rozpatrywanego okresu oblicza się z następującej zależności:

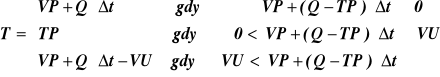
gdzie: VU - pojemność użytkowa zbiornika retencyjnego [mln m³],

VP - napełnienie zbiornika na początku danego okresu [mln m³],

Q - dopływ wody do zbiornika w danym okresie [m³/s]

TP - pożądany odpływ ze zbiornika w danym okresie [m³/s],

Δt - długość przedziału czasowego [mln s],

T - odpływ ze zbiornika w danym okresie [m³/s].

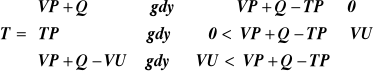
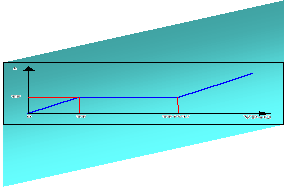
Rys. 5. Polityka standardowa

W rozpatrywanym przykładzie przyjęto:

VU ∈ <VU_min=0; VU_max=2.5 mln m³>

Należy wyznaczyć możliwie najmniejszą pojemność użytkową zbiornika (z dokładnością ε_VU=0.1 mln m³), która umożliwi zaspokojenie potrzeb wodnych zakładu przemysłowego z gwarancją nie mniejszą niż G_kr=0.80.

Przyjęto, że na początku pierwszego roku pojemność użytkowa zbiornika jest całkowicie wypełniona wodą (napełnienie początkowe VP_1,1=VU).

W rozpatrywanym przykładzie odpływ pożądany TP jest równy sumie przepływu nienaruszalnego i potrzeb wodnych zakładu przemysłowego:

W pierwszym kroku przyjęto, że obliczeniowa pojemność użytkowa wynosi:

Dla pierwszego miesiąca zasoby dyspozycyjne wynoszą:

Wielkość zasobów dyspozycyjnych (VP+Q = 8.48) jest większa od odpływu pożądanego (TP = 7.77) przyjmujemy odpływ równy TP.

Wypuszczamy odpływ T równy odpływowi pożądanemu, a resztę wody magazynujemy w zbiorniku, tzn. napełnienie końcowe zbiornika wyniesie:

Napełnienie końcowe w danym okresie staje się napełnieniem początkowym (VP) dla okresu następnego.

Zrzutem jałowym nazywa się ilość wody, która odpływa bezproduktywnie z systemu wodnego - nie jest potrzebna użytkownikom i nie może być zmagazynowana w zbiorniku.

Tabela 2. Symulacja pracy zbiornika retencyjnego

						VU=	1.25
Miesiąc	Q	VP	TP=P+QN	Zdys=Q+VP	T	VK	ZJ
	[mln m^3]	[mln m^3]	[mln m^3]	[mln m^3]	[mln m^3]	[mln m^3]	[mln m^3]
1	2	3	4	5	6	7	8
1	7.23	1.25	7.77	8.48	7.77	0.71	0.00
2	7.74	0.71	7.02	8.46	7.21	1.25	0.19
3	8.84	1.25	7.77	10.09	8.84	1.25	1.07
4	7.26	1.25	7.52	8.51	7.52	0.99	0.00
5	6.43	0.99	7.77	7.42	7.42	0.00	0.00
6	8.04	0.00	7.52	8.04	7.52	0.52	0.00
7	9.37	0.52	7.77	9.89	8.64	1.25	0.88
8	6.70	1.25	7.77	7.95	7.77	0.18	0.00
9	7.26	0.18	7.52	7.44	7.44	0.00	0.00
10	9.64	0.00	7.77	9.64	8.39	1.25	0.62
11	7.00	1.25	7.52	8.25	7.52	0.73	0.00
12	6.43	0.73	7.77	7.16	7.16	0.00	0.00

Rozrząd zasobów wodnych - zadanie alokacji zasobów wodnych

Całkowity odpływ ze zbiornika (T) składa się z trzech składowych: ilości wody przeznaczonej na zapewnienie przepływu nienaruszalnego (X_QN), poboru wody przez zakład przemysłowy (X_P) oraz zrzutu jałowego (ZJ).

Rozrząd wody obywa się zwykle zgodnie z ustaloną hierarchią korzystania z zasobów wodnych.

Rys. 6. Algorytm rozrządu wody pomiędzy użytkowników

Tabela 3. Rozrząd wody pomiędzy użytkowników

Miesiąc	T	Δt	T	XQN	XP	ZJ	Deficyt	Wpadki
	[mln m^3]	[mln s]	[m^3/s]	[m^3/s]	[m^3/s]	[m^3/s]	[m^3/s]
1	2	3	4	5	6	7	8	9
1	7.77	2.68	2.90	0.50	2.40	0.00	0.00	0
2	7.21	2.42	2.98	0.50	2.40	0.08	0.00	0
3	8.84	2.68	3.30	0.50	2.40	0.40	0.00	0
4	7.52	2.59	2.90	0.50	2.40	0.00	0.00	0
5	7.42	2.68	2.77	0.50	2.27	0.00	0.13	1
6	7.52	2.59	2.90	0.50	2.40	0.00	0.00	0
7	8.64	2.68	3.23	0.50	2.40	0.33	0.00	0
8	7.77	2.68	2.90	0.50	2.40	0.00	0.00	0
9	7.44	2.59	2.87	0.50	2.37	0.00	0.03	1
10	8.39	2.68	3.13	0.50	2.40	0.23	0.00	0
11	7.52	2.59	2.90	0.50	2.40	0.00	0.00	0
12	7.16	2.68	2.67	0.50	2.17	0.00	0.23	1
	QN [m^3/s]	P [m^3/s]					Suma=	3
		0.5					2.4					Gt(VU)=	0.75

Gwarancja czasowa spełnienia potrzeb wodnych zakładu przemysłowego wynosi G_t = 0.75 i jest mniejsza do gwarancji wymaganej przez użytkownika (G_kr = 0.80).

Oznacza to, że przyjęta w pierwszym kroku pojemność użytkowa VU = 1.25 mln m³ jest za mała oraz warunek dokładności nie jest spełniony:

należy powtórzyć wszystkie obliczenia dla nowego zakresu zmienności pojemności użytkowej:
.

Nowa pojemność użytkowa wynosi VU = 1.88 mln m³.

Gwarancja czasowa spełnienia potrzeb zakładu przemysłowego odpowiadającą tej pojemności użytkowej wynosi G_t = 1.00.

Przebieg procesu wyznaczania pojemności użytkowej zbiornika, obejmujący 6 iteracji przedstawiono w tabeli 4.

Tabela 4. Wyznaczanie pojemności użytkowej zbiornika

Lp.	VUmin	VUmax	VU	Gt(VU)	VUmax-VUmin
1	0.00	2.50	1.25	0.75	2.50
2	1.25	2.50	1.88	1.00	1.25
3	1.25	1.88	1.56	0.83	0.63
4	1.25	1.56	1.40	0.83	0.31
5	1.25	1.40	1.32	0.75	0.15
6	1.32	1.40	1.36	0.83	0.08
	VU = 1.36 mln m^3

Ostatecznie, w wyniku przeprowadzonych obliczeń stwierdzono, że najmniejsza pojemność użytkowa zbiornika pozwalająca zaspokoić potrzeby zakładu przemysłowego z gwarancją nie mniejszą niż 0.80 wynosi:

Wyznaczanie pojemności zbiornika dla Gt = 1

Zadanie wyznaczania pojemności użytkowej zbiornika znacznie się upraszcza, gdy wymagana przez użytkownika gwarancja czasowa jest równa 1. Algorytm obliczeniowy można zapisać w postaci:

gdzie:

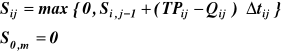
Wyniki obliczeń wykonanych zgodnie z tym algorytmem pokazano w tabeli 5.

Zapewnienie zakładowi przemysłowemu wody we wszystkich rozpatrywanych okresach (miesiącach) będzie możliwe po wybudowaniu zbiornika o pojemności użytkowej:

Tabela 5Wyznaczanie pojemności użytkowej zbiornika metodą uproszczoną dla G_t = 1

Miesiąc	Q	TP=P+QN	TP-Q	S
		[mln m^3]	[mln m^3]	[mln m^3]	[mln m^3]
1	2	4	5	6
0	-	-	-	0.0
1	7.23	7.77	0.54	0.54
2	7.74	7.02	-0.73	0.00
3	8.84	7.77	-1.07	0.00
4	7.26	7.52	0.26	0.26
5	6.43	7.77	1.34	1.60
6	8.04	7.52	-0.52	1.08
7	9.37	7.77	-1.61	0.00
8	6.70	7.77	1.07	1.07
9	7.26	7.52	0.26	1.33
10	9.64	7.77	-1.87	0.00
11	7.00	7.52	0.52	0.52
12	6.43	7.77	1.34	1.86
			VU = 1.86 mln m^3

Zależność gwarancji czasowej G_t = F (TP,VU)

zapewnienia odpływu pożądanego (TP)

od pojemności użytkowej zbiornika (VU) i wielkości tego odpływu.

Zależność taką wyznacza się na podstawie obliczeń symulacyjnych dla różnych poziomów odpływu pożądanego oraz różnych pojemności użytkowych zbiornika

W obliczeniach symulacyjnych rozważano odpływy pożądane w zakresie 2.4 - 2.9 m³/s z krokiem ΔTP = 0.1 m³/s i pojemności użytkowe zbiornika w zakresie 0.0 - 2.5 mln m³ z krokiem ΔVU = 0.1  mln m³. Na wykresie pominięto odpływ pożądany TP = 2.7 m³/s ze względu na czytelność wykresu.

Rys. 7. Wykres zależności gwarancji czasowej odpływu pożądanego od pojemności użytkowej zbiornika i wielkości tego odpływu.

Wyznaczenie przepustowości kanału przerzutowego

Rozwiązanie problemu zaopatrzenia w wodę polega na wyznaczeniu możliwie najmniejszej przepustowości kanału, która umożliwi zaopatrzenie w wodę zakładu przemysłowego z wymaganą gwarancją.

Wyznaczanie przepustowości kanału (QK) w ogólnym przypadku przebiega w podobny sposób jak wyznaczanie pojemności użytkowej zbiornika retencyjnego (porównaj rys. 4).

Zakres zmienności przepustowości można określić w następujący sposób:

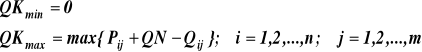
W rozpatrywanym przykładzie potrzeby P_ij są stałe i wynoszą P=2.4 m³/s, w związku z tym wzór na górną granicę zakresu przyjmuje postać:

Minimalna wartość przepływu wynosi 2.4 m³/s, wobec tego QK_max = 0.5 m³/s.

Symulacja pracy systemu zaopatrzenia w wodę (kanału przerzutowego) zależy od przyjętych zasad pracy kanału (np. kanał prowadzi przez cały czas określoną ilość wody lub też kanał uruchamiany jest w trybie interwencyjnym, tzn. tylko w okresach niedoboru wody w przekroju ujęcia wody dla zakładu, itp.).

Załóżmy, że w naszym przykładzie kanał pracuje w trybie interwencyjnym, czyli w zależności od zapotrzebowania przepływ w kanale może zmieniać się od 0 do jego przepustowości (QK).

Symulacja pracy systemu w każdym rozpatrywanym przedziale czasowym (miesiącu) obejmuje obliczenie ilości wody, jaka powinna być dostarczona kanałem, aby w pełni pokryć zapotrzebowanie zakładu przemysłowego (czyli deficyt wody w zakładzie).

Jeżeli deficyt wody (D_ij) w danym przedziale czasowym jest mniejszy lub równy przepustowości kanału, to zostaje on zlikwidowany poprzez doprowadzenie wody kanałem.

W przeciwnym przypadku pomimo pracy kanału deficyt zostaje tylko ograniczony do wielkości: (D_ij - QK).

Przykładowe obliczenia dla przepustowości kanału QK = 0.25 m³/s zamieszczono w tabeli 6.

Kolejne kroki wyznaczania przepustowości kanału przy założeniu, że dokładność obliczeń wynosi ε_QK = 0.05 m³/s pokazano w tabeli 3.7.

W wyniku przeprowadzonych obliczeń ustalono, że kanał przerzutowy powinien mieć przepustowość QK = 0.4 m³/s.

Tabela 6. Symulacja pracy kanału przerzutowego

					QK=	0.25
Rok	Miesiąc	Qij	Pij+QN	Dij= Pij+QN-Qij	Dij-QK	Wpadki
		[m^3/s]	[m^3/s]	[m^3/s]	[m^3/s]
1	1	2.7	2.9	0.2	0	0
1	2	3.2	2.9	0	0	0
1	3	3.3	2.9	0	0	0
1	4	2.8	2.9	0.1	0	0
1	5	2.4	2.9	0.5	0.25	1
1	6	3.1	2.9	0	0	0
1	7	3.5	2.9	0	0	0
1	8	2.5	2.9	0.4	0.15	1
1	9	2.8	2.9	0.1	0	0
1	10	3.6	2.9	0	0	0
1	11	2.7	2.9	0.2	0	0
1	12	2.4	2.9	0.5	0.25	1
				Suma	0.7	3
								Gwarancja czasowa Gt=		0.75

Tabela 7. Wyznaczanie przepustowości kanału przerzutowego

Lp.	QKmin	QKmax	QK	Gt(QK)	QKmax-QKmin
1	0.00	0.50	0.25	0.75	0.50
2	0.25	0.50	0.38	0.75	0.25
3	0.38	0.50	0.44	0.83	0.12
4	0.38	0.44	0.41	0.83	0.06
5	0.38	0.41	0.40	0.83	0.03
	QK = 0.40 m^3/s

W przypadku, gdy potrzeby wodne użytkownika są stałe w czasie, procedura wyznaczania przepustowości kanału znacznie się upraszcza.

W takim przypadku podstawę do wyznaczania przepustowości kanału przerzutowego stanowi (krzywa przepływów gwarantowanych), określająca zależność pomiędzy gwarancją czasową (G_t), a wielkością przepływu gwarantowanego (Q_gw):

Krzywą przepływów gwarantowanych sporządza się w przedziale od Q_min = 2.4 do Q_max = 3.6 m³/s z zadaną dokładnością krokiem np. ΔQ = 0.1 m³/s.

Dla kolejnych wartości przepływu: Q_min, Q_min + ΔQ,..., Q_max oblicza się gwarancje ich występowania ze wzoru:

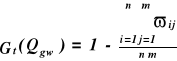
gdzie:
oznacza liczbę okresów, w których przepływ w rzece był mniejszy od rozpatrywanego przepływu gwarantowanego Q_qw.

W tabeli 8 pokazano krzywą przepływów gwarantowanych dla rozpatrywanego przykładu.

Tabela 8. Przepływy gwarantowane

Lp.	Qgw	Gt(Qgw)
	[m^3/s]	[-]
1	2.4	1.00
2	2.5	0.83
3	2.6	0.75
4	2.7	0.75
5	2.8	0.58
6	2.9	0.42
7	3.0	0.42
8	3.1	0.42
9	3.2	0.33
10	3.3	0.25
11	3.4	0.17
12	3.5	0.17
13	3.6	0.08

Z tabeli wynika, że z wymaganą gwarancją G_kr = 0.80 można zapewnić przepływ Q_qw = 2.5 m³/s, co oznacza, że do zaspokojenia potrzeb zakładu przemysłowego i przepływu nienaruszalnego (2.9 m³/s) brakuje 0.4 m³/s i taka powinna być przepustowość kanału.

Warto zauważyć, że wydajność ujęcia wód podziemnych oraz zakres wymaganej redukcji potrzeb poprzez zmianę technologii oblicza się dokładnie tak samo, jak przepustowość kanału przerzutowego.

W przypadku, gdy rozpatrujemy warianty mieszane (np. zbiornik retencyjny i kanał przerzutowy) do określenia parametrów obiektów hydrotechnicznych można wykorzystać zależność gwarancji czasowej odpływu pożądanego od pojemności użytkowej zbiornika i wielkości tego odpływu pokazaną na rys. 7.

Podsumowanie

Omówiony przykład dotyczył najprostszej możliwej do wyobrażenia sytuacji:

1. w systemie występuje tylko jeden użytkownik,

2. stopień zaopatrzenia w wodę charakteryzowany jest tylko jednym kryterium (gwarancja czasowa),

3. analizy prowadzone były w oparciu o historyczny ciąg przepływów,

4. w systemie występował tylko jeden zbiornik retencyjny,

5. zbiornik pracował zgodnie z najprostszym planem dyspozytorskim (polityką standardową).

1

19

VU = 0.5 (VU_min+ VU_max)

Zakres zmienności VU

VU ∈ <VU_min, VU_max>

SYMULACJA PRACY ZBIORNIKA RETENCYJNEGO

zgodnie z założonym planem dyspozytorskim w całym okresie objętym badaniami

WYNIKI SYMULACJI

T_ij - odpływ wody ze zbiornika

VK_ij - napełnienie końcowe zbiornika

X_ij - ilość wody dostarczonej użytkownikowi

D_ij - deficyt wody u użytkownika

WSKAŹNIKI JAKOŚCI PRACY ZBIORNIKA

Np. gwarancja czasowa G_t(VU)

Czy wskaźniki jakości osiągnęły zadowalające wartości?

VU_min = VU

VU_max = VU

VU_max - VU_min < ε_VU

NIE

TAK

NIE

TAK

STOP

VU=0.5(VU_min+VU_max)

X_QN = T

T ≥ QN

NIE

NIE

X_QN = QN

X_P = P

X_P = 0

TAK

X_P = T - QN

T ≤ QN + P

TAK

---