DIPOL ELEKTRYCZNY

Jednym z podstawowych elementów elektrycznej budowy ciał jest dipol elektryczny. Materiały, których cząsteczki są trwałymi dipolami elektrycznymi nazywane są polarnymi. Przykładem takiej cząsteczki może być cząsteczka wody, której strukturę przedstawiono poniżej na rys.1.

Rys.1. Struktura cząsteczki wody.

Natomiast w cząsteczkach ciał niepolarnych, jak zobaczymy, dipole elektryczne mogą być indukowane zewnętrznym polem elektrycznym.

Dipol elektryczny jest układem dwóch elektrycznych ładunków punktowych
równych co do wartości lecz przeciwnego znaku, oddalonych od siebie na odległość
. Dla scharakteryzowania dipola wprowadza się wielkość wektorową nazywaną elektrycznym momentem dipolowym

.

Wektor
jest wektorem odległości wzajemnej ładunków dipola skierowanej od ładunku ujemnego dipola do dodatniego. Pole wytwarzane przez dipol, a także siły działające na dipol, zależą od jego elektrycznego momentu dipolowego — są takie same dla dwu różnych dipoli posiadających ten sam moment dipolowy. Pole elektryczne dipola w dużej odległości
od niego można obliczyć sumując wektorowo pola kulombowskie pochodzące od obu ładunków punktowych.

Dla
na osi dipola otrzymujemy

.

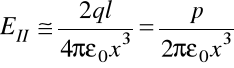
W kierunku prostopadłym do osi przy
pole ma natężenie dwukrotnie mniejsze

.

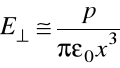
Jest zrozumiałe, że pole elektryczne dipola, jako obiektu o łącznym ładunku równym zeru, maleje szybciej z odległością (
) niż pole ładunku punktowego
).

W jednorodnym zewnętrznym polu elektrycznym o natężeniu
działa na dipol moment siły
(rys.2), wartość którego
(moduł wektora) określamy wzorem

,

gdzie
jest kąt między wektorami
a
.

Rys.2. Dipol w polu jednorodnym

W postaci wektorowej z wykorzystaniem iloczynu wektorowego mamy

.

Jeśli dipol elektryczny jest swobodny to zewnętrzne pole ustawi go w kierunku zgodnym z polem (zwrot
zgodny z
).

Obrót dipola w zewnętrznym polu elektrycznym wymaga wykonania pracy

.

Można przyjąć, że to wyrażenie podaje wartość energii potencjalnej dipola w zewnętrznym polu elektrycznym. Wtedy dipol tworzący z polem kąt
ma energię potencjalną najmniejszą
. Przy kącie
energia potencjalna będzie miała wartość zerową, a przy
wartość maksymalną
.

W polu zewnętrznym niejednorodnym swobodny dipol zostanie najpierw obrócony do pokrycia się zwrotów momentu dipolowego i pola a wtedy będzie wciągany do obszaru gdzie pole jest silniejsze (rys.3).

Załóżmy, że w środku dipola natężenie pola równe jest
. Wtedy w miejscach gdzie znajdują się ładunki

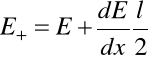
i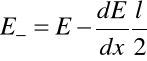

Siła działająca na dipol będzie zatem równa

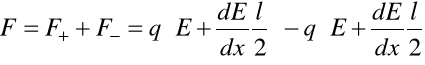
Rys.3. Dipol w polu niejednorodnym

Po przekształceniach

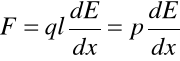
Pochodna
jest w tym wzorze miarą niejednorodności pola.

DIELEKTRYKI

Dielektryki w polu elektrostatycznym

Elektrony w dielektryku nie mogą się swobodnie przemieszczać. Ograniczone są przez atomy i cząsteczki, których nie mogą opuścić.

Ale jeżeli umieścimy dielektryk w polu elektrostatycznym między ładunkiem dodatnim a ujemnym to ułożenie elektronów i jąder atomowych zmienia się. Elektrony ustawiają się tak by być jak najbliżej ładunku dodatniego, a jądra jak najbliżej ładunku ujemnego. Te cząsteczki zachowują się jak dipole. Ułożenie takie wykazują wszystkie cząsteczki w dielektryku. Tak tworzy się łańcuch dipoli z ładunkami dodatnimi skierowanymi z jednej strony, a ujemnymi skierowanymi w drugą stronę. Takie zjawisko nazywamy polaryzacją dielektryka.

Spolaryzowany dielektryk tworzy własne pole wewnętrzne, którego wektor natężenia jest zawsze skierowany przeciwnie do wektora natężenia pola, w którym umieszczony został dielektryk. W ten sposób zmniejszane jest wypadkowe natężenie pola. Makroskopowo zjawisko polaryzacji dielektryka postrzegamy jako gromadzenie się ładunków na powierzchni dielektryka (obojętnego jako całość).

Jeżeli dielektryk umieścimy między okładkami naładowanego kondensatora, to zmniejszy się w ten sposób napięcie tego kondensatora, ponieważ występuje związek

.

Jeżeli napięcie zmniejsz się to zwiększy się pojemność kondensatora

,

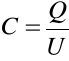
ponieważ ładunek pozostaje przecież taki sam.

Wykorzystując te wiadomości możemy badać względną przenikalność dielektryczną substancji z której zbudowany jest dielektryk. Niech
to pojemność kondensatora z próżnią między płytkami (z powietrzem), natomiast
to pojemność kondensatora z dielektrykiem między płytkami. Wtedy po prostych obliczeniach otrzymamy

.

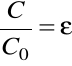
Stosunek pojemności kondensatora z dielektrykiem do pojemności kondensatora z próżnią między okładkami jest względną przenikalnością dielektryczną dielektryka.

Rozróżnia się dialektryki niepolarne i polarne.

Molekuły dielektryków niepolarnych nie posiadają własnych trwałych elektrycznych momentów dipolowych. Przykładem takich dielektryków są
. Polaryzacje ośrodka możemy określić przez wzór

,

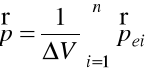
gdzie wektor polaryzacji
poszczególnych molekuł jest jednakowy dla wszystkich molekuł, które znajdują się w objętości
, i wprost proporcjonalny do natężenia zewnętrznego pola elektrycznego

,

gdzie
— współczynnik proporcjalności (polaryzowalność).

Obliczamy

,

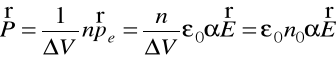
gdzie
— gęstość molekuł.

Określając podatność elektryczna (dielektryczna)

,

otrzymamy

.

Molekuły dielektryków polarnych posiadają własne trwałe elektryczne momenty dipolowe. Przykładem takich dielektryków są
. Wektor polaryzacji jest również wprost proporcjonalny do natężenia pola elektrycznego

,

gdzie
— polaryzowalność.

INDUKCJA ELEKTRYCZNA

Indukcja elektryczna
jest zdefiniowana jako

,

albo wyrażona przez wzór

,

gdzie
— przenikalność elektryczna materiału.

W ośrodkach nieliniowych przenikalność elektryczna zależy od natężenia pola elektrycznego, może także zależeć od wcześniejszych wartości natężenia pola elektrycznego, takie własności wykazują ferroelektryki.

W ośrodkach anizotropowych wektory natężenia i indukcji pola elektrycznego mogą nie być równoległe, przenikalność elektryczna jest nie jest wówczas tensorem. Oznacza to, że w ośrodku takim przenikalność ma różne wartości w różnych kierunkach. To pociąga za sobą różnicę w prędkości rozchodzenia się światła (patrz związek powyżej) - a zatem i współczynnika załamania - zależnie od kierunku polaryzacji światła. Zjawisko to nazywa się podwójnym załamaniem albo dwójłomnością. Spośród substancji naturalnych zjawisko dwójłomności wykazuje między innymi kalcyt.

Warunki brzegowe.

Składowa styczna wektora natężenia pola
jest ciągła

.

Składowa normalna wektora indukcji (przesunięcia dielektrycznego) jest ciągła, jeżeli na powierzchni granicznej nie ma ładunków swobodnych

.

Dla dialektyka mamy

,
.

Łatwo zauważyć, że na granicy dwóch dielektryków następuje załamanie linii natężenia pola elektrycznego linii indukcji.

Pojemność elektryczna: Jeżeli dostarczymy ładunek
odizolowanemu przewodnikowi, to wzrasta również jego potencjał elektryczny
, przy czym wzrost potencjału jest proporcjonalny do dostarczonego ładunku. Stosunek tego ładunku do potencjału przewodnika, nazywamy pojemnością elektryczną C, co wyrażamy wzorem

.

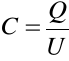
Jednostką pojemności jest farad (F) — pojemność ciała, przekazanie któremu dostarczenie ładunku 1 kulomba powoduje wzrost potencjału o 1 wolt.

Energia przewodnika naładowanego: Energia przewodnika naładowanego ładunkiem
jest równa pracy jaką trzeba wykonać, aby zgromadzić ładunek na przewodniku doprowadzając go w bardzo małych porcjach z nieskończoności.

Doprowadzenie ładunku
zwiększa energiì potencjalną przewodnika o

,

gdzie
— aktualny potencjał przewodnika.

Wtedy

.

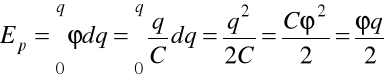
Energia naładowanego kondensatora: Energię naładowanego kondensatora można obliczyć podobnie jak energie naładowanego przewodnika z tym, że teraz obliczamy pracę przeniesienia ładunku swobodnego z jednej okładki na drugą.

Praca elementarna

,

gdzie
— aktualna różnica potencjału kondensatora.

Wtedy

.

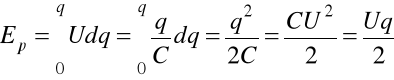
Energia pola elektrycznego: Wyraźmy energie naładowanego kondensatora płaskiego poprzez natężenie pola elektrycznego między okładkami. Skorzystamy ze wzoru dla pojemności płaskiego kondensatora

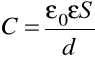
oraz jego energii

.

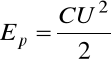
Otrzymamy

.

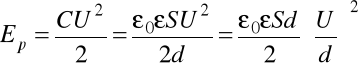
Ponieważ

i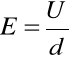
,

to

.

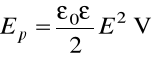
Energiì tę można rozumieć jako energie pola elektrycznego zawartego w kondensatorze. Jej gęstość wynosi

.

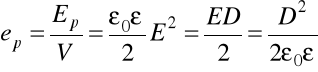
Możemy też zapisać

.

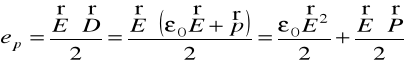
Wówczas dokonamy takiej interpretacji:

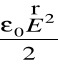
— gęstość energii pola w próżni,

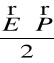
— energia polaryzacji jednostki objętości dielektryka.

---