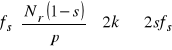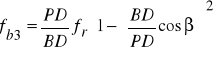1. Drgania mechaniczne - wielkości charakterystyczne
Stan każdej maszyny i jej elementów można ocenić na podstawie drgań występujących w czasie jej pracy. Dotyczy to również maszyn elektrycznych. Podczas pracy maszyny elektrycznej mogą wystąpić drgania okresowe i nieokresowe. Drgania okresowe mogą mieć przebieg sinusoidalny lub odkształcony. Drgania nieokresowe mogą powstać od przyczyn występujących doraźnie.
Drgania maszyny elektrycznej mogą być spowodowane przyczynami zewnętrznymi lub przyczynami istniejącymi w samej maszynie. Przyczynami zewnętrznymi mogą być: drgania maszyny współpracującej, niewłaściwe sprzęgnięcie z maszyną współpracującą lub niewłaściwe ustawienie na płycie fundamentowej. Drgania maszyny elektrycznej wywołane drganiami maszyny współpracującej występują np. przy współpracy maszyny elektrycznej z maszyną tłokową. Wewnętrznymi przyczynami drgań maszyny elektrycznej mogą być na przykład: asymetria magnetyczna, naciąg magnetyczny, wady łożysk, brak wyważenia wirnika.
Drgania okresowe mogą być rozpatrywane jako ruch oscylacyjny punktu materialnego lub ciała względem pozycji odniesienia. Ruch ten dokładnie powtarza się po pewnych okresach czasu. Najprostszą formą drgań okresowych jest tak zwany ruch harmoniczny, którego wykres w funkcji czasu reprezentowany jest przez sinusoidę (rys. 1). Okres wibracji T jest czasem upływającym pomiędzy dwoma następującymi po sobie jednakowymi stanami ruchu.
Przykład sygnału przemieszczenia drgań ruchu harmonicznego
Częstotliwość drgań określona jest wzorem:
![]()
(1)
Zmiana amplitudy drgań może być scharakteryzowana przez trzy, ściśle ze sobą powiązane, wielkości: przemieszczenie x, prędkość v i przyspieszenie drgań a.
Jeżeli wibracje mają charakter drgania wzdłuż jednej osi to chwilowe przemieszczenie punktu materialnego bądź ciała względem pozycji odniesienia, jest opisane równaniem:
![]()
(2)
gdzie: ω = 2·π·f - prędkość kątowa [1/s],
xm - wartość szczytowa przemieszczenia drgań [m],
t - czas [s].
Prędkość ruchu punktu materialnego lub ciała jest zmianą przemieszczenia w czasie, więc drgania mogą być również opisane przy pomocy prędkości:
![]()
(3)
Przyspieszenie jest zmianą prędkości w czasie więc drgania można opisać następująco:
![]()
(4)
Wielkości opisujące drgania związane są ze sobą zależnościami przedstawionymi w tabeli 1.
Przekształcanie wielkości przemieszczenia, prędkości i przyspieszenia drgań
Przebieg czasowy wielkości fizycznych charakteryzujących drgania. a) przemieszczenie drgań, b) prędkość drgań, c) przyspieszenie drgań
Zależność obwiedni wielkości fizycznych charakteryzujących drgania od częstotliwości
Przykład przebiegu harmonicznego ze wskazaniem wartości szczytowej xm, wartości skutecznej xsk, oraz wartości średniej xsr
Przykładowy nie-harmoniczny ruch okresowy (przyspieszenie tłoka silnika spalinowego)
Ilustracja rozkładu Fouriera dla sygnału przedstawionego na rysunku 5
Przykład sygnału opisanego w dziedzinie czasu (a), oraz w dziedzinie częstotliwości (b)
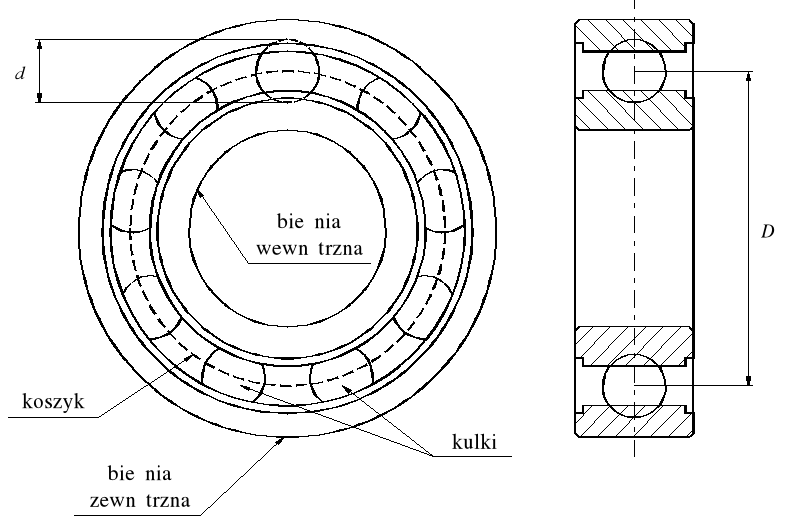
Łożysko toczne kulkowe, zwykłe; d - średnica elementu tocznego, D - średnica podziałowa łożyska
Przykładowe prążki widma drgań maszyny elektrycznej (częstotliwości związane z uszkodzeniami łożyska przedstawiono dla łożyska dziewięciokulkowego); fs - częstotliwość napięcia zasilającego, fzw - częstotliwość pochodząca od układów zewnętrznych (np. sprzęgła, przekładni)
Dane znamionowe badanego silnika
Dane konstrukcyjne łożyska kulkowego typu 6205ZZ
Rodzaje uszkodzeń badanych łożysk
Łożysko kulkowe typu 6205ZZ
Multianalizator Pulse typu 3560
Miniaturowy akcelerometr piezoelektryczny z wbudowanym przedwzmacniaczem DeltaTron typ 4397
Miniaturowy trójosiowy akcelerometr piezoelektryczny z wbudowanym przedwzmacniaczem DeltaTron typ 4506
Wyniki pomiarów drgań
Parametry pomiarów w systemie Pulse
|
|
Przemieszczenie drgań |
Prędkość drgań |
Przyspieszenie drgań |
Przemieszczenie drgań |
x = |
1 |
|
|
Prędkość drgań |
v = |
|
1 |
|
Przyspieszenie drgań |
a = |
|
|
1 |
Na podstawie zależności (1-4) widać, że kształt i okres drgań są takie same niezależnie od rozpatrywanej wielkości. Jednakże, faza prędkości drgań wyprzedza fazę przemieszczenia o kąt 90°, a przyspieszenie wyprzedza prędkość o kolejne 90° (rys 2).
|
|
|
|
Ponieważ wielkości opisujące drgania związane są prostymi zależnościami łatwo jest je przeliczać a co za tym idzie nie ma większego znaczenia, która z tych wielkości jest rejestrowana w pomiarach. Wybór parametru drgań ma jednak znaczenie przy analizie drgań (rys. 3). Przemieszczenie drgań najlepiej odzwierciedla drgania w zakresie niskich częstotliwości, dla maszyn wolnoobrotowych poniżej 600 obr/min (10 Hz), ponieważ niskie częstotliwości drgań charakteryzują się wysokimi przemieszczeniami. Prędkość drgań najlepiej odzwierciedla stan maszyny przy częstotliwościach drgań od ok. 30 Hz do 1500 Hz, natomiast przyspieszenie drgań przy wysokich częstotliwościach.
Drugą istotną sprawą przy analizie drgań jest wybór skali amplitudy. Stosuje się liniowe i logarytmiczne skale amplitud. Skala logarytmiczna (decybelowa) jest bezwymiarowa i wyraża stosunek danego poziomu do poziomu odniesienia.
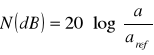
(5)
gdzie: N - ilość decybeli,
a - poziom mierzony,
aref - poziom odniesienia.
Skala logarytmiczna uwypukla harmoniczne o niskich wartościach amplitud. Jest ona zatem przydatna podczas analizy badanych wibracji o małych wartościach. Skala liniowa nadaje się lepiej do badań, w których dla analizy ważne są harmoniczne o wysokich amplitudach, gdyż na wykresie w tej skali widoczne będą tylko wierzchołki dominujących harmonicznych.
Jako wartość charakteryzującą amplitudę używa się wartości szczytowej. Opis amplitudy jako wartości szczytowej jest słuszny, jeśli wibracja ma charakter czysto sinusoidalny (harmoniczny). To założenie przyjęto w równaniach (2-4). Bardziej złożone wibracje są analizowane przy innych definicjach wielkości charakterystycznych. Podstawowym powodem jest fakt, że amplituda jest zmienna w czasie, więc nie określa wartości szczytowej.
Kolejną wielkością opisującą sygnał w dziedzinie czasu jest wartość średnia definiowana jako:
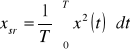
(6)
Użycie wartości średniej w przypadku przebiegów harmonicznych, gdy rozpatrywane są pełne okresy przebiegu, nie ma sensu gdyż wynosi ona zero. Praktyczne znaczenie może mieć w przypadku przebiegów nieharmonicznych. Znacznie wygodniejszą wielkością opisującą przebiegi w dziedzinie czasu jest wartość skuteczna:
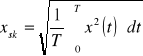
(7)
Głównym powodem, dla którego wartość skuteczna jest ważną wielkością przy opisie drgań jest jej proporcjonalność do energii drgań.
Na rysunku 4 przedstawiono powiązania omawianych wielkości charakterystycznych.
Dla przebiegów harmonicznych obowiązują następujące powiązania między omawianymi wartościami:
![]()
(8)
W przypadku bardziej ogólnym:
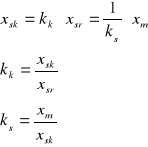
(9)
Współczynniki, kształtu kk i szczytu ks dają informacje na temat kształtu fali rozpatrywanych drgań. Dla ruchu harmonicznego wynoszą one:
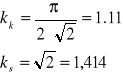
(10)
Spośród mierzonych w praktyce sygnałów wibracyjnych większa część nie jest czystymi drganiami harmonicznymi, mimo że większość z nich można scharakteryzować jako periodyczne. Typowy przebieg odkształcony przedstawiono na rysunku 5.
Analizując wartości: szczytową, średnią i skuteczną, badanego ruchu wibracyjnego oraz współczynniki kształtu i szczytu uzyskuje się wiele użytecznych informacji i łatwo można wyciągnąć wniosek że ruch nie jest harmoniczny. Jednakże, praktycznie niemożliwe jest przewidywanie na podstawie tych informacji wszystkich skutków, które wibracje mogą wywołać w badanej strukturze. Dlatego do analizy drgań używa się innych metod na podstawie których można prognozować skutki wibracji.
Jedną z najbardziej użytecznych metod opisu drgań jest metoda Fouriera (analizy częstotliwości) mówiąca, że każda krzywa okresowa, niezależnie od stopnia odkształcenia może być rozpatrywana jako kombinacja sinusoidalnych krzywych o odpowiednich częstotliwościach.
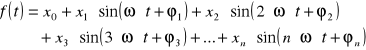
(11)
Liczba składników potrzebnych do odtworzenia badanego sygnału może być nieskończona. Im większa liczba składników tym lepsza aproksymacja oryginalnej krzywej. Poszczególne składniki tworzą widmo częstotliwości drgań. Na rysunku 6 przedstawiono odkształcony przebieg periodyczny z rysunku 5 wraz z dwoma najważniejszymi przebiegami harmonicznymi. Rysunek 7 przedstawia fragment przykładowego sygnału wraz z jego widmem częstotliwości. Widmo składa się z prążków amplitud odpowiednich częstotliwości.
|
|
2. Diagnostyka łożysk oparta o analizę widmową drgań maszyny
Uszkodzenie łożyska powoduje pojawienie się w sygnale drganiowym szeregu impulsów z częstotliwością powtarzania zależną od geometrii i kinematyki łożyska. Skład widmowy jednego impulsu jest zależny od charakterystyki geometrycznej uszkodzenia oraz transmitancji układu między źródłem i punktem odbioru sygnału. Częstotliwości odpowiadające defektom elementów łożyska tocznego można obliczyć w oparciu o zależności:
![]()
(12)
![]()
(13)
![]()
(14)
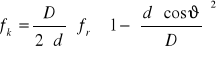
(15)
![]()
(16)
gdzie: fr - częstotliwość obrotowa,
flk - częstotliwość związana z uszkodzeniem i luzami koszyka,
fbz - częstotliwość związana z uszkodzeniem bieżni zewnętrznej,
fbw - częstotliwość związana z uszkodzeniem bieżni wewnętrznej,
fk - częstotliwość związana z uszkodzeniem elementu tocznego,
n - prędkość obrotowa maszyny,
d - średnica elementu tocznego,
D - średnica podziałowa łożyska,
ϑ - kąt pracy łożyska - 0° (dla łożyska kulkowego zwykłego),
Nk - liczba elementów tocznych łożyska.
Wymiary łożysk niezbędne do wyznaczenia częstotliwości charakteryzujących uszkodzenia poszczególnych elementów łożyska przedstawiono na rysunku 8.
Na rysunku 9 przedstawiono przykładowe widmo drgań maszyny z zaznaczeniem częstotliwości powstających w wyniku uszkodzenia elementów łożyska.
Poziom drgań uszkodzonych łożysk rośnie wraz z jego zużyciem i może radykalnie się obniżyć tuż przed awarią. Drgania występują na łożyskach w płaszczyźnie promieniowej z wyjątkiem łożyska oporowego, gdzie również występują w kierunku osiowym. We wczesnych stanach degradacji łożyska składowe drgań charakteryzują się dużymi częstotliwościami drgań (powyżej 500Hz). W późniejszych stanach rośnie pierwsza harmoniczna oraz jej wielokrotności.
Ponieważ uszkodzone łożyska toczne generują drgania szerokopasmowe, dla wykrywania defektów w jeszcze bardzo wczesnej fazie, zaleca się pomiary przyspieszenia drgań. Można rejestrować wartości skuteczne i wartości szczytowe przyspieszeń w celu ich porównania. Stosunek wartości szczytowej do wartości skutecznej nazywa się współczynnikiem szczytu a jego wartość może być estymatą stanu łożyska.
3. Diagnostyka łożysk oparta o analizę widmową prądu stojana
Również widmo prądu stojana silnika zawiera harmoniczne charakterystyczne dla poszczególnych rodzajów uszkodzeń łożyska i dla tego można na jego podstawie określać stopień i rodzaj uszkodzenia. Widmo prądu stojana, idealnego nie uszkodzonego silnika posiada tylko podstawową harmoniczną napięcia zasilającego fs. Zmiany obciążenia silnika modulują amplitudę prądu wytwarzając oprócz harmonicznej podstawowej dodatkowe składowe częstotliwości. Drgania pochodzące od uszkodzonego łożyska powodują zmianę wielkości szczeliny powietrznej między wirnikiem a stojanem. Powoduje to powstanie dodatkowych harmonicznych nie związanych z harmoniczną podstawową napięcia zasilania. Na podstawie analizy częstotliwościowej można wyznaczyć składowe częstotliwości prądu odpowiadające poszczególnym typom uszkodzeń w łożysku.
![]()
(17)
gdzie: k=1,2,3,...,
fu - częstotliwość prądu związana z danym uszkodzeniem łożyska,
fs - częstotliwość napięcia zasilającego,
fl - częstotliwości związane z uszkodzeniem łożyska (fk, fbz, fbw, flk obliczone według zależności 12 - 15).
4. Badania drgań i prądów silnika indukcyjnego z uszkodzonymi łożyskami
Badany silnik
W badaniach łożysk wykorzystano silnik indukcyjny, trójfazowy, małej mocy o danych zestawionych w tabeli 2.
Producent |
INDUKTA |
|
Typ |
typ SSh-90L-4 |
|
Nr fabryczny |
423347 |
|
Napięcie |
220/380 |
V |
Prąd |
6,4/3,7 |
A |
Moc |
1,5 |
kW |
Prędkość obrotowa |
1410 |
obr/min |
Współczynnik mocy cosϕ |
0,78 |
|
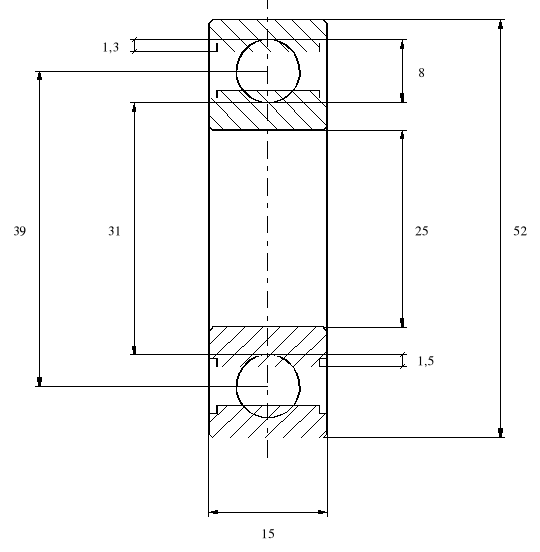
Badane łożyska
W badaniach użyto 20 łożysk kulkowych zwykłych typu 6205ZZ. Budowę łożyska przedstawiono na rysunku 10 a jego dane w tabeli 3. Łożyska uszkodzono stopniując wielkość uszkodzenia poszczególnych jego elementów. W efekcie uzyskano sześć łożysk z uszkodzoną w różnym stopniu bieżnią zewnętrzną, cztery łożyska z uszkodzoną bieżnią wewnętrzną, cztery łożyska z uszkodzoną kulką i dwa zużyte łożyska z różnymi uszkodzeniami przeznaczone do testowania detektora neuronowego. Ponadto przebadano cztery nowe łożyska w celu uzyskania bazy odniesienia dla łożysk uszkodzonych. Sposób i stopień uszkodzenia poszczególnych łożysk podano w tabeli 4.
średnica kulki |
dk |
8 |
mm |
średnica koszyka |
dko |
39 |
mm |
liczba kulek |
Nk |
9 |
szt. |
kąt pracy łożyska |
ϑ |
0 |
deg |
Nr |
Typ uszkodzenia |
Opis uszkodzenia |
1 |
Łożysko z uszkodzoną bieżnią zewnętrzną |
Pęknięty pierścień zewnętrzny |
2 |
Łożysko z uszkodzoną bieżnią zewnętrzną |
Dwa nacięcia w pierścieniu zewnętrznym (wąskie i szerokie) |
3 |
Łożysko z uszkodzoną bieżnią zewnętrzną |
Szerokie nacięcie w pierścieniu zewnętrznym |
4 |
Łożysko z uszkodzoną bieżnią zewnętrzną |
Szerokie nacięcie w pierścieniu zewnętrznym |
5 |
Łożysko z uszkodzoną bieżnią zewnętrzną |
Wąskie nacięcie w pierścieniu zewnętrznym |
6 |
Łożysko z uszkodzoną bieżnią zewnętrzną |
Wąskie nacięcie w pierścieniu zewnętrznym |
7 |
Łożysko z uszkodzoną kulką |
Uszkodzone dwie kulki obok siebie |
8 |
Łożysko z uszkodzoną kulką |
Kulka mocno uszkodzona w wielu miejscach |
9 |
Łożysko z uszkodzoną kulką |
Kulka uszkodzona w wielu miejscach |
10 |
Łożysko z uszkodzoną kulką |
Kulka uszkodzona w jednym miejscu |
11 |
Łożysko z uszkodzoną bieżnią wewnętrzną |
Szerokie rozcięcie pierścienia wewnętrznego |
12 |
Łożysko z uszkodzoną bieżnią wewnętrzną |
Pęknięty pierścień wewnętrzny (wąskie pęknięcie) |
13 |
Łożysko z uszkodzoną bieżnią wewnętrzną |
Wąskie rozcięcie pierścienia wewnętrznego |
14 |
Łożysko z uszkodzoną bieżnią wewnętrzną |
Nawiercony duży otwór w pierścieniu wewnętrznym |
15 |
Łożysko ogólnie zużyte |
Nieznane uszkodzenia wynikające ze zużycia |
16 |
Łożysko ogólnie zużyte |
Nieznane uszkodzenia wynikające ze zużycia |
17 |
Łożysko nieuszkodzone |
Nowe łożysko |
18 |
Łożysko nie uszkodzone |
Nowe łożysko |
19 |
Łożysko nie uszkodzone |
Nowe łożysko |
20 |
Łożysko nie uszkodzone |
Nowe łożysko |
Opis stanowiska pomiarowego i akcelerometrów
Do badania drgań i prądu stojana oraz ich analizy harmonicznej (FFT) użyto multianalizatora Pulse typ 3560 firmy Brüel&Kjær przedstawionego na rysunku 11. W skład multianalizatora Pulse w użytej konfiguracji wchodzą: komputer osobisty klasy Pentium z kartami procesorów sygnałowych ZD 0812 i dyskiem o pojemności 2 GB do bezpośredniego zapisu danych, układ akwizycji danych typu 2825 z modułem interfejsu analizatora (7521) i czterokanałowym modułem wejściowym, kabel TAXI do komunikacji wewnętrznej (3022) oraz oprogramowanie „Pulse LabShop” w wersji 6. Pomiar prądu zrealizowano przy pomocy przetwornika prądowego LEM typu LA 55-P 50 A/50 mA, a pomiar drgań akcelerometrami firmy Brüel&Kjær. Jeden z używanych przetworników drgań to miniaturowy akcelerometr piezoelektryczny z wbudowanym przedwzmacniaczem DeltaTron typ 4397 przedstawiony na rysunku 12, a drugi to również piezoelektryczny i z wbudowaną elektroniką lecz trójosiowy DeltaTron typ 4506 (rys.13).

System Pulse umożliwia wybór liczby linii (próbek) dla rekordu czasowego oraz zakresu częstotliwości. Możliwe liczby linii to 50, 100, 200, 400, 800, 1600, 3200 lub 6400. W większości przypadków korzystna jest duża liczba linii gwarantująca najlepszą rozdzielczość częstotliwości. Zakres częstotliwości może być ustalony na 1.56, 3.13, 6.25, 12.5, 25, 50, 100, 200, 400, 800 1600, 3200, 6400, 12800, 25600 Hz.
Wybrane wartości liczby linii i zakresu częstotliwości determinują rozdzielczość częstotliwości (f) i długość rekordu (T). Rozdzielczość częstotliwości definiuje się jako stosunek zakresu do liczby linii, a długość rekordu to odwrotność rozdzielczości.
Parametry wykonanych pomiarów zestawiono w tabeli 5.
Akcelerometr |
4397 |
4506 |
||||
Liczba linii |
6400 |
3200 |
||||
Zakres [Hz] |
200 |
400 |
1600 |
200 |
400 |
1600 |
Rozdzielczość [mHz] |
31,25 |
62,5 |
250 |
62,5 |
125 |
500 |
Czas [s] |
32 |
16 |
4 |
16 |
8 |
2 |
ZAŁĄCZNIKI
Tabela Z1. Zestawienie podstawowych uszkodzeń silnika indukcyjnego oraz ich symptomów
w widmie prądu stojana
Rodzaj uszkodzenia |
Częstotliwości charakterystyczne |
Uwagi |
uszkodzenie wirnika klatkowego (przerwane pręty lub pierścień zewnętrzny) |
gdzie: k=1,2,3,… |
w widmie prądu stojana |
|
|
w widmie wektora przestrzennego prądu stojana |
ekscentryczność wirnika |
gdzie: k=1,2,3,… Nr - liczba prętów wirnika nw=1,3,5,7,… nd=0 - przy ekscentryczności statycznej nd=1 - przy ekscentryczności dynamicznej |
ogólna postać uwzględniająca ekscentryczność statyczną i dynamiczną
|
|
|
ekscentryczność dynamiczna |
|
|
ekscentryczność statyczna |
nieosiowość |
|
|
uszkodzenia łożysk
|
|
w przybliżeniu:
nb - liczba elementów tocznych |
niewyważenie statyczne i dynamiczne |
|
|
Tabela Z2 Zestawienie podstawowych uszkodzeń silnika indukcyjnego oraz ich symptomów
w widmie drgań mechanicznych
Rodzaj uszkodzenia |
Częstotliwości charakterystyczne |
Uwagi |
Uszkodzenie wirnika klatkowego |
gdzie: k=1,2,3,… |
Dominujący kierunek osiowy (horyzontalny) |
Ekscentryczność |
gdzie: k=1,2,3,… Nr - liczba prętów wirnika |
Ekscentryczność statyczna |
|
|
Ekscentryczność dynamiczna oraz harmoniczne żłobkowe |
Nieosiowość a) równoległa lub kątowa b) luzy łożysk |
głównie:
czasami: |
Maksymalne w kierunku osiowym Czasami wszystkie harmoniczne fr |
Uszkodzenia łożysk tocznych
a)bieżnia zewnętrzna b) bieżnia wewnętrzna
c) elementy toczne
d) koszyk |
gdzie:
przy czym: nb - liczba elementów
tocznych, PD - średnica podziałowa łożyska. |
Charakterystyczne częstotliwości rezonansowe dla poszczególnych elementów łożysk oraz drgania wysokoczęstotliwościowe 20-60 Hz |
Niewyważenie statyczne i dynamiczne |
|
Największe w kierunku promieniowym |
Uszkodzenia stojana |
|
|
Wyszukiwarka
Podobne podstrony:
Instrukcja drgania 1, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem, Mate
!!! Zagadnienia, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem, Opracowan
Pytanie nr 9, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem, Opracowane z
zag 1 i 5, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem, Opracowane zaga
Laboratorium Diagnostyki, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem,
DIAGNOSTYKA, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem
PODSTA~1, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem, Opracowane zagad
Sprawko wektor przestrzenny, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w prze
stopa, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem, Opracowane zagadnie
Pytanie nr 4, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem, Opracowane z
DIAGNOSTYKA pyt 5, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem, Opracow
diagnostyka wszystko, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem, Opra
wektor przestrzenny- syst.mon i diagn, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i dia
rownania nieliniowe, Automatyka i robotyka air pwr, VI SEMESTR, Notatki.. z ASE, metody numeryczne,
stany awaryjne, Automatyka i robotyka air pwr, VI SEMESTR, Notatki.. z ASE, naped elektrryczny lab,
Metody numeryczne 8, Automatyka i robotyka air pwr, VI SEMESTR, Metody numeryczne
analogowe sprawko cw B, Automatyka i robotyka air pwr, VI SEMESTR, Analogowe i cyfr. syst. pom
30, Automatyka i robotyka air pwr, VI SEMESTR, Notatki.. z ASE, Automatyka 20zabezpieczeniowa 20-%20
więcej podobnych podstron