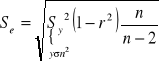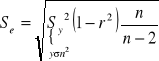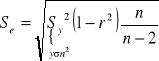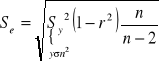Analiza współzależności

Współzależność cech ilościowych

Zadanie 1 Badano wiek w latach kobiet i mężczyzn zawierających związek małżeński, w tym celu wylosowano 10 par i otrzymano następujące dane o wieku (w latach) kobiet (X_i) i mężczyzn (Y_i):

Lp.	Xi	Yi				^2	^2	X^2i	Y^2i	Xi Yi
1	23	27	-2	-2	4	4	4	529	729	621
2	24	28	-1	-1	1	1	1	576	784	672
3	29	30	4	1	4	16	1	841	900	870
4	27	30	2	1	2	4	1	729	900	810
5	33	35	8	6	48	64	36	1089	1225	1155
6	29	41	4	12	48	16	144	841	1681	1189
7	19	22	-6	-7	42	36	49	361	484	418
8	22	25	-3	-4	12	9	16	484	625	550
9	21	26	-4	-3	12	16	9	441	676	546
10	23	26	-2	-3	6	4	9	529	676	598
Razem	250	290	X	X	179	170	270	6420	8680	7429

1. Przedstawić graficznie badaną zależność. (Wykonać diagram zależności Y=X)

2. Na podstawie rozrzutu punktów na diagramie korelacyjnym można scharakteryzować:

1. rodzaj....................................................

2. kierunek.....................................................

3. kształt ………………………………….

4. siłę.....................................................

między badanymi zmiennymi.

3. Badane zmienne to ....................................................................., które mają charakter .......................................

4. Do oceny współzależności zmiennych (cech) ilościowych służy współczynnik korelacji liniowej Pearsona

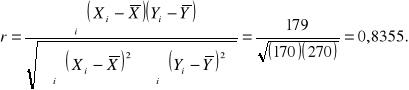
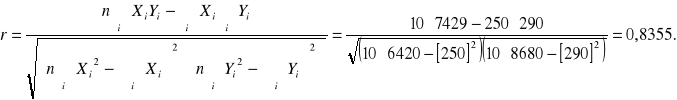
Zadanie 1a (zadanie domowe) W pewnej firmie produkcyjnej badano zależność zużycia głównego surowca od wielkości produkcji i otrzymano informacje zgodnie z poniższą tabelą. Wykonać polecenia z zadania 1.

Lp.	1	2	3	4	5	6	7	8	9	10	11	12
Zużycie surowca w tonach (Xi)	1	2	3	4	5	6	7	8	9	10	11	12
Wielkość produkcji w tys. kg (Yi)	8	10	13	18	20	21	22	24	25	27	30	32

Współzależność cech porządkowych

Zadanie 2 Oceniano kredyty bankowe na zakup nowego samochodu uwzględniano m.in. wysokość miesięcznej raty kredytu oraz wysokość prowizji bankowej.

1. Badane zmienne to ......................................................................, które mają charakter .....................................

2. Do oceny współzależności zmiennych (cech) o charakterze porządkowym służy

współczynnik korelacji liniowej rang ..........................................którego wartość wynosi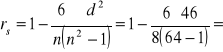
.............

Nazwa banku	Wysokość miesięcznej raty (Xi)	Pozycja wg miesięcznej raty (r1i)	Prowizja bankowa w zł (Yi)	(r2i)	di^2=(r1i-r2i)^2
A	200	1=min	600	4	9
B	210	2	400	2	0
C	225	3	500	3	0
D	250	4	800	6	4
E	260	5	1000	7	4
f	265	6	350 (min ranga 1)	1	25
H	300	7	700	5	4
L (n=8)	320	8	1200	8	0
Razem	X	X	X	X	46

Zadanie 2a Dla ustalonych jednakowych warunków kredytu mieszkaniowego badano w poszczególnych bankach konkurencyjność ofert uwzględniając m.in. wysokość miesięcznej raty kredytu oraz wysokość prowizji bankowej w wybranych bankach. Otrzymano następujące informacje:

Nazwa banku	Pozycja wg miesięcznej raty (r1i)	Prowizja bankowa w zł	(r2i)	di^2=(r1i-r2i)^2
M-bank	1-najwyższa rata	200
Bic bank	2	500
Lukass	3	400
Alergo	4	600
Twój bank	5	300

Wykonać polecenia z zadania 2.

Współzależność cech jakościowych (tablice kontyngencji i asocjacji)

Zadanie 3 W kampanii prezydenckiej komitet wyborczy kandydata A zbierał informacje o poparciu społecznym dla tego kandydata. W losowo wybranej próbie otrzymano następujące informacje:

Płeć respondenta	Popiera	Nie popiera	Jeszcze nie wie	Suma
Kobieta	84	21	16	121
Mężczyzna	54	36	24	114
Suma	138	57	40	235=n

Zbadać, zależność pomiędzy płcią respondentów a poparciem kandydata

1.Badane zmienne to ......................................................................, które mają charakter .....................................

2. Dane zostały przedstawione w tablicy korelacyjnej, którą nazywamy

tablicą kon...................................... o wymiarach 2x......................................

3. Do oceny współzależności zmiennych (cech) o charakterze jakościowym przedstawionych ww. tablicy kontyngencji służą współczynniki ................................................................................

np. współczynnik zbieżności T-Czuprowa: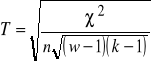

gdzie:
-to statystyka chi-kwadrat, w-liczba wierszy, k-liczba kolumn w tablicy kontyngencji.

, (
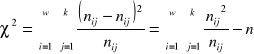
), gdzie:

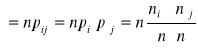
, n - całkowita liczba par obserwacji,
- liczebności empiryczne (z próby),

- liczebności teoretyczne tzn. są to liczebności, które wystąpiłyby gdyby zmienne X i Y były niezależne

84	.............
21	.............
16	............
54	66,94
36	27,65
24	19,40

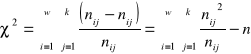
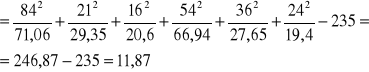
Jeżeli siła zależności pomiędzy zmiennymi X,Y wzrasta, to wartość statystyki
.....................

4. Współczynnika kontyngencji -współczynnik zbieżności T-Czuprowa:

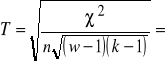
Wnioskujemy, że siła związku pomiędzy płcią respondentów a poparciem kandydata A jest ............................

Zadanie 3a (Zadanie domowe) Badaniem objęto 600 klientów sklepu, badając preferowany sposób płacenia (gotówka, karta płatnicza, inne). Jeżeli
=90 obliczyć współczynnik zbieżności T- Czuprowa.

Uwaga:

Tablica kontyngencji (korelacji) o wymiarach 2x2 nazywana jest tablicą asocjacji,

a współczynnik współzależności dla cech jakościowych przedstawionych w tablicy asocjacji nazywa się współczynnikiem
-Yula

Zadanie 3c Zbadano przyczyny rozwiązanie małżeństwa w 2002 roku z uwzględnieniem miejsca zamieszkania. W losowo wybranej próbie otrzymano:

Miejsce zamieszkania	Rozwiązanie małżeństwa		Razem
		Śmierć		Rozwód
Miasto	97 = a	38 = b	135 = (a+b)
Wieś	66 = c	7 = d	73 = (c+d)
Razem	163 = (a+c)	45 = (b+d)	208=n

Wykonać polecenia z zadania 3 Sprawdzić, czy istnieje związek statystyczny między sposobem rozwiązania małżeństwa, a miejscem zamieszkania?

1. Badane zmienne to ......................................................................, które mają charakter ....................................

2. Dane zostały przedstawione w tablicy korelacyjnej o wym. 2x2 nazywaną tablicą acocjacji

3. Do oceny współzależności zmiennych (cech) o charakterze jakościowym przedstawionych w tablicy asocjacji służą współczynniki asocjacji, np. współczynnik asocjacji
-Yula: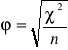
,

gdzie:
-to statystyka chi-kwadrat, n - liczebność próby

=
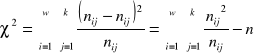
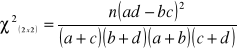
, gdy:

4. Zbadać siłę tego związku za pomocą współczynnika asocjacji
-Yula: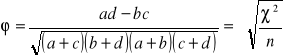
=..............

Siła tego związku jest ................................. , stąd wnioskujemy, że inne czynniki wpływają na sposób rozwiązania małżeństwa.

Funkcje regresji

1 Regresja to ............................. przyporządkowania jednej cechy (zmiennej zależnej) wartościom drugiej cechy (zmienna niezależna). Np.
, czyli zmienna X wpływa na zmienną Y.

zmienna X nazywamy zmienną nie............................ lub objaśnia..................................

zmienną Y nazywamy zmienną z............................ lub o..................................

2. Parametry funkcji regresji można oszacować metodą ................................................................, która polega na zminimalizowaniu kwadratów odchyleń wartości empirycznych
od wartości teoretycznych
(wyznaczonych z funkcji regresji).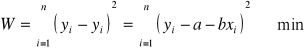

3. Regresja liniowa występuje wtedy, gdy ................................... zmianom zmiennej niezależnej ......towarzyszą ............................co do kierunku i siły zmiany zmiennej zależnej.......

Zadanie A Wyznaczyć i zinterpretować parametry liniowej funkcji regresji dla zadania 1a. W pewnej firmie produkcyjnej badano zależność zużycia głównego surowca od wielkości produkcji i otrzymano informacje zgodnie z poniższą tabelą.

Zużycie surowca w tonach (Xi)	1	2	3	4	5	6	7	8	9	10	11	12
Wielkość produkcji w tys. kg (Yi)	8	10	13	18	20	21	22	24	25	27	30	32

1. Wyznaczyć i zinterpretować parametry:

Parametr „a”

Parametr „b”

2. Wyznaczyć miary dobroci dopasowania funkcji regresji do danych empirycznych

R²

φ²

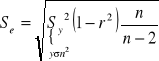
Ve

3. Obliczyć wielkość produkcji, gdy zużycie surowca będzie równe 15 ton (X=15)

4. Zakładając, że zależność pomiędzy badanymi zmiennymi nie jest liniowa, to dokonać interpretacji parametrów funkcji regresji krzywoliniowej, przyjmując wyniki z poprzedniego zadania (parametrów regresji liniowej).

Regresja funkcją hiperboliczną

Parametr „b” -..........................................

Parametr „a” - poziom ...............................(asymptota funkcji).

..............................................................................................................................................................................

..............................................................................................................................................................................

Regresja funkcją potęgową

Parametr „a” - ....................................... (nie interpretujemy).

Parametr „b” - współczynnik .................................

..............................................................................................................................................................................

..............................................................................................................................................................................

F3. Regresja funkcją wykładniczą

Parametr „a” - ....................................... (nie interpretujemy).

Parametr „b” - stopa .................................. (średni przyrost względny).

..............................................................................................................................................................................

..............................................................................................................................................................................

4. Dla każdej funkcji regresji z zadania 3 obliczyć miary dobroci dopasowania bezpośrednio z definicji.

F1. Regresja funkcją hiperboliczną	F2. Regresja funkcją potęgową	F3. Regresja funkcją wykładniczą	F3. Regresja funkcją LINIOWĄ
R^2 φ^2 Se Ve	R^2 φ^2 Se Ve	R^2 φ^2 Se Ve	R^2 φ^2 Se Ve

Funkcje regresji

Regresja liniowa występuje wtedy, gdy jednakowym zmianom zmiennej niezależnej towarzyszą jednakowe, co do kierunku i siły, zmiany zmiennej zależnej

stąd: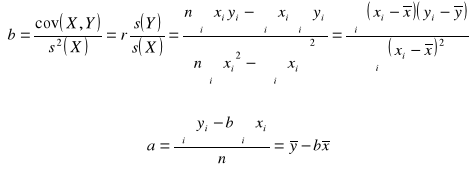

Parametr „a” - wyraz wolny.

Parametr „b” - współczynnik regresji

Int. „b”. Wzrost X o jednostkę powoduje wzrost (b>0)/spadek(b<0) wartości Y średnio o b jednostek.

Miary dopasowania funkcji regresji do danych

:
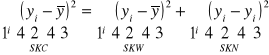
SKC=SKW+SKN

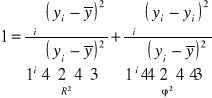
• φ² współczynnik zbieżności (indeterminancji)
  ,
  

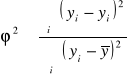
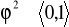
Int. φ²

- φ ² to udział zmienności niewyjaśnionej regresją w całkowitej zmienności Y (w ilu % Y nie zależy od X).

- w φ² 100% zmienność Y nie została wyjaśniona regresją liniową tzn. zmiennością X

• R² - współczynnik determinacji
  ,
  ,
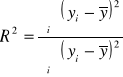
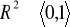
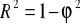
  (regresja liniowa)

Int. R²

- R ² to udział zmienności wyjaśnionej regresją w całkowitej zmienności Y (w ilu % Y zależy od X).

- w R² 100% zmienność Y została wyjaśniona regresją liniową tzn. zmiennością X .

• Se odchylenie standardowe reszt (średni błąd szacunku funkcji regresji)
  ,

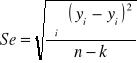
gdzie,
(reszta), k to liczba parametrów funkcji regresji (k=2).

Wartość liczbową odczytujemy z kalkulatora dla liniowej funkcji regresji jako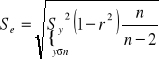

Int. Se: Rzeczywiste wartości zmiennej Y różnią się od oszacowanych na podstawie funkcji regresji liniowej średnio (+/-) o Se jednostek.

• Ve - Współczynnik zmienności przypadkowej (względny średni błąd szacunku)
  

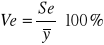
Int. Ve: Średni błąd szacunku stanowi Ve % przeciętnego poziomu Y.

Wniosek: natężenie wahań przypadkowych (losowych) jest ...........(małe/ umiarkowane/ średnie/ duże).

Regresja krzywoliniowa występuje wtedy, gdy jednakowym zmianom zmiennej niezależnej towarzyszą niejednakowe (różne) co do kierunku i siły zmiany zmiennej zależnej.

• Regresja funkcją hiperboliczną
  

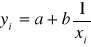
Parametr „b” - nie interpretujemy. Parametr „a” - poziom nasycenia (asymptota funkcji)

Jeżeli b>0, to Y maleje do nieprzekraczalnego-minimalnego poziomu a.

Jeżeli b<0, to Y rośnie do nieprzekraczalnego-maksymalnego poziomu a.

• Regresja funkcją potęgową
  

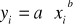
Parametr „b” - współczynnik elastyczności.

Int. „b”. Wzrost X o 1% powoduje wzrost (b>0)/spadek (b<0) wartości Y średnio o b%.

Parametr „a” - wyraz wolny (nie interpretujemy).

• Regresja funkcją wykładniczą
  

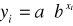
Parametr „b” - stopa przyrostu (średni przyrost względny).

Int. „b”. Wzrost X o jednostkę powoduje wzrost (b>1)/spadek (0<b<1) wartości Y średnio o (b-1)100%.

Parametr „a” - wyraz wolny (nie interpretujemy).

Stąd:

Powtórzenie

Korelacja to współzależność, ……………………….. lub współoddziaływanie dwóch cech, zmiennych.

Metody analizy współzależności to metody o…………………………….. i metody w………………………

1. Statystyczny opis współzależności może mieć formę:

a. t……………….., b. gr……………………, c. par……………………………..

2. Badając współzależność dwóch zmiennych (cech, zjawisk) o charakterze ilościowym korzystamy ze

• współczynnika korelacji liniowej ….................… który, bada kierunek oraz siłę związku korelacyjnego między dwiema cechami ilościowymi.

Badając współzależność dwóch zmiennych (cech, zjawisk) o charakterze porządkowym korzystamy ze

• współczynnika korelacji liniowej rang ……………………, który bada ocenę zgodności uporządkowań pomiędzy dwiema cechami o charakterze porządkowym.

• Badając współzależność dwóch zmiennych (cech, zjawisk) o charakterze jakościowym korzystamy ze

• współczynnika kontyngencji - współczynnika ……………….., który bada …………….. związku korelacyjnego pomiędzy dwiema cechami jakościowymi (lub jedną ilościową, a drugą jakościową lub dwiema cechami ilościowymi) wyrażonymi w tablicy ……………………. (tablicy korelacyjnej).

• współczynnika asocjacji -
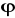
  -…………:, który bada ……………. związku korelacyjnego pomiędzy dwiema cechami jakościowymi (lub jedną ilościową, a drugą jakościową lub dwiema cechami ilościowymi) wyrażonymi w tablicy …………………. (tablicy kontyngencji o wymiarach 2x2)

• ze statystyki
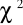
  , która pozwala przetestować, czy badane cechy (zmienne) są zależne statystycznie na pewnym poziomie istotności.

Jeżeli
=0, to zmienne X, Y są niezależne; gdy

, to zależność
pomiędzy zmiennymi X, Y.

Jeżeli
, to wtedy (możliwe, że
) zmniejsza się wymiar tablicy kontyngencji łącząc wiersze danych.

5. Jeżeli współczynnik korelacji liniowej Pearsona jest:

• r>0 to korelacja jest ……………….., zmiany obu zmiennych są w tym samym kierunku

• r<0 to korelacja jest ………………..., zmiany obu zmiennych są w przeciwnym kierunku

• r=0 to ………………………………między badanymi zmiennymi,

• r=±1 to związek funkcyjny jest …………….,

• im |r| dąży do 1, tym związek między badanymi zmiennymi jest ………………………

Statystyka ZiR Ćwiczenia 9-12 Analiza współzależności, regresja Strona 2 z 8

Analiza współzależności Strona 7

---