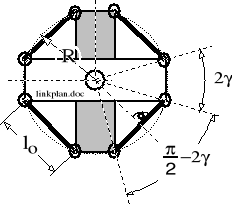
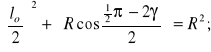8.5.3. Kinematyka sprzęgieł cięgłowych znakoprzemiennych.

We wstępie do (poprzedniego) paragrafu 8.5.2. powiedziano, że wychylne sprzęgła parzystocięgłowe mogą być zarówno znakoprzemienne jak i znakonieprzemienne. Sprzęgła cięgłowe, o liczbie cięgieł większej od trzech, nie są mechanizmami klasycznymi (są przesztywnione). Aby pracowały jako wychylne muszą więc zawierać elementy odkształcalne sprężyście. Jako statycznie niewyznaczalne podlegają one analizie przy uwzględnieniu dodatkowych równań równowagi sił powstających przy odkształceniu tych więzów sprężystych. Wprowadzenie dodatkowych równań statyki do wcześniej zastosowanych metod badania kinematyki zmienia kategorię badań w mechanice według poniższych definicji:

KINEMATYKA: Dział mechaniki ogólnej dotyczący geometrycznego opisu ruchu niezależnie od wywołujących ten ruch przyczyn.

KINETOSTATYKA: Analiza sił działających na człony mechanizmu podczas ich ruchu przy wykorzystaniu zasady d'Alemberta; to znaczy przez wprowadzenie sił bezwadności mas członów mechanizmu i zastosowanie statycznych warunków równowagi.

Kinetostatyka znakoprzemiennego sprzęgła czterocięgłowego

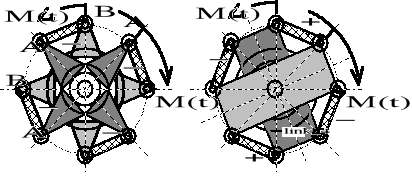
Rysunek 8.29. Schemat dwóch odmian sprzęgieł czterocięgłowych: znakonieprzemiennego (z lewej) i znakoprzemiennego (z prawej). Odmiany dotyczą wszystkich sprzęgieł parzystocięgłowych.

Szczegółowo zajmiemy się badaniem kinematyki sprzęgła (z prawej) czterocięgłowego znakoprzemiennego. Jest ono bowiem dość szeroko stosowane w budowie maszyn. Pojęcie kinematyki jest w tym przypadku dość osobliwe: w sensie klasycznym ściśle dotyczy ono jedynie przypadku pracy bez obciążenia roboczego, czyli dotyczy przypadku M(t) =0. Jedynie bowiem takim przypadku napięcia w cięgłach mają rozkład ściśle symetryczny (jak zaznaczono na rysunku): co do znaku i co do wartości. Niezależnie więc od rzeczywistych warunków sprzęgła w pojeździe lub maszynie roboczej znajomość tak pojmowanego, wewnętrznego tętna kinematycznego determinuje wymuszenia wibracyjne w układzie napędowym.

Wartość techniczna analizy kinetostatyki sprzęgła jest więc niekwestionowana: przynosi wynik kinematyczny w określonym sensie (według powyższego komentarza).

Sprzęgło będziemy badać w sposób mieszany: stosując zarówno metodę geometrii przestrzennej jak i metodę bilansu wewnętrznych sił uogólnionych.

Zastosowanie geometrii przestrzennej wymaga przyjęcia trzech układów współrzędnych: OA,XYZ - nieruchomego (niewirującego) układu odniesienia związanego z wałem aktywnym, układu OB,X',Y',Z' - niewirującego układu translacyjnego względem układu OA,XYZ o wielkość wektora
, oraz układu niewirującego OB,X,Y,Z - związanego z wałem biernym, na który narzucono dodatkowo wychylność.

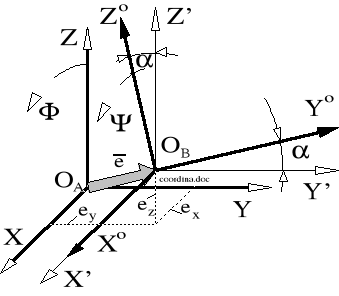
Rysunek 8.30. Układy współrzędnych do badania kinetostatyki sprzęgła czterocięgłowego znakoprzemiennego.

transformacje współrzędnych

transformacja pierwsza: przesunięcie równoległe

transformacja druga: obrót o kąt alfa

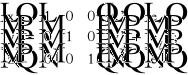
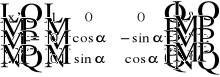
(8.105)

Stosowane w technice transmisji momentu trakcyjnego sprzęgła czterocięgłowe mają postać pokazaną schematycznie na rysunku 8.31 przy czym ogólnie 0.

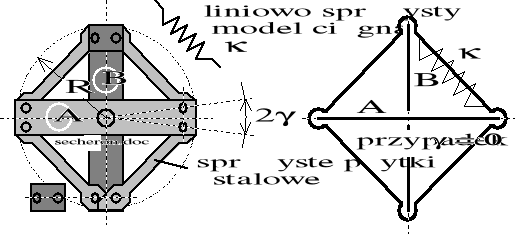
Rysunek 8.31. Schematyczna postać sprzęgła czterocięgłowego.

Najczęściej jednak stosowane jest wykonanie sprzęgła z tulejami metalowo - gumowymi osadzonymi w gniazdach łączników korbowodowych. Wykonanie takie przykładowo zilustrowano rysunkiem 8.32.

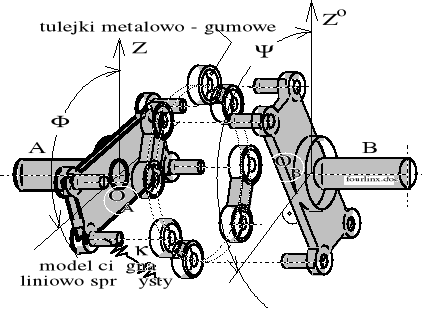
Rysunek 8.32. Schemat techniczny popularnej odmiany sprzęgła czterocięgłowego.

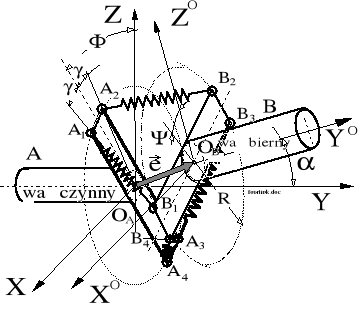
Rysunek 8.33. Schemat sprzęgła czterocięgłowego przyjęty do analizy jego kinetostatyki. Układ obejmuje przypadki techniczne według rysunków 8.31 i 8.32.

Współrzędne położenia punktów A1 i A2 w układzie OAXYZ:

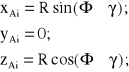
(8.106)

(i=1,2); znak górny dla i=1.

Współrzędne położenia punktów B1 i B2 w układzie OBXYZ;

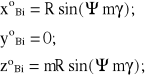
(8.107)

Bezpośredna transformacja układów: OBXYZ OAXYZ , wynikająca z wykorzystania zależności (8.105) ma następującą postać:

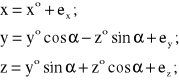
(8.108)

Na podstawie (8.108) współrzędne położenia punktów B1 i B2 w układzie OAXYZ wyraża się następująco:

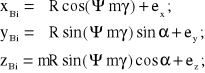
(8.109)

Odległość punktów Ai-Bi w przestrzeni jest określona przez związek:

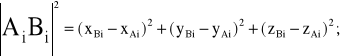
(8.110)

Po podzieleniu stronami przez R2, poszczególne wyrazy (8.110) przybierają następującą postać:

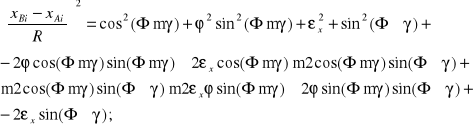
(8.111a)

gdzie (i w dalszym ciągu) oznaczono:

(8.111b)

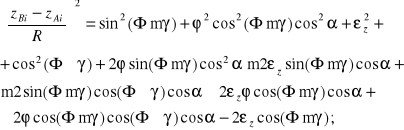
(8.111c)

Podobne związki można otrzymać dla punktów 3 i 4 sprzęgła, gdzie w miejsce należy wstawić kąt +.

Powstaje w ten sposób 6 wyrażeń typu (8.111), dla łączników ponumerowanych jako 1 i 2, oraz 6 wyrażeń dla łączników o numeracji 3 i 4.

Położenie względne elementów A i B sprzęgła w przestrzeni jest określone przez równowagę sił w cięgłach. Siły te liniowo zależne są od wydłużeń cięgieł lj (j=1,2,3,4); Należy więc wyrazić te wydłużenia w funkcji wielkości:

,,,x,y,z,;

Podstawowe związki geometryczne w sprzęgle.

Rysunek 8.34. Geometria sprzęgła nieodkształconego

Do powyższego równania podstawimy elementarną zależność trygonometryczną:

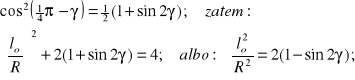
(8.112)

Wydłużenia cięgieł (przestrzenne):

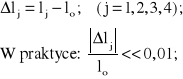
W wyrażeniach przybliżonych zachowamy lj w pierwszej potędze; wyższe potęgi można w obliczeniach technicznych odrzucić.

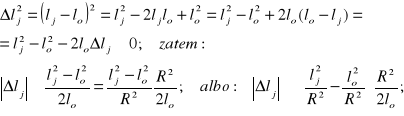
(8.113)

Pierwszy wyraz w nawiasie powyższego wzoru (8.113) stanowi sumę trzech wyrażeń (8.111);

Drugi wyraz w nawiasie powyższego wzoru opisuje wyrażenie (8.112);

Za nawiasem znajduje się wielkość stała, charakteryzująca geometrię sprzęgła.

Na mocy (8.113) możemy więc (po dość żmudnych przekształceniach formalnych) napisać:

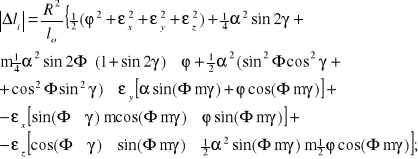
(8.114)

W ten sposób wydłużenia cięgieł, wyrażone w pierwszej potędze, możemy wyznaczyć bezpośrednio posługując się kwadratową formą wyrażeń (8.111).

Teraz rozważymy cztery techniczne przypadki pracy sprzęgła.

Przypadek pierwszy: Przy quasistatycznym obracaniu się wyśrodkowanego (e=0) sprzęgła załamanego pod kątem , bez obciążenia roboczego, wydłużenia wszystkich cięgieł zawsze będą jednakowe i dodatnie.

Przypadek drugi: Przy współosiowej pracy wałów sprzęgła obciążonego momentem roboczym znaki wydłużeń w sąsiadujących cięgłach będą jednakowe co do wartości bezwzględnej lecz różnoimienne. Wydłużenia cięgieł przeciwległych będą jednakowe co do wartości i jednoimienne.

Przypadek trzeci: Przy siłą narzuconej niewspółosiowości odsuwnej sprzęgła nieobciążonego momentem roboczym, wartości bezwzględne wydłużeń w cięgłach przeciwległych będą jednakowe lecz różnoimienne.

Przypadek czwarty: Przy narzuconej (wyłącznie) niewspółosiowości wysuwnej sprzęgła o niezałamanych osiach wałów, wydłużenia wszystkich cięgieł będą dodatnie i jednakowe.

Ogólnie więc superponujące się wydłużenia cięgieł mogą pochodzić od:

- niewspółosiowości wychylnej l*j;

- momentu roboczego lj;

- siłą narzuconej niewspółosiowości odsuwnej;

- siłą narzuconej niewspółosiowości wysuwnej.

Pod względem technicznym najbardziej interesują nas pierwsze dwa przypadki. Obracające się sprzęgło, pracujące według przypadku pierwszego, doznając wydłużeń cięgieł l*i; (i=1,2); może doznawać względnych kątowych zaburzeń *=*(,) kąta obrotu wału B względem wału A.

Dla przypadku pierwszego (dla cięgieł sąsiadujących i=1,2) możemy napisać:

Zatem na mocy (8.114), biorąc powyższą zależność pod uwagę, możemy napisać:

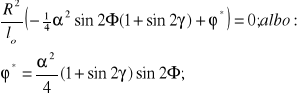
(8.115)

gdzie: *=-; kąt zaburzenia przemieszczenia kątowego wałów sprzęgła obracającego się bez obciążenia roboczego. Jest to strukturalna funkcja położenia sprzęgła.

Dla przypadku drugiego możemy wziąć pod uwagę zarówno cięgła przeciwległe (j=1,2,3,4) jak też cięgła sąsiadujące. Spełnione są bowiem obydwie zależności:

Na mocy powyższego możemy napisać natępujący warunek, który w omawianym przypadku tożsamościowo spełnia się na mocy samych założeń tego przypadku:

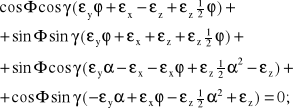
(8.116)

Związek ten musi obowiązywać także w innych przypadkach. W przypadku obciążenia momentem w warunkach niewspółosiowości małe wydłużenia cięgieł parzystych będą jednakowe i równe skróceniom cięgieł nieparzystych jeśli nie zostanie siłą narzucona superpozycyjna niewspółówsiowość odsuwna i wysuwna. Sprzęgło więc samoczynnie środkuje się wzajemnie. Biorąc pod uwagę (8.116), na mocy (8.114) możemy napisać dla ogólnego przypadku technicznego

My0; 0;

(8.117)

gdzie: =*+;

* - kąt skręcenia kinematycznego (strukturalnego); *=*(,)

- kąt roboczego skręcenia sprężystego; =My/;

- sztywność skrętna sprzęgła.

Identyczny jak (8.117) związek możemy otrzymać analizując wydłużenia cięgieł 3 i 4. Oznacza to, że quasistatycznemu obrotowi sprzęgła nie towarzyszą względne przemieszczenia poprzeczne oraz podłużne. Sprzęgło jest poprzecznie równobieżne pod względem kinematycznym. Oznacza to tylko tyle, że wał B nie doznaje zaburzenia niewspółosiowości wywołanej pracą cięgieł sprężystych. Nie oznacza to jednak, że nie mogą pojawić się sprężyste przemieszczenia poprzeczne wałów wynikające ze statyki elementarnej KAŻDEGO sprzęgła wychylnego.

Sprzęgło czterocięgłowe nie generuje kinematycznych zaburzeń strukturalnych poprzecznej niewspółosiowości wałów.

Dwa sprzęgła czterocięgłowe lub krzyżakowe pracujące w układzie szeregowym

Kąt statycznego skręcenia środkowego odcinka traktujemy jako stały:

gdzie M - moment roboczy (trakcyjny); - sztywność skrętna wału.

Mamy dwa podstawowe warianty montażowe:

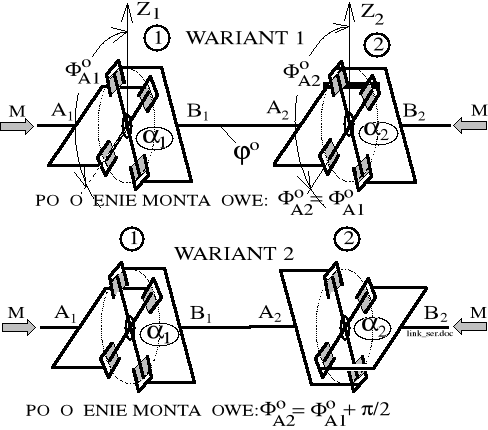
Rysunek 8.35. Wariantowe położenia montażowe zespołu dwóch sprzęgieł.

Zaburzenia ruchu układu pochodzą od funkcji położenia sprzęgła *=*():

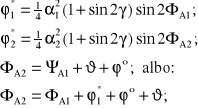
gdzie: - kąt montażowy względnego osadzenia sprzęgieł w wale przegubowym.

Dobrze jest, gdy:

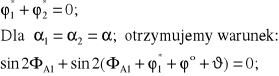
Pomijając wielkości małe
otrzymujemy spełnienie warunku dla

Wtedy
czyli kąt wypadkowego zaburzenia położenia wału B2 jest równy zeru.

Ramię wału czynnego w sprzęgle pierwszym, w stosunku do ramienia wału czynnego w sprzęgle drugim, powinno być obrócone o 90. Inaczej mówiąc, widełki środkowego odcinka wału przegubowego powinny być zmontowane we wspólnej płaszczyźnie z osią tego ocinka.

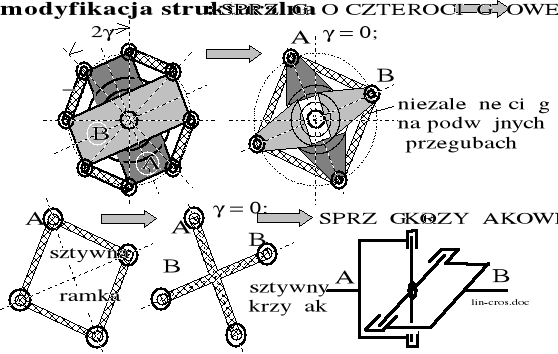
Rysunek 8.36. Modyfikacja strukturalna sprzęgła czterocięgłowego do postaci krzyżakowej.

Konkluzje do p. 8.5.3:

Sprzęgło czterocięgłowe więzy sprężyste zawierać musi; sprzęgło krzyżakowe zawierać takie więzy może.

Wszystkie sztywne struktury o wartości kąta = 0, są całkowicie równoważne kinematycznie.

Literatura źródłowa do p. 8.5.3:

[1] Madej J.: Mechanika napędu pojazdów szynowych... PWN Warszawa 1983

230

---