SPRAWOZDANIE Z LABORATORIUM

METOD NUMERYCZNYCH

Ćwiczenie 3

Interpolacja i aproksymacja

Wydział: EEIA

Rok akademicki: 2012/2013

semestr IV

Grupa: 4C5

Dzień: czwartek godz. 14¹⁵-16⁰⁰

Jarosław Król 163543

Celem ćwiczenia było praktyczne zaznajomienie się z podstawowymi aspektami interpolacji wielomianowej, interpolacji funkcjami sklejanymi i aproksymacji średniokwadratowej.

1. M-funkcja wykonująca aproksymację funkcji i badająca błędy w zależności od stopnia wielomianu przybliżającego:

function [ w,y2,er,m ] = aperr( x,y,n )

x=[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1];

y=[-0.3684,-0.2553,-0.1245,0.0187,0.1854,0.3522,0.5451,0.7822,1.0244,1.2860,1.5596];

n=7;

kolory=jet(n);

subplot(1,2,1)

plot(x,y,'r--')

for i=1:n

w=polyfit(x,y,1+i); %współczynniki wielomianu

y2=polyval(w,x); %rozwiązanie wielomianu

hold on

subplot(1,2,1)

plot(x,y2,'Color',kolory(i,:))

er=y-y2; %błąd

subplot(1,2,2)

plot(x,er,'Color',kolory(i,:))

m=max(er) %błąd maksymalny

end

hold off

end

Wykresy: funkcji przybliżających i błędów:

2.

3.

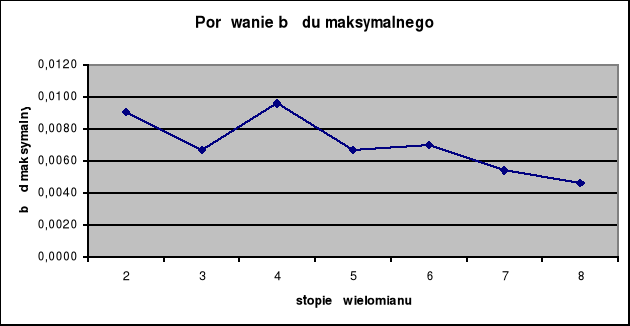
Porównanie błędu maksymalnego poszczególnych wariantów aproksymacji
stopień wielomianu aproksymującego	błąd maksymalny
2	0,0091
3	0,0067
4	0,0096
5	0,0067
6	0,0070
7	0,0054
8	0,0046

4. M-funkcja znajdująca wielomian interpolacyjny za pomocą rodziny trójkątnej:

function [P]=trr(x,y)

x=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1];

y=[-0.3684 -0.2553 -0.1245 0.0187 0.1854 0.3522 0.5451 0.7822 1.0244 1.2860 1.5596];

for i=1:length(x) %pierwsza kolumna macierzy

B(i,1)=1; %która zawiera same ,,1''

end

for i=1:length(x) %druga kolumna macierzy

B(i,2)=x(i)-x(1);

end

for t=3:length(x) %kolumny macierzy od trzeciej do ostatniej

for i=1:length(x)

B(i,t)= (x(i)-x(t-1))*B(i,t-1);

end

end

C=inv(B)*y' %obliczenie wektora współczynników

%wyznaczanie wielomianów fi

a=sym('x');

fi2=a-x(1,1);

fi=fi2;

for q=2:length(x)-1

fi(1,q)=(a-x(1,q))*fi(1,q-1);

end

FI=[1 fi];

P=FI*C %wielomian

end

5.Funkcja obliczająca współczynniki aproksymacji średniokwadratowej funkcją f(x)=a*exp(x)+b

function [ B ] = apro( x,y )

x=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1];

y=[-0.3684 -0.2553 -0.1245 0.0187 0.1854 0.3522 0.5451 0.7822 1.0244 1.2860 1.5596];

A=zeros(2,2); %gramian

C=zeros(2,1);

n=length(x);

A(1,1)=n;

p=0;

for i=1:n

z=exp(x(i));

p=p+z;

end

A(1,2)=p;

A(2,1)=p;

h=0;

for i=1:n

z=exp(x(i));

q=dot(z,z); %iloczyny skalarne

h=h+q;

end

A(2,2)=h;

s=0;

for i=1:n

ar=y(i);

s=s+ar;

end

C(1,1)=s;

io=0;

for i=1:n

op=exp(x(i));

oq=dot(op,y(i));

io=io+oq;

end

C(2,1)=io;

B=inv(A)*C; %szukane współczyyniki

b=B(1,1);

a=B(2,1);

y1=a*exp(x)+b;

hold on

plot(x,y1) %wykres funkcji aproksymującej

%porównanie z aproksymowaniem wielomianem drugiego stopnia

w=polyfit(x,y,2);%współczynniki wielomianu

y2=polyval(w,x); %rozwiązanie wielomianu

plot(x,y2,'r')

y12=y1-y;

y22=y2-y;

plot(x,y12)

plot(x,y22,'r')

end

Wykres przedstawiający aproksymację funkcją f(x)=a*exp(x)+b i wielomianem drugiego stopnia.

Wykresy błędów aproksymacji funkcji:

6. Interpolacja funkcji y=e^-x2 na przedziale [-5,3] metodą interpolacji wielomianami różnych stopni oraz interpolację funkcjami sklejanymi (wielomianami 3 stopnia).

function [G] = interpp( x1 )

%Interpolacja funckji y=e^-x^2 różnymi metodami

%1. Interpolacja wielomianami różnych stopni tej funkcji naprzedziale [-5,3]

% do wykresu funkcji

x1=[-5:3];

y1=exp(-x1.^2);

subplot(2,1,1)

plot(x1,y1)

hold on

for N=2:10

x=[-5:8/N:3];

y=exp(-x.^2);

w=polyfit(x,y,N);%współczynniki wielomianu interpolacyjnego

y2=polyval(w,x1);

subplot(2,1,1)

plot(x1,y2,'r')

hold on

subplot(2,1,2)

blad=y1-y2;

plot(x1,blad,'r')

hold on

end

%interpolacja funkcjami sklejanymi

for N=2:10

x=[-5:8/N:3];

y=exp(-x.^2);

xi=[-5:3];

yi=interp1(x,y,xi,'spline'); %interpolacja funkcjami sklejanymi

subplot(2,1,1)

plot(xi,yi,'g')

blad1=y1-yi

subplot(2,1,2)

plot(x1,blad1,'g')

hold on

end

end

Wykresy funkcji dla węzłów równoodległych od 3:11

Wykresy czerwone dotyczą interpolacji wielomianowej, a wykresy zielone dotyczą interpolacji funkcjami sklejanymi.

Jak widać interpolacja z węzłami równoodległymi daje dobre przybliżenie w środku przedziału, natomiast na krańcach występują znaczne odchylenia.

Zestawienie normy maksymalnej:

Największy błąd występuje gdy ilość węzłów jest równa 3

N+1	Błąd max interpolacji wielomianowej	Błąd max interpolacji funkcjami sklejanymi
3	0.6551	0.6551
4	0.2718	0.2718
5	0.5689	0.5747
6	0.4840	0.2245
7	0.3368	0.1687
8	0.1034	0.1304
9	3.2045e-015	2.4395e-018
10	0.0502	0.0496
11	0.0393	0.0189

.

---