WYDZIAŁ BUDOWY MASZYN 10.05.2001r.
STUDIA INŻYNIERSKIE
ROK AKADEMICKI 2000/2001
Czwartek godz. 1215
Laboratorium
Metrologii Wielkości Geometrycznych
Temat: Pomiary pośrednie.
Wykonali:
Marek Czyba
Michał Żydaczewski
Dawid Gołchowski
Marcin Hyla
![]()
Wprowadzenie.
Pomiar pośredni - to metoda pomiarowa, która umożliwia pomiar wielkości pośrednio, z pomiarów bezpośrednich innych wielkości związanych odpowiednio z wielkością mierzoną.
Przebieg ćwiczenia.
1. Pomiar promienia łuku przez pomiar strzałki i cięciwy.
Pomiaru tego dokonujemy przy pomocy mikroskopu warsztatowego małego (MWM). Rzeczywistym celem pomiaru jest promień łuku R, a my zmierzymy strzałkę s i odpowiadającą jej cięciwę c bezpośrednio, a następnie pośrednio przez wprowadzenie wzoru wyliczymy promień łuku R. Mierzony promień R jest zatem funkcją strzałki i cięciwy łuku.
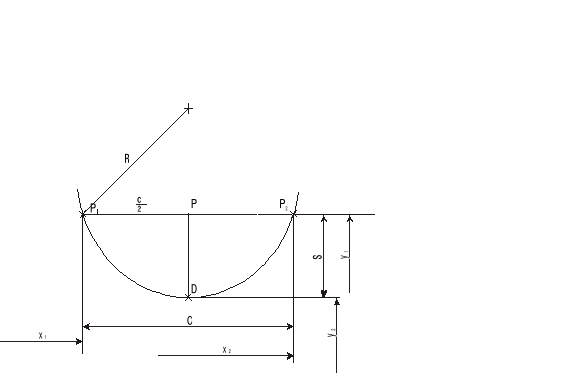
gdzie:
R - promień łuku;
c - cięciwa;
s - strzałka.
Przebieg ćwiczenia:
Głowicą goniometryczną MWM obieramy jeden punkt P1 na łuku i odczytujemy jego współrzędne:
P1 (0,000 ; 7,470)
Następnie przy pomocy pokrętła śruby mikrometrycznej, umieszczonej w MWM, (w osi OX) przesuwamy się do przeciwległego punktu P2 leżącego na łuku i odczytujemy jego współrzędne:
P2 (13,153 ; 7,470)
Liczymy średnią arytmetyczną tych dwóch wskazań (w osi OX), aby wyznaczyć interesującą nas współrzędną środka punktu P (x3 ; y3).
![]()
stąd
P (6,577 ; 7,470)
Następnie wzdłuż osi OX przesuwamy się do tej współrzędnej i już prostopadle do osi OX przesuwam się do punktu D (x ;y) na łuku odczytując następnie jego współrzędne:
D ( 6,577 ; 5,592)
Z powyższych wskazań obliczamy:
![]()
![]()
Następnie wyprowadzam (z trójkąta OP1P) wzór na promień:
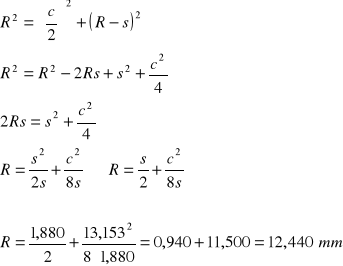
jeżeli y = f(x1... xn) to niepewność
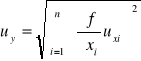
ponieważ R = f(c,s) to:
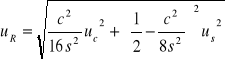
![]()
![]()
![]()
![]()
R = 12,440 ±0,007 mm
2. Pomiar promienia łuku wałeczkami.
Jest to pomiar pośredni, wielkościami mierzonymi bezpośrednio są:
wymiar M;
średnica wałeczków d;
Promień łuku R oblicza się ze przy pomocy tych dwóch wielkości.
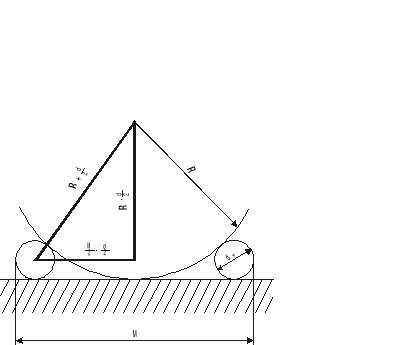
gdzie:
R - promień łuku;
d - średnica wałeczków;
M - wymiar mierzony.
Przebieg ćwiczenia:
Najpierw odczytujemy średnicę pierwszej pary wałeczków d1 = 20,002 mm, to samo robimy dla drugiej pary d2 = 29,995.
Pierwszy pomiar przeprowadzamy dla wałeczków d1
M1 = 115,955 mm
Później to samo robimy dla wałeczków d2
M2 = 147,539 mm
Następnie korzystając z trójkąta AOB wyprowadzam ogólny wzór na promień łuku R:
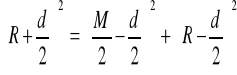
![]()
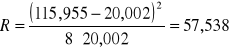
jeżeli y = f(x1... xn) to niepewność:
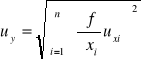
ponieważ R = f(M,d) to:
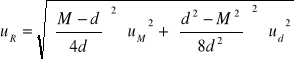
![]()
![]()
dla pierwszej pary wałeczków:
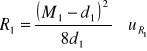
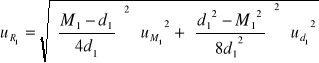
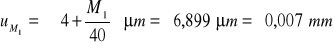
![]()
![]()
dla drugiej pary wałeczków:
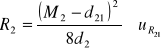
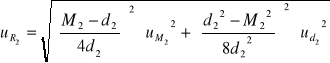
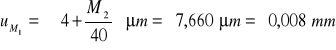
![]()
![]()
Ten wynik jest bardziej wiarygodny, gdyż dla tych wałeczków mniejsza jest niepewność pomiaru promienia R. Więc ten wynik będziemy brali pod uwagę.
Pomiar kąta stożka zewnętrznego przy użyciu wałeczków pomiarowych.
Jest to pomiar metodą pośrednią. Oprócz wałeczków pomiarowych do pomiaru używa się płytek wzorcowych i mikrometru, którym mierzy się długości pomiarowe M1 i M2.
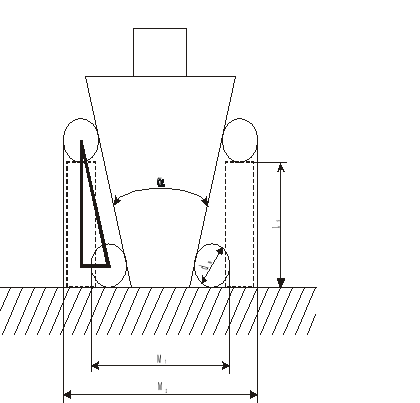
gdzie:
α - mierzony kąt stożka;
ls - długość stosu płytek wzorcowych;
d - średnica wałeczków.
Przebieg ćwiczenia.
Najpierw mierzymy średnicę wałeczków pomiarowych d:
d = 6,349 mm
Następnie dokonujemy pomiaru długości M1, gdy wałeczki znajdują się na płycie:
M1 = 43,565 mm
Kolejny pomiar długości M2 przeprowadzamy, gdy wałeczki pomiarowe umieścimy na stosie płytek wzorcowych o wysokości Ls = 25 mm:
M2 = 48,250 mm
Kąt stożka α można wyznaczyć z zależności obowiązującej w trójkącie pokazanym na szkicu. W celu przeliczenia wyniku na minuty kątowe należy go pomnożyć przez 3,44 (1mrad = 3,44'):
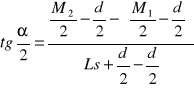
![]()
ostatecznie:
![]()
![]()
Mierzony kąt α stożka zewnętrznego jest więc funkcją trzech wymiarów:
(M1- M2), (d-d) oraz Ls
![]()
w rzeczywistości nie interesują nas wielkości M1, M1 oraz d - ważne jest że w różnych położeniach kątowych wymiary wałeczka mogą się różnić. Niepewność Mα pomiaru kąta α stożka oblicz się więc wg wzoru:
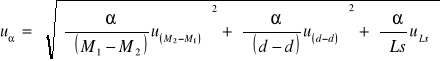
ostatecznie:
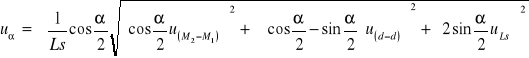
Z zależności tej wynika, że niepewność pomiaru zależy głównie od długości stosu płytek wzorcowych Ls. Im większe Ls tym mniejsze uα.
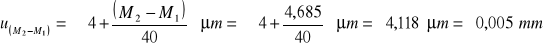
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
03. rysunek wykonawczy, Politechnika Lubelska, Studia, Studia, Sprawka 5 semestr, technologia maszyn
Technologia Maszyn CAD CAM
Proces technologiczny do podyktowania, TM - Technologia Maszyn, O procesie technologicznym
KARTA INSTRUKCYJNA OBROBKI2, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Se
Str.4 - Karta technologicza zbiorcza, Politechnika Lubelska, Studia, Studia, organizacja produkcji,
TM10, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, Wydział Mechaniczn
Karty technologiczne, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, te
Karta operacyjna 80, Politechnika Lubelska, Studia, Studia, wszystkie, Uczelnia, Technologia Maszyn,
czystakartainstrukcyjnaobrobki, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL,
technologia maszyn
Karta operacyjna50 gotowa, Politechnika Lubelska, Studia, Studia, wszystkie, Uczelnia, Technologia M
Str.10 - Operacja 50, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, te
stale stopowe-referat, Technologia maszyn, 05.Metaloznastwo - Metalurgia
Str.13 - Operacja 80, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, te
05 h zaokrąglanie, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, Wydzi
15. Karta kontrolna, Politechnika Lubelska, Studia, Studia, Sprawka 5 semestr, technologia maszyn tu
więcej podobnych podstron