Model ekonometryczny
:
Model ma na celu wyjaśnienie kształtowania się wielkości emisji dwutlenku siarki w Europie (przedstawionego w setkach ton rocznie) w zależności od wielkości emisji trafiającej do Polski (przedstawionego w setkach ton rocznie).
Do tego celu posłużę się Testem mnożnika Lagrange'a, który rozstrzyga o istnieniu bądź nieistnieniu autokorelacji I rzędu.
Dane do budowy modelu zaczerpnęłam z tablic geograficznych z roku 1998 , model jest oparty na 40 obserwacjach .
Działania wykonałam za pomocą programu Microsoft Excel
Szacuję model podstawowy: y=a+bx+ε
y - zmienna objaśniana - wielkość emisji dwutlenku siarki w Europie (przedstawionego w setkach ton rocznie)
x - zmienna objaśniająca- wielkości emisji trafiającej do Polski (przedstawiona w setkach ton rocznie)
a,b - parametry modelu
ε - składnik losowy
e - reszty modelu podstawowego(e=y- ŷ)
n - liczba obserwacji
n=40
Tabela 1. W tabeli umieszczam wartości zmiennych i działania z nimi związane, które potrzebne są do dalszych obliczeń.
t |
y |
x |
y2 |
x2 |
1 |
2,0000 |
203,0000 |
4,0000 |
41209,0000 |
2 |
16,0000 |
253,0000 |
256,0000 |
64009,0000 |
3 |
12,0000 |
887,0000 |
144,0000 |
786769,0000 |
4 |
35,0000 |
982,0000 |
1225,0000 |
964324,0000 |
5 |
35,0000 |
1534,0000 |
1225,0000 |
2353156,0000 |
6 |
35,0000 |
4264,0000 |
1225,0000 |
18181696,0000 |
7 |
6,0000 |
188,0000 |
36,0000 |
35344,0000 |
8 |
578,0000 |
4113,0000 |
334084,0000 |
16916769,0000 |
9 |
20,0000 |
548,0000 |
400,0000 |
300304,0000 |
10 |
4,0000 |
393,0000 |
16,0000 |
154449,0000 |
11 |
3,0000 |
321,0000 |
9,0000 |
103041,0000 |
12 |
27,0000 |
3313,0000 |
729,0000 |
10975969,0000 |
13 |
4,0000 |
1472,0000 |
16,0000 |
2166784,0000 |
14 |
3,0000 |
5850,0000 |
9,0000 |
34222500,0000 |
15 |
7,0000 |
492,0000 |
49,0000 |
242064,0000 |
16 |
1,0000 |
59,0000 |
1,0000 |
3481,0000 |
17 |
0,0000 |
602,0000 |
0,0000 |
362404,0000 |
18 |
48,0000 |
1317,0000 |
2304,0000 |
1734489,0000 |
19 |
26,0000 |
374,0000 |
676,0000 |
139876,0000 |
20 |
4,0000 |
133,0000 |
16,0000 |
17689,0000 |
21 |
4,0000 |
281,0000 |
16,0000 |
78961,0000 |
22 |
4,0000 |
181,0000 |
16,0000 |
32761,0000 |
23 |
1132,0000 |
11188,0000 |
1281424,0000 |
125171344,0000 |
24 |
1,0000 |
124,0000 |
1,0000 |
15376,0000 |
25 |
3026,0000 |
8312,0000 |
9156676,0000 |
69089344,0000 |
26 |
0,0000 |
409,0000 |
0,0000 |
167281,0000 |
27 |
50,0000 |
8294,0000 |
2500,0000 |
68790436,0000 |
28 |
104,0000 |
2686,0000 |
10816,0000 |
7214596,0000 |
29 |
137,0000 |
821,0000 |
18769,0000 |
674041,0000 |
30 |
32,0000 |
521,0000 |
1024,0000 |
271441,0000 |
31 |
7,0000 |
313,0000 |
49,0000 |
97969,0000 |
32 |
2,0000 |
126,0000 |
4,0000 |
15876,0000 |
33 |
0,0000 |
1009,0000 |
0,0000 |
1018081,0000 |
34 |
131,0000 |
5364,0000 |
17161,0000 |
28772496,0000 |
35 |
261,0000 |
2350,0000 |
68121,0000 |
5522500,0000 |
36 |
38,0000 |
9057,0000 |
1444,0000 |
82029249,0000 |
37 |
43,0000 |
4234,0000 |
1849,0000 |
17926756,0000 |
38 |
13,0000 |
8019,0000 |
169,0000 |
64304361,0000 |
39 |
12,0000 |
239,0000 |
144,0000 |
57121,0000 |
40 |
18,0000 |
1602,0000 |
324,0000 |
2566404,0000 |
SUMA |
5881,0000 |
92428,0000 |
10902931,0000 |
563582720,0000 |
Ciąg dalszy tabeli
t |
xy |
ŷ |
e |
e2 |
1 |
406,0000 |
-32,8336 |
34,8336 |
1213,3809 |
2 |
4048,0000 |
-28,5669 |
44,5669 |
1986,2099 |
3 |
10644,0000 |
25,5349 |
-13,5349 |
183,1931 |
4 |
34370,0000 |
33,6416 |
1,3584 |
1,8452 |
5 |
53690,0000 |
80,7460 |
-45,7460 |
2092,6991 |
6 |
149240,0000 |
313,7080 |
-278,7080 |
77678,1702 |
7 |
1128,0000 |
-34,1136 |
40,1136 |
1609,1032 |
8 |
2377314,0000 |
300,8226 |
277,1774 |
76827,3149 |
9 |
10960,0000 |
-3,3934 |
23,3934 |
547,2495 |
10 |
1572,0000 |
-16,6201 |
20,6201 |
425,1904 |
11 |
963,0000 |
-22,7642 |
25,7642 |
663,7939 |
12 |
89451,0000 |
232,5553 |
-205,5553 |
42252,9968 |
13 |
5888,0000 |
75,4553 |
-71,4553 |
5105,8622 |
14 |
17550,0000 |
449,0479 |
-446,0479 |
198958,7036 |
15 |
3444,0000 |
-8,1721 |
15,1721 |
230,1918 |
16 |
59,0000 |
-45,1217 |
46,1217 |
2127,2134 |
17 |
0,0000 |
1,2147 |
-1,2147 |
1,4754 |
18 |
63216,0000 |
62,2285 |
-14,2285 |
202,4512 |
19 |
9724,0000 |
-18,2415 |
44,2415 |
1957,3096 |
20 |
532,0000 |
-38,8070 |
42,8070 |
1832,4395 |
21 |
1124,0000 |
-26,1776 |
30,1776 |
910,6852 |
22 |
724,0000 |
-34,7110 |
38,7110 |
1498,5390 |
23 |
12664816,0000 |
904,5611 |
227,4389 |
51728,4381 |
24 |
124,0000 |
-39,5750 |
40,5750 |
1646,3314 |
25 |
25152112,0000 |
659,1403 |
2366,8597 |
5602024,6031 |
26 |
0,0000 |
-15,2548 |
15,2548 |
232,7089 |
27 |
414700,0000 |
657,6043 |
-607,6043 |
369183,0300 |
28 |
279344,0000 |
179,0509 |
-75,0509 |
5632,6340 |
29 |
112477,0000 |
19,9028 |
117,0972 |
13711,7456 |
30 |
16672,0000 |
-5,6974 |
37,6974 |
1421,0927 |
31 |
2191,0000 |
-23,4469 |
30,4469 |
927,0119 |
32 |
252,0000 |
-39,4043 |
41,4043 |
1714,3195 |
33 |
0,0000 |
35,9456 |
-35,9456 |
1292,0892 |
34 |
702684,0000 |
407,5755 |
-276,5755 |
76494,0148 |
35 |
613350,0000 |
150,3786 |
110,6214 |
12237,0877 |
36 |
344166,0000 |
722,7142 |
-684,7142 |
468833,5789 |
37 |
182062,0000 |
311,1480 |
-268,1480 |
71903,3582 |
38 |
104247,0000 |
634,1375 |
-621,1375 |
385811,7537 |
39 |
2868,0000 |
-29,7616 |
41,7616 |
1744,0305 |
40 |
28836,0000 |
86,5487 |
-68,5487 |
4698,9305 |
SUMA |
43456948,0000 |
5881,0000 |
0,0000 |
7489542,7765 |
Ponieważ suma reszt równa się zero , to model jest zbudowany poprawnie
Posługując się danymi z tabeli obliczam macierze potrzebne do oszacowania modelu:
Wyznaczam macierz XTX
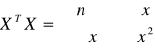
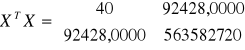
Wyznaczam macierz (XTX) -1
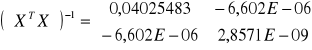
Wyznaczam macierz XTY
Wyznaczam parametry a i b modelu podstawowego
A-wektor parametrów modelu
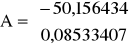
a=-50,156434
b=0,08533407
Stosując metodę najmniejszych kwadratów do oszacowania parametrów otrzymałam następujący model ekonometryczny :
Model oszacowany : ŷ=a+bx+ε
ŷ=-50,156434+0,08533407x
Wniosek: Jeżeli emisja dwutlenku siarki w Europie wzrośnie o 100 ton rocznie to zanieczyszczenie dwutlenkiem siarki w Polsce wzrośnie o 0,08533407 setek ton (przy innych niezmiennych czynnikach).
Szacuję model pomocniczy: et=a1+b1x+c1et-1+ηt
et - zmienna objaśniana ( wartości reszt modelu podstawowego bez jednej obserwacji)
x, et-1- zmienne objaśniające
a1, b1, c1 - parametry modelu pomocniczego
ηt- składnik losowy
r- reszty modelu pomocniczego(r = et - êt)
N- liczba obserwacji modelu pomocniczego
N=39
Tabela 2.1. W tabeli umieszczam wartości zmiennych, potrzebne do dalszych obliczeń
t |
et |
et-1 |
x |
x 2 |
et-1x |
et-1 2 |
1 |
44,5669 |
34,8336 |
253,0000 |
64009,0000 |
8812,9053 |
1213,3809 |
2 |
-13,5349 |
44,5669 |
887,0000 |
786769,0000 |
39530,8530 |
1986,2099 |
3 |
1,3584 |
-13,5349 |
982,0000 |
964324,0000 |
-13291,2576 |
183,1931 |
4 |
-45,7460 |
1,3584 |
1534,0000 |
2353156,0000 |
2083,7516 |
1,8452 |
5 |
-278,7080 |
-45,7460 |
4264,0000 |
18181696,0000 |
-195061,0651 |
2092,6991 |
6 |
40,1136 |
-278,7080 |
188,0000 |
35344,0000 |
-52397,1111 |
77678,1702 |
7 |
277,1774 |
40,1136 |
4113,0000 |
16916769,0000 |
164987,3554 |
1609,1032 |
8 |
23,3934 |
277,1774 |
548,0000 |
300304,0000 |
151893,2190 |
76827,3149 |
9 |
20,6201 |
23,3934 |
393,0000 |
154449,0000 |
9193,5920 |
547,2495 |
10 |
25,7642 |
20,6201 |
321,0000 |
103041,0000 |
6619,0664 |
425,1904 |
11 |
-205,5553 |
25,7642 |
3313,0000 |
10975969,0000 |
85356,7868 |
663,7939 |
12 |
-71,4553 |
-205,5553 |
1472,0000 |
2166784,0000 |
-302577,4570 |
42252,9968 |
13 |
-446,0479 |
-71,4553 |
5850,0000 |
34222500,0000 |
-418013,5992 |
5105,8622 |
14 |
15,1721 |
-446,0479 |
492,0000 |
242064,0000 |
-219455,5527 |
198958,7036 |
15 |
46,1217 |
15,1721 |
59,0000 |
3481,0000 |
895,1522 |
230,1918 |
16 |
-1,2147 |
46,1217 |
602,0000 |
362404,0000 |
27765,2777 |
2127,2134 |
17 |
-14,2285 |
-1,2147 |
1317,0000 |
1734489,0000 |
-1599,7281 |
1,4754 |
18 |
44,2415 |
-14,2285 |
374,0000 |
139876,0000 |
-5321,4722 |
202,4512 |
19 |
42,8070 |
44,2415 |
133,0000 |
17689,0000 |
5884,1184 |
1957,3096 |
20 |
30,1776 |
42,8070 |
281,0000 |
78961,0000 |
12028,7677 |
1832,4395 |
21 |
38,7110 |
30,1776 |
181,0000 |
32761,0000 |
5462,1384 |
910,6852 |
22 |
227,4389 |
38,7110 |
11188,0000 |
125171344,0000 |
433098,3025 |
1498,5390 |
23 |
40,5750 |
227,4389 |
124,0000 |
15376,0000 |
28202,4195 |
51728,4381 |
24 |
2366,8597 |
40,5750 |
8312,0000 |
69089344,0000 |
337259,4771 |
1646,3314 |
25 |
15,2548 |
2366,8597 |
409,0000 |
167281,0000 |
968045,5969 |
5602024,6031 |
26 |
-607,6043 |
15,2548 |
8294,0000 |
68790436,0000 |
126523,3074 |
232,7089 |
27 |
-75,0509 |
-607,6043 |
2686,0000 |
7214596,0000 |
-1632025,2483 |
369183,0300 |
28 |
117,0972 |
-75,0509 |
821,0000 |
674041,0000 |
-61616,7694 |
5632,6340 |
29 |
37,6974 |
117,0972 |
521,0000 |
271441,0000 |
61007,6219 |
13711,7456 |
30 |
30,4469 |
37,6974 |
313,0000 |
97969,0000 |
11799,2811 |
1421,0927 |
31 |
41,4043 |
30,4469 |
126,0000 |
15876,0000 |
3836,3056 |
927,0119 |
32 |
-35,9456 |
41,4043 |
1009,0000 |
1018081,0000 |
41776,9802 |
1714,3195 |
33 |
-276,5755 |
-35,9456 |
5364,0000 |
28772496,0000 |
-192812,4238 |
1292,0892 |
34 |
110,6214 |
-276,5755 |
2350,0000 |
5522500,0000 |
-649952,4572 |
76494,0148 |
35 |
-684,7142 |
110,6214 |
9057,0000 |
82029249,0000 |
1001897,7578 |
12237,0877 |
36 |
-268,1480 |
-684,7142 |
4234,0000 |
17926756,0000 |
-2899080,0563 |
468833,5789 |
37 |
-621,1375 |
-268,1480 |
8019,0000 |
64304361,0000 |
-2150278,9358 |
71903,3582 |
38 |
41,7616 |
-621,1375 |
239,0000 |
57121,0000 |
-148451,8548 |
385811,7537 |
39 |
-68,5487 |
41,7616 |
1602,0000 |
2566404,0000 |
66902,0693 |
1744,0305 |
SUMA |
-34,8336 |
68,5487 |
92225,0000 |
563541511,0000 |
-5341072,8850 |
7484843,8461 |
Tabela 2.2. Ciąg dalszy obliczeń z tabeli 2.1
t |
etx |
et-1et |
ê |
r |
r2 |
et 2 |
1 |
11275,4293 |
1552,4269 |
-1,3893 |
45,9562 |
2111,9745 |
1986,2099 |
2 |
-12005,4435 |
-603,2081 |
0,0069 |
-13,5418 |
183,3813 |
183,1931 |
3 |
1333,9270 |
-18,3855 |
-3,5619 |
4,9203 |
24,2089 |
1,8452 |
4 |
-70174,4076 |
-62,1404 |
-1,9390 |
-43,8070 |
1919,0518 |
2092,6991 |
5 |
-1188411,0719 |
12749,7858 |
-1,5732 |
-277,1348 |
76803,6907 |
77678,1702 |
6 |
7541,3622 |
-11179,9908 |
-21,3578 |
61,4715 |
3778,7398 |
1609,1032 |
7 |
1140030,6748 |
11118,5916 |
3,6875 |
273,4899 |
74796,7151 |
76827,3149 |
8 |
12819,5634 |
6484,1119 |
14,3455 |
9,0479 |
81,8636 |
547,2495 |
9 |
8103,7168 |
482,3745 |
-1,9430 |
22,5631 |
509,0957 |
425,1904 |
10 |
8270,3074 |
531,2615 |
-2,2074 |
27,9716 |
782,4084 |
663,7939 |
11 |
-681004,8336 |
-5295,9683 |
1,7945 |
-207,3499 |
42993,9671 |
42252,9968 |
12 |
-105182,2253 |
14688,0216 |
-15,1402 |
-56,3151 |
3171,3899 |
5105,8622 |
13 |
-2609380,0476 |
31872,4916 |
-1,2557 |
-444,7922 |
197840,0863 |
198958,7036 |
14 |
7464,6593 |
-6767,4703 |
-31,5991 |
46,7712 |
2187,5443 |
230,1918 |
15 |
2721,1817 |
699,7621 |
-2,8748 |
48,9965 |
2400,6603 |
2127,2134 |
16 |
-731,2349 |
-56,0229 |
-0,2445 |
-0,9701 |
0,9412 |
1,4754 |
17 |
-18738,9811 |
17,2831 |
-2,3688 |
-11,8597 |
140,6524 |
202,4512 |
18 |
16546,3180 |
-629,4916 |
-4,3528 |
48,5943 |
2361,4041 |
1957,3096 |
19 |
5693,3314 |
1893,8457 |
-0,9400 |
43,7470 |
1913,7970 |
1832,4395 |
20 |
8479,8945 |
1291,8109 |
-0,8491 |
31,0267 |
962,6562 |
910,6852 |
21 |
7006,6851 |
1168,2026 |
-1,7731 |
40,4841 |
1638,9600 |
1498,5390 |
22 |
2544586,0422 |
8804,3785 |
12,2900 |
215,1489 |
46289,0312 |
51728,4381 |
23 |
5031,3012 |
9228,3341 |
10,6696 |
29,9054 |
894,3329 |
1646,3314 |
24 |
19673337,4114 |
96035,3523 |
8,8752 |
2357,9845 |
5560090,8718 |
5602024,6031 |
25 |
6239,2130 |
36105,9695 |
146,7281 |
-131,4733 |
17285,2264 |
232,7089 |
26 |
-5039470,3684 |
-9268,8824 |
7,2469 |
-614,8513 |
378042,0740 |
369183,0300 |
27 |
-201586,6535 |
45601,2378 |
-39,1517 |
-35,8991 |
1288,7478 |
5632,6340 |
28 |
96136,7708 |
-8788,2447 |
-7,6618 |
124,7589 |
15564,7891 |
13711,7456 |
29 |
19640,3369 |
4414,2567 |
4,1581 |
33,5393 |
1124,8844 |
1421,0927 |
30 |
9529,8704 |
1147,7674 |
-1,1339 |
31,5808 |
997,3479 |
927,0119 |
31 |
5216,9470 |
1260,6326 |
-1,8236 |
43,2279 |
1868,6537 |
1714,3195 |
32 |
-36269,1528 |
-1488,3056 |
-0,0438 |
-35,9019 |
1288,9433 |
1292,0892 |
33 |
-1483551,0556 |
9941,6844 |
0,3997 |
-276,9752 |
76715,2875 |
76494,0148 |
34 |
259960,2220 |
-30595,1625 |
-18,5666 |
129,1880 |
16689,5301 |
12237,0877 |
35 |
-6201456,7950 |
-75744,0271 |
14,2336 |
-698,9478 |
488528,0312 |
468833,5789 |
36 |
-1135338,6973 |
183604,7623 |
-42,1413 |
-226,0067 |
51079,0255 |
71903,3582 |
37 |
-4980901,3529 |
166556,7793 |
-11,0678 |
-610,0697 |
372185,0045 |
385811,7537 |
38 |
9981,0203 |
-25939,6891 |
-43,0163 |
84,7778 |
7187,2837 |
1744,0305 |
39 |
-109815,0897 |
-2862,7047 |
0,7074 |
-69,2561 |
4796,4081 |
4698,9305 |
SUMA |
-7071,2244 |
467951,4307 |
-34,8336 |
0,0000 |
7458518,6616 |
7488329,3956 |
Posługując się danymi z tabeli obliczam macierze potrzebne do oszacowania modelu pomocniczego:
Wyznaczam macierz XTX*
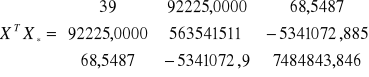
Wyznaczam macierz (XTX)* -1
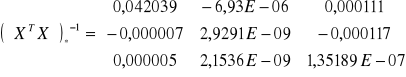
Wyznaczam macierz XTY*
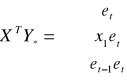
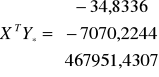
Wyznaczam parametry modelu pomocniczego
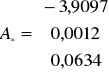
a1= -3,9097
b1= 0,0012
c1= 0,0634
Model pomocniczy oszacowany êt :
êt = -3,9097+0,0012x1+0,0634et-1
Obliczamy współczynnik determinacji R2 :
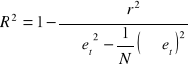
![]()
![]()
![]()
![]()
![]()
![]()
Wniosek: Model w 0,398 % wyjaśnia zmienność zmiennej objaśnianej (czyli reszt nie opóźnionych) a w 99,602% nie wyjaśnia .
Stawiamy hipotezy:
H0: ρ0= 0 brak autokorelacji I rzędu
H1: ρ0≠ 0 istnieje autokorelacja I rzędu
, gdzie liczba obserwacji wynosi: n=40
Jeżeli: (n-1)R2 > χ2 -wówczas odrzucamy hipotezę H0 na rzecz hipotezy H1
Wartość krytyczną testu χ*2 odczytujemy z tablic rozkładu chi kwadrat(χ2) przy α=0,05 i 1 stopniu swobody
![]()
![]()
0,1511< 3,841
Wniosek: Nie ma podstaw do odrzucenia hipotezy H0 , brak autokorelacji I rzędu, model jest poprawny.
Praca pochodzi z serwisu www.e-sciagi.pl
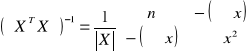
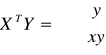
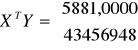
![]()
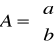
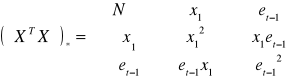
![]()
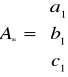
![]()
![]()
Wyszukiwarka
Podobne podstrony:
model ekonometryczny dwutlenek siarki ZXH5VNBVEUCZYXYD4R7OW6X5IV4PLLMNPT6OMUA
Model Ekonometryczny2, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
model ekonometryczny, Studia ZiIP GiG AGH, Magisterskie, Ekonometria
Model ekonometryczny 3, Ekonometria
Model ekonometryczny PKB na 1 mieszkańca, Planowianie obszarów wiejskich, Ekonometria
model ekonometryczny ?zrobocie (20 stron) MRWQ2WPWHO5WOMBISJJHWICZS2A7AB2SJ35L2NI
model ekonometryczny wywołń stron WWW (13 str)
Model ekonometryczny eksport (16 stron)
Model ekonometryczny aktywność zawodowa
ekonometria, Model ekonometryczny, Model ekonometryczny
mazurkiewicz,Ekonometria L, model ekonometryczny - ceny jabłek w poszczególnych województwach , Ekon
Model ekonometryczny 11- zużycie energii (14 stron)
model ekonometryczny wynagrodzenia (9 stron) PDUCR5WASLTPGFE2QNTJHDAPEFS3BF6X5DV2NXY
Model ekonometryczny 8 ?zrobocie (15 stron)k
więcej podobnych podstron