1. Wstęp

Celem ćwiczenia jest zapoznanie się z wybranymi własnościami materiałów ferroelektrycznych, wyznaczenie zależności przenikalności elektrycznej kryształu ferroelektrycznego od temperatury w fazie ferroelektrycznej i paraelektrycznej
i określenie temperatury przejścia fazowego (temperatury Curie-Weissa).

Względna przenikalność elektryczna większości dielektryków krystalicznych nie ulega niemalże zmianie wraz ze zmianą temperatury. Oznacza to, że właściwości dielektryczne ciał stałych wiążą się z rozkładem ładunku wewnątrz cząsteczek, nie zależą natomiast od ruchu cieplnego tych ostatnich. Inaczej mówiąc, w dielektrykach stałych zachodzi indukowana polaryzacja elektronowa. Polaryzacji zorientowanej nie obserwuje się nawet w tych kryształach, które zbudowane są z cząsteczek dipolowych. W kryształach ujawnia się bardzo silne oddziaływanie wzajemne cząsteczek, w związku z czym zwykle (pod względem wartości) natężenia nie są w stanie obracać cząsteczek
i ustawiać ich wzdłuż linii sił pola.

Istnieje grupa dielektryków, które mogą wykazywać spolaryzowanie spontaniczne (samoistne), występujące pod nieobecność zewnętrznego pola elektrycznego. Zjawisko to odkryte zostało początkowo w soli Seignette'a. Stąd inne substancje wykazujące podobne właściwości nazwano segnetoelektrykami (ferroelektrykami - oba terminy
są zamienne). Cechy charakterystyczne ferroelektryków to: przenikalność elektryczna sięgająca kilku tysięcy (dla zwykłych dielektryków przenikalność jest rzędu kilku,
w wyjątkowych przypadkach, np. wody, kilkudziesięciu), nieliniowa zależność wektorów polaryzacji P i natężenia pola elektrycznego E (stąd przenikalność jest
tu wielkością zależną od natężenia pola elektrycznego), wartość spolaryzowania
P zależy nie tylko od wartości pola E, lecz również od jego wartości wcześniejszych (zależność P od E przyjmuje postać pętli histerezy).

rys.1. Pętla histerezy wektorów E i P. Jak widać, wartość wektora polaryzacji P zależy od historii (wcześniejszych wartości) wektora E.

Duże wartości względnej przenikalności elektrycznej ferroelektryka uwarunkowane
są osobliwościami procesu jego polaryzacji. Monokryształ ferroelektryka rozdzielony jest na szereg spontanicznie spolaryzowanych obszarów - domen. Ta spontaniczna polaryzacja stanowi wynik zorientowania momentów dipolowych wszystkich cząsteczek wewnątrz domeny w pewnym określonym kierunku. W przypadku braku pola zewnętrznego obszary spontanicznej polaryzacji rozkładają się w ten sposób,
że elektryczne momenty dipolowe różnych domen równoważą się wzajemnie.
Po wprowadzeniu kryształu ferroelektryka w obręb zewnętrznego pola elektrycznego następuje zmiana orientacji momentów elektrycznych domen i kryształ staje się spolaryzowany.

Doświadczenie wykazuje, że spontaniczna orientacja momentów dipolowych, pociągająca za sobą tworzenie się domen, zachodzi w określonym zakresie temperatur - między tzw. punktami Curie (górnym i dolnym). Powyżej górnego punktu Curie występuje faza nieuporządkowana, przy czym w przypadku braku zewnętrznego pola elektrycznego dielektryk nie jest spolaryzowany. Poniżej występuje faza uporządkowana, charakteryzująca się występowaniem polaryzacji spontanicznej
w domenach. Poniżej dolnego punktu Curie zachodzą zjawiska prowadzące do rozpadu obszarów spontanicznej polaryzacji.

2. Układ pomiarowy i przebieg wykonania ćwiczenia

W pobliżu przejścia fazowego ferroelektryk-paraelektryk przenikalność zmienia
się z temperaturą zgodnie z prawem Curie-Weissa opisanym wzorem (1)

(1)

gdzie K - stała Curie-Weissa, ε - względna przenikalność, T - temperatura,
T_C - temperatura przejścia fazowego (stała). Po przekształceniu otrzymujemy wzór
na odwrotność przenikalności (2).

(2)

Jak widać, jest to zależność liniowa, której współczynniki można obliczyć metodą najmniejszych kwadratów.

Przenikalność elektryczną wyznaczamy poprzez pomiar pojemności C kondensatora płaskiego, którego okładki przylegają do płytki wyciętej z kryształu badanej substancji. Wzór na pojemność kondensatora płaskiego (3), który jest wzorem przybliżonym,
w naszym doświadczeniu, ze względu na małą grubość płytki d w stosunku do jej wymiarów (do powierzchni elektrod przylegających do badanej próbki - jego okładek), możemy uważać za słuszny

(3)

gdzie S - jest powierzchnią okładek, a ε₀ - jest przenikalnością elektryczną próżni.
Po przekształceniu otrzymujemy wzór na ε (4).

(4)

W naszym doświadczeniu pomiarów dokonujemy dwa razy, najpierw „ręcznie”,
a później wykorzystując komputerowy zestaw pomiarowy. Kryształ ferroelektryka zamknięty jest w komorze ogrzewanej wodą. Zmianę i stabilizację temperatury zapewnia ultratermostat. Pojemność próbki mierzona jest miernikiem automatycznym. Ze wzrostem temperatury przenikalność ferroelektryka rośnie, co manifestuje się zwiększeniem pojemności. Powyżej temperatury przejścia fazowego Tc, to znaczy
w fazie paraelektrycznej, obserwuje się spadek pojemności. Skrócona procedura pomiarowa, pierwszego pomiaru: podłączamy mierniki do próbki i włączamy
je, wybieramy odpowiedni zakres pomiarowy, uruchamiamy termostat, nastawiamy temperaturę o około 5 K wyższą od temperatury otoczenia, po ustaleniu się temperatury odczytujemy jej wartość i wartość pojemności, powtarzamy pomiary podwyższając temperaturę o około 1 K aż do temperatury około 340 K. Następnie wyłączamy grzanie w ultratermostacie i wraz ze spadkiem temperatury notujemy wskazania mierników (analogicznie jak przy grzaniu, co 1 K). Po zakończeniu pomiarów wyłączamy termostat i mierniki.

W drugiej części doświadczenia dane zbieramy przy pomocy mierników podłączonych do komputera za pomocą odpowiedniego programu (w węższym zakresie temperatur, tzn. w pobliżu punktu Curie). W rezultacie działania programu otrzymujemy zależność temperatury i pojemności w funkcji czasu. Dane trzeba później oczywiście odpowiednio „obrobić”, tak aby uzyskać zależność pojemności od temperatury, ale ten proces będzie dokładniej opisany w punkcie 4.

3. Tabele z wartościami wielkości zmierzonych w trakcie eksperymentu

Tabela 1. Dane zebrane podczas pierwszej części pomiarów: faza ocieplania

T [°C]	C [nF]	T [°C]	C [nF]	T [°C]	C [nF]
26,0	0,354	43,0	0,642	53,0	0,391
27,0	0,367	43,5	0,662	53,5	0,367
28,0	0,371	44,0	0,680	54,0	0,336
29,0	0,385	44,5	0,702	54,5	0,317
30,0	0,390	45,0	0,723	55,0	0,298
31,0	0,405	45,5	0,756	56,0	0,274
32,0	0,411	46,0	0,789	57,0	0,243
33,0	0,426	46,5	0,825	58,0	0,233
34,0	0,443	47,0	0,874	59,0	0,215
35,0	0,454	47,5	0,914	60,0	0,199
36,0	0,470	48,0	0,981	61,0	0,193
37,0	0,478	48,5	1,073	62,0	0,178
38,0	0,498	49,0	1,167	63,0	0,174
39,0	0,529	49,5	1,002	64,0	0,161
40,0	0,549	50,0	0,811	65,0	0,157
40,5	0,555	50,5	0,676	66,0	0,154
41,0	0,571	51,0	0,680	67,0	0,142
41,5	0,588	51,5	0,516	68,0	0,139
42,0	0,606	52,0	0,472	-	-
42,5	0,624	52,5	0,425	-	-

Tabela 2. Dane zebrane podczas pierwszej części pomiarów: faza ostygania

T [°C]	C [nF]	T [°C]	C [nF]	T [°C]	C [nF]
68,0	0,136	52,5	0,400	41,5	1,112
67,0	0,136	52,0	0,460	41,0	1,070
66,0	0,137	51,5	0,502	40,5	1,033
65,0	0,149	51,0	0,572	40,0	0,996
64,0	0,152	50,5	0,670	39,0	0,938
63,0	0,155	50,0	0,811	38,0	0,885
62,0	0,168	49,5	1,055	37,0	0,845
61,0	0,173	49,0	1,591	36,0	0,814
60,0	0,188	48,5	2,780	35,0	0,777
59,0	0,194	48,0	2,366	34,0	0,750
58,0	0,211	47,5	2,010	33,0	0,716
57,0	0,229	47,0	1,826	32,0	0,688
56,0	0,250	46,5	1,785	31,0	0,669
55,0	0,283	44,0	1,470	30,0	0,644
54,5	0,301	43,5	1,388	29,0	0,622
54,0	0,321	43,0	1,303	28,0	0,605
53,5	0,342	42,5	1,224	27,0	0,582
53,0	0,374	42,0	1,164	-	-

Tabela 3. Dane zebrane zestawem komputerowym*

T [°C]	C [nF]	ε	1/ε	T [°C]	C [nF]	ε	1/ε
49,09	1,733	2352,1	0,00043	48,78	2,126	2900,7	0,00034
49,07	1,366	1839,8	0,00054	48,76	2,192	2992,8	0,00033
49,05	1,724	2339,5	0,00043	48,74	2,263	3091,9	0,00032
49,03	1,718	2331,2	0,00043	48,72	2,419	3309,7	0,00030
49,01	1,652	2239,0	0,00045	48,70	2,607	3572,1	0,00028
48,99	1,728	2345,1	0,00043	48,68	2,383	3259,4	0,00031
48,97	1,751	2377,2	0,00042	48,66	2,809	3854,1	0,00026
48,95	1,864	2535,0	0,00039	48,64	2,442	3341,8	0,00030
48,94	1,810	2459,6	0,00041	48,62	2,522	3453,5	0,00029
48,92	1,496	2021,3	0,00049	48,60	3,184	4377,5	0,00023
48,90	1,961	2670,4	0,00037	48,58	3,353	4613,4	0,00022
48,88	1,606	2174,8	0,00046	48,57	2,753	3775,9	0,00026
48,86	1,774	2409,3	0,00042	48,55	3,496	4813,1	0,00021
48,84	1,999	2723,4	0,00037	48,53	2,893	3971,3	0,00025
48,82	2,041	2782,0	0,00036	48,51	3,049	4189,1	0,00024
48,80	2,093	2854,6	0,00035	48,49	3,661	5043,4	0,00020

* dla przejrzystości zebrano dane tylko dla temperatur odpowiadających fazie paraelektrycznej blisko temperatury przejścia fazowego; punkty te będą układać się na linii prostej

Tabela 4. Dane badanej próbki kryształu TGS i tablicowe wartości użyte podczas wykonywania dalszych obliczeń.

powierzchnia elektrod	(89±6) [mm^2]
grubość płytki	(1,1±0,1) [mm]
pojemność dodatkowa	48 [pF]
przenikalność elektryczna próżni ε0	8,854187·10^-12 [F/m]

4. Opracowanie wyników

Przejście fazowe następuje w temperaturze w pobliżu punktu dla którego wartość przenikalności jest największa. Na tej podstawie nasze dane możemy podzielić na część związaną z fazą ferroelektryczną i na część związaną z fazą paraelektryczną. Stosując metodę najmniejszych kwadratów, możemy dopasować do naszych danych krzywe wielomianowe wyższego stopnia (np. 4-go, dla których współczynnik determinacji będzie wystarczająco duży).

Poniżej znajdują się wykresy zależności uzyskanych podczas doświadczenia.
Do obliczeń współczynników wielomianów i współczynnika determinacji wykorzystano arkusz kalkulacyjny MS Excel.

wykres 1. Zależność przenikalności ε od temperatury T (pierwsza seria pomiarowa, faza ocieplania).

wykres 2. Zależność odwrotności przenikalności 1/ε od temperatury T (pierwsza seria pomiarowa, faza ocieplania).

wykres 3. Zależność przenikalności ε od temperatury T (pierwsza seria pomiarowa, faza oziębiania).

wykres 4. Zależność odwrotności przenikalności 1/ε od temperatury T (pierwsza seria pomiarowa, faza oziębiania).

wykres 5. Zależność przenikalności ε od temperatury T (druga seria pomiarowa - dane komputerowe). Górna funkcja opisuje fazę ferroelektryczną, a dolna paraelektryczną.

wykres 6. Zależność odwrotności przenikalności 1/ε od temperatury T (druga seria pomiarowa - dane komputerowe). Górna funkcja opisuje fazę ferroelektryczną, a dolna paraelektryczną.

wykres 7. Zależność odwrotności przenikalności 1/ε od temperatury T (druga seria pomiarowa - dane komputerowe, punkty bliskie temperaturze przejścia fazowego z Tabeli 3).

Zastosowanie metody najmniejszych kwadratów do obliczeń współczynników krzywych 3-go i 4-go stopnia wymaga użycia dużo bardziej skomplikowanych wzorów, niż w przypadku obliczeń współczynników zależności liniowej. Opis postępowania przy ich obliczaniu zawiera odnośnik literaturowy [3]. Dla nas dokładności współczynników krzywych 3-go i 4-go stopnia są mało istotne. Na podstawie wyników doświadczenia możemy jedynie wyznaczyć orientacyjne krzywe, które pozwolą nam ocenić kształt rzeczywistych wykresów funkcji ε (T) i 1/ε (T).

Dla danych uzyskanych „ręczną” metodą zbierania wyników, do obliczeń współczynników zależności (2) możemy wykorzystać wszystkie wyniki dla faz paraelektrycznych (dla nich właśnie działa prawo Curie-Weissa). Analizując wykresy
2 i 4 widzimy, że punkty doświadczalne dość dobrze pasują do linii prostej. Dla wykresu 6, widzimy, że będziemy musieli raczej wykorzystać punkty bliskie temperaturze przejścia, gdyż tylko one układają się w miarę dobrze na linii prostej.

Należy jeszcze opisać metodę tworzenia wykresów dla danych komputerowych.
Po przeprowadzeniu tej fazy doświadczenia program komputerowy wygenerował nam dwa plik - jeden z zależnością temperatury od czasu (z dokładnością do części całkowitej temperatury w stopniach Celsjusza), a drugi z zależnością pojemności próbki od czasu. Do zależności temperatury od czasu dopasowaliśmy krzywą wielomianową
3-go stopnia (współczynnik determinacji wyniósł 0,9939) i na tej podstawie wyznaczyliśmy temperatury pośrednie (potrzebowaliśmy po prostu mieć większą dokładność pomiaru temperatury, niż tylko do części całkowitej).

Zależność (2) jest funkcją liniową postaci y=Bx+A. Dla nas wartości y to
1/ε, argumenty x to T, współczynnik B jest odwrotnością stałej Curie K, a współczynnik A jest co do modułu równy ilorazowi temperatury Curie T_C i stałej Curie K. Do obliczeń współczynników prostej możemy zaprząc metodę najmniejszych kwadratów. Współczynniki obliczymy korzystając ze wzorów (5), (6), (7)

(5)

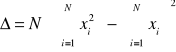
(6)

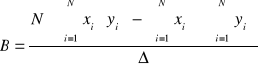
(7)

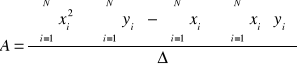
gdzie N jest ilością pomiarów. Następnie obliczymy stałe Curie K i temperatury Curie T_C korzystając ze wzorów (8) i (9).

(8)

(9)

Obliczenia wykonujemy dla pierwszej serii pomiarowej, dla obu faz - ocieplania
i oziębiania, oraz dla punktów z drugiej serii pomiarowej (dane komputerowe) zestawionych w Tabeli 3.

5. Rachunek błędów

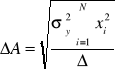
Do obliczenia niepewności współczynników prostej wykorzystamy również metodę najmniejszych kwadratów. Poszukiwane wartości znajdziemy korzystając ze wzorów (10), (11) i (12).

(10)

(11)

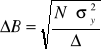
(12)

Następnie obliczymy niepewności wyznaczenia stałej K i temperatury
T_C (na podstawie metody różniczki zupełnej), w oparciu o wzory (13) i (14).

(13)

(14)

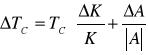
Warto nadmienić, że wykresy 2, 4 i 7 posiadają zaznaczone niepewności pomiarowe obliczone zgodnie z metodą najmniejszych kwadratów. Jak już było wspomniane, dla krzywych wyższego stopnia niepewności wyznaczenia współczynników nie mają tak wielkiego znaczenia i nie zostały uwzględnione (wykresy te możemy traktować jedynie jako pewien pogląd na rzeczywisty wygląd wykresów szukanych zależności). Wzór
z którego policzono współczynnik determinacji to wzór (15).

(15)

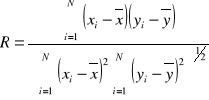
6. Zapis końcowy

Wyniki obliczeń naszych stałych Curie i temperatur Curie zbiera Tabela 5.

Tabela 5. Zestawienie wyników obliczeń stałej Curie K i temperatur przejścia T_C

	K [K]	TC [°C]
1 seria - faza ocieplania	2630±30	48±1
1 seria - faza oziębiania	2360±25	48±1
2 seria - dane komputerowe	2200±160	48±7

7. Wnioski

Badanym kryształem ferroelektrycznym był siarczan trójglicyny, który w skrócie oznacza się TGS. Paradoksalnie dokładniejsze wyniki uzyskaliśmy dla pomiarów „ręcznych”, niż tych uzyskanych komputerowo. Co do temperatury Curie, możemy nasz wynik 48 °C traktować jako wartość występującą w rzeczywistości. Wszystkie trzy obliczenia dały nam ten sam wynik (jako najbardziej prawdopodobny) tyle, że z różną dokładnością. Dla pomiarów ręcznych względna niepewność wyznaczenia temperatury Curie jest na poziomie 1% (!). Jest to wręcz rewelacyjna dokładność jak na warunki pracowni fizycznej. W przypadku pomiarów komputerowych względna niepewność wyznaczenia temperatury Curie jest na poziomie 7%. W dalszej części wniosków przeanalizujemy możliwe przyczyny mniejszej dokładności pomiarów komputerowych.

Względna niepewność wyznaczenia stałej Curie dla „ręcznej” metody zbierania danych jest na poziomie 1%, podobnie jak dla temperatury. Dane dla fazy ocieplania
są jedynie orientacyjne. Spontaniczny proces przejścia fazowego zachodzi dopiero przy swobodnym oziębianiu się naszej próbki. Dlatego bardziej należałoby się skłaniać dla tej właśnie wartości jako najbardziej prawdopodobnej. Względna niepewność wyznaczenia stałej Curie dla pomiarów komputerowych jest na poziomie 7%. Znów względna niepewność sugeruje nam większe zaufanie do wyników uzyskanych „ręczną” metodą zbierania danych niż dla tej komputerowej.

Zauważmy jeszcze, że dla fazy oziębiania (dla pomiarów „ręcznych” - Tabela 2) dla temperatur od 44,5 °C do 46 °C nie zanotowaliśmy wartości pojemności. Wskazania mierników w tym zakresie temperatur zmieniały się tak szybko, że odczyt był niemożliwy ze względu na bezwładność mierników (nie zdążały się one ustabilizować
i wyświetlić wyniku). Było to spowodowane zwiększeniem się pojemności cieplnej próbki ferroelektryka w tym zakresie temperatur. W pobliżu temperatury przejścia fazowego taki właśnie, gwałtowny wzrost pojemności cieplnej jeszcze w fazie ferroelektrycznej powinien mieć miejsce. Nasuwa to jeszcze wniosek, że istotnie wyniki pomiarów dla fazy ocieplania miały charakter jedynie przybliżony i orientacyjny. Również porównując wartości pojemności dla fazy ocieplania (Tabela 1) i dla fazy oziębiania (Tabela 2), dochodzimy do wniosku, że o wiele większa zmienność wyników ma miejsce w przypadku fazy oziębiania.

Jak już napisaliśmy, wyniki uzyskane drogą pomiaru komputerowego wydają się
o wiele mniej dokładne i prawdopodobne niż te zebrane ręcznie. Wynika to głównie
z metod wykorzystywanych przez komputer do pomiaru pojemności. Pomiaru dokonaliśmy podwyższając temperaturę próbki do około 56 °C i pozwalając jej swobodnie ostygać. Pomiary dokonywane były co 1, 2 sekundy. Naszym zdaniem mierniki miały za mało czasu na ustabilizowanie się i podanie prawidłowego wyniku
do komputera. Jak widać z wykresów 5 i 6 rozrzut punktów pomiarowych jest bardzo duży. Dopasowanie krzywych jest o wiele gorsze niż w przypadku „ręcznej” metody zbierania danych. Współczynniki determinacji są o wiele mniejsze. Możemy zatem wysnuć wniosek, że komputer jest tylko maszyną i nie zastąpi uważnego eksperymentatora.

8. Literatura

1. Kurs fizyki, B. Jaworski, A. Dietłaf, L. Miłkowska, tom 2, PWN, Warszawa 1984, str. 112-116.

2. Tablice matematyczne fizyczne chemiczne astronomiczne, T. Szymczyk,
   S. Rabiej, A. Pielesz, J. Desselberger, PPU „Park”, Bielsko-Biała 2001,
   str. 172.

1. Wstęp do Analizy Błędu Pomiarowego, John R. Taylor, PWN, Warszawa 1995, str. 172-187.

2. Wykłady z fizyki, I. W. Sawieliew, tom 2, PWN, Warszawa 1998, str. 100-102.

2

---