Politechnika Śląska Gliwice 98.03.25

Wydział Elektryczny

Studia wieczorowe

Semestr II gr.2

SPRAWOZDANIE Z LABORATORIUM FIZYCZNEGO

TEMAT: Polaryzacja.

Sprawdzanie prawa Malusa oraz stałej Verdeta.

Marszałek Krzysztof

Witkowski Adam

4.

PRZEBIEG ĆWICZENIA: Prawo Malusa

1. Łączymy obwód według schematu.

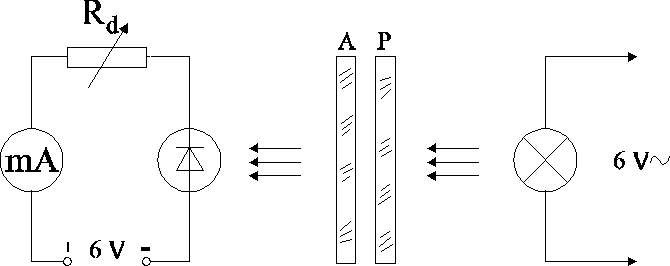
2. Ustalamy taką wartość oporu R_d , aby przy kącie  = wychylenie miernika nie przekraczało zakresu pomiarowego.

3. Zmieniając kąt skręcenia filtrów polaryzacyjnych w przedziale co , notujemy wskazania miliamperomierza.

4. Dla każdego kąta wykonujemy po trzy pomiary.

5. Rysujemy wykres (we współrzędnych biegunowych) zależności wskazań miernika od kąta skręcenia filtrów polaryzacyjnych.

6. Rysujemy wykres zależności wskazań miernika od cos² .

7. Przeprowadzamy graficzną analizę błędów.

5.

PRZEBIEG ĆWICZENIA: Stała Vereta

1. Łączymy obwód cewki.

2. Zmieniając natężenie prądu płynącego przez cewkę w zakresie od 14 A do 0 co 1A, mierzymy trzykrotnie kąt skręcenia płaszczyzny polaryzacji.

3. Rysujemy wykres zależności kąta skręcenia płaszczyzny polaryzacji od natężenia prądu:

 = k·I , gdzie:

k = _bnl - współczynnik proporc. obliczony metodą regresji liniowej.

4. Obliczamy stałą Verdeta:

5. Przeprowadzamy rachunek błędów.

6.

Tabele pomiarowe:

1.Tabela (Prawo Malusa)

Kąt   	Wskazanie miernika [mA]
	Skręcenie w lewo			Skręcenie w prawo
	1	2	3	1	2	3
0	75	75	75	75	75	75
15	70	71	71	73	73	73
30	62	62	61	65	63	64
45	45	45	45	50	50	50
60	25	24	23	28	28	28
75	5	5	5	8	8	8
90	0,5	0,5	0,5	0,5	0,5	0,5

2.Tabela (Stała Verdeta)

I [A]	Kąt skręcenia  [ ]
	1	2	3
14	-	-	-
13	10,8	10,8	10,8
12	10,2	10,1	10,1
11	9,1	9,1	9,2
10	8,4	8,4	8,3
9	7,4	7,4	7,3
8	6,5	6,6	6,5
7	5,7	5,7	5,7
6	4,8	4,8	4,8
5	3,85	3,8	3,85
4	2,95	2,95	2,95
3	2,1	2,1	2,1
2	1,4	1,4	1,35
1	0,45	0,45	0,45
0	-0,5	-0,5	-0,5

7.

Opracowanie wyników pomiarów, oraz ich błędów.

l = 20 cm = 0.2 m - długość kuwety

n = 60 - liczba zwojów na jednostkę długości cewki

b = 116 - stała aparaturowa

k = (91.6 ± 0.9)·10^-2 - współczynnik proporcjonalności obliczony metodą regresji liniowej przez komputer

_ = 4·10^-7 - przenikalność magnetyczna próżni

Korzystając z powyższych danych obliczamy stałą Verdeta:

Metodą pochodnej logarytmicznej obliczamy błąd bezwzględny:

Po odpowiednim zaokrągleniu wyznaczona stała Verdeta wynosi:

Ostatecznie można powiedzieć, że ćwiczenie zostało wykonane poprawnie gdyż wyznaczona doświadczalnie wartość stałej Verdeta dla jodku potasu jest zbliżona do wartości tablicowej, która wynosi

Błąd odczytu z mikroamperomierza:

Ze wzoru: D= Klasa %* Zakres /100%

Dla ćwiczenia nr1.

D= 0,5%*1,5/100%= 0,0075

Dla ćwiczenia nr2.

Podział na trzy zakresy.

D=0,2%*20/100%= 0,04

D=0,2%*10/100%= 0,02

D=0,2%*0/100%= 0

1.

Wprowadzenie:

Polaryzacja światła. Polaryzacja jest zjawiskiem polegającym na uporządkowaniu kierunków drgań fali poprzecznej. Występuje ono przy braku symetrii osiowej w źródle podczas przechodzenia przez ośrodek anizotropowy przy załamaniu i odbiciu na granicy dwóch ośrodków.

Polaryzacja przez odbicie. Zauważono, że światło odbite od szkła lub od innego dielektryka jest spolaryzowane. Stopień polaryzacji światła odbitego i załamanego określają wzory Fresnela. Np. gdy składowa wektora natężenia pola elektrycznego E jest prostopadła do płaszczyzny padania to:

- w świetle odbitym zachodzi warunek:

- dla światła załamanego:

Jeśli wiązka światła spolaryzowanego w płaszczyźnie prostopadłej do płaszczyzny padania ulegnie odbiciu pod kątem , zwanym kątem Brewstera, to natężenie wiązki odbitej z płaszczyzną równoległą jest równe zero. Czyli w odbitym świetle pozostaje jedynie spolaryzowana wiązka światła w płaszczyźnie padania, bo E_0ll = 0 i tg () = . Wynika z tego zależność: tg _B = n , gdzie n - współczynnik załamania materiału.

Jeżeli płaszczyzna polaryzacji światła padającego tworzy kąt  z płaszczy-zną padania, to płaszczyzna polaryzacji ulegnie skręceniu o kąt  :

Polaryzacja światła załamanego. Po przepuszczeniu przez płytkę płasko równoległą wiązki światła, jej część zostaje spolaryzowana (wzory Fresnela). Największa polaryzacja nastąpi jeśli światło pada na płytkę pod kątem Brewstera. Stopień polaryzacji można zwiększyć stosując wiele połączonych płytek, z tym że muszą być one bardzo cienkie, ażeby nie osłabić wiązki światła.

Dwójłomność kryształu. Dla kryształów anizotropowych występuje tzw. anomalne załamanie. Np. dla kryształu szpatu islandzkiego zjawisko to polega na rozdzieleniu wiązki światła. Jeśli oś optyczna kryształu nie jest równoległa do powierzchni kryształu to wiązka spolaryzowana w płaszczyźnie prostopadłej do płaszczyzny padania przechodzi przez kryształ bez załamania i nazywa się ją promieniem zwyczajnym. Załamanie światła nastąpi dla drugiej płaszczyzny polaryzacji, a promień nazywa się nadzwyczajnym. Zjawisko dwójłomności wskazuje na różne prędkości światła dla różnych płaszczyzn polaryzacji, a co za tym idzie dla różnych współczynników załamania. Istnieją także kryształy dwuosiowe np. cukier (krystaliczny), mika, gips. W kryształach tych otrzymujemy dwa promienie nadzwyczajne. Praktycznym zastosowaniem dwójłomności jest tzw. nikol lub inaczej kryształ Nikola. Jest to kryształ szpatu islandzkiego odpowiednio zeszlifowany, przecięty w płaszcz. prostopadłej do osi optycznej. Obie części kryształu są sklejone balsamem kanadyjskim. Po przejściu wiązki światła - promień zwyczajny ulega wewnętrznemu odbiciu na granicy szpat-balsam, a promień nadzwyczajny wychodzi z nikola pod kątem padania całkowicie spolaryzowany.

Dwójłomność wymuszona. Zjawisko to można wykorzystać do wizualizacji naprężeń w częściach np. maszyn. Jest tak, gdyż różnica współczynników załamania promieni zwyczajnego oraz nadzwyczajnego zależy od naprężenia p w materiale: n_n - n_z=kp , gdzie:  - długość fali, k - stała materiałowa.

J.Kerr odkrył dwójłomność wymuszoną w ciekłych dielektrykach umie- szczonych w poprzecznym polu elektr. Różnica współczynników załamania obu promieni jest proporcjonalna do kwadratu natężenia pola elektrycznego. Zwykle jako dielektryk stosuje się nitrobenzen, dla którego światło jest spolaryzowane pod kątem do kierunku pola elektrycznego. Ponieważ zjawisko to nie posiada żadnej bezwładności, to można je wykorzystać jako migawkę w kamerze przy zasilaniu napięciem o odpowiednio wysokiej częstotliwości.

A.Cotton i H.Mouton odkryli natomiast zjawisko dwójłomności wymuszonej dla cieczy organicznych umieszczonych w poprzecznym polu magnetycznym. Różnica współczynników załamania jest proporcjonalna do kwadratu indukcji magnetycznej w badanym materiale.

2.

SPRAWDZANIE PRAWA MALUSA

Jeśli naświetli się prostopadle płytkę kalcytową (odp. przyciętą w stosunku do osi optycznej) to po przejściu przez nią wiązka światła rozczepia się na promień zwyczajny i nadzwyczajny. Promień nadzwyczajny eliminujemy przesłoną, a pomiędzy ekranem i przesłoną umieszczamy nikol. Przy jego obrocie można zauważyć zmianę natężenia światła. Największa jego wartość nastąpi, gdy płaszczyzna polaryzacji nikola będzie równoległa do płaszczyzny kalcytu. Zjawisko to zawarł w swoim prawie Malus:

, gdzie:

I₀ - natężenie światła padającego

 - kąt pomiędzy płaszczyznami polaryzacji

Ażeby zbadać zależności energetyczne w świetle spolaryzowanym korzysta się z fotometru polaryzacyjnego. Składa się on ze źródła światła (żarówka) umieszczonego w tulei regulacyjnej zamkniętej filtrem polaryzacyjnym. Na drodze światła stoi następnie soczewka skupiająca, która daje równoległą wiązkę światła padającą na drugi filtr polaryzacyjny zwany analizatorem. Detektorem światła jest (w naszym przypadku) fotodioda FG2. Kąt skręcenia powierzchni polaryzacji, polaryzatora i analizatora odczytuje się ze skali. Ażeby umożliwić dobór natężenia prądu odpowiedniego dla zakresów stosowanego miliamperomierza, w obwodzie fotodiody umieszcza się opornicę dekadową. Natomiast aby wyeliminować fluktuancję światła spowodowaną zmianami napięcia zasilającego - stosuje się magnetyczny stabilizator napięcia.

3.

WYZNACZANIE STAŁEJ VERDETA

M. Faraday wykrył zjawisko skręcenia płaszczyzny polaryzacji w ośrodkach izotropowych umieszczonych w podłużnym polu magnetycznym. Kierunek skręcenia jest zgodny z kierunkiem prądu w solenoidzie, który wytwarza pole magnetyczne. Kierunek ten jest proporcjonalny do indukcji magnetycznej:

  Bl , gdzie:

l - droga przebyta przez światło w polu magnetycznym

 - stała Verdeta (zależy od rodzaju materiału).

Duże wartości stałej Verdeta osiąga się dla m.in. czterochlorku węgla, dwu-siarczku węgla. W naszym przypadku stosujemy roztwór jodku potasu o stężeniu bliskim nasyceniu. Teoria zjawiska Faradaya oparta jest na podstawie postulatów Fresnela.

Kuweta z badaną cieczą umieszczona jest wewnątrz solenoidu nałożonego na rurę polarymetru krzyżowego. Przez solenoid przepuszczamy prąd o dużym natężeniu. Indukcja magnetyczna wewnątrz solenoidu jest określona wzorem:

B =_ bnI [T] , gdzie:

n = 60 - liczba zwojów na jednostkę długości cewki

_ - przenikalność magnetyczna próżni

Współczynnik b = 116 jest stałą aparaturową, obliczoną metodą całkowania graficznego przy uwzględnieniu rozmiarów cewki, liczby warstw uzwojenia i grubości drutu nawojowego.

---