Model ekonometryczny

WIG

Na podstawie danych zawartych w prasie ekonomicznej badamy jaki wpływ na kształtowanie się Warszawskiego Indeksu Giełdowego (zmienna objaśniana) w przeciągu 10 dni funkcjonowanie giełdy mają następujące czynniki (zmienne kandydatki):

1. kształtowanie się ceny ropy w poszczególnych dniach (USD/baryłka) - x₁

2. kurs dolara względem złotego (zł) - x₂

3. kurs euro względem złotego (zł) - x₃

4. kurs średni w notowaniach ciągłych akcji PKN Orlen (zł) - x₄

5. poszczególne dni tygodnia notowań giełdowych - z₅:

• poniedziałek - 1

• wtorek - 2

• środa - 3

• czwartek - 4

• piątek - 5

Cel analityczno - opisowy.

Tabela przedstawia potrzebne informacje do przeprowadzenia badania:

Okres	WIG	Ropa	Dolar	Euro	PKN Orlen	Dzień
t	Y	X1	X2	X3	X4	X5
1	14503,33	24,75	3,9948	4,2981	17,21	1
2	14495,96	24,5	4,091	4,3231	17,56	2
3	14451,56	24,4	4,0554	4,3428	17,41	3
4	14382,83	25,11	3,9542	4,2581	16,95	4
5	14368,1	24,29	3,9711	4,2703	16,85	5
6	14175,37	24,79	4,069	4,3648	17,19	1
7	14149,59	25,31	4,0598	4,3632	17,03	2
8	13910,34	25,63	4,0746	4,4158	16,78	3
9	13765,02	26,83	4,0823	4,4518	16,73	4
10	13759,43	27,21	4,0512	4,4052	16,78	5

Z pośród zmiennych kandydatek dobieramy zmienne objaśniające stosując metodę Hellwiga.

Aby dobrać zmienne objaśniające potrzebny jest nam współczynnik korelacji. Wektor współczynnika korelacji - R₀ - obliczany za pomocą Współczynnika Pearsona.

r =	n(∑YX) - ∑Y * ∑X
		∑[n∑Y^2 - (∑X)^2] * [n∑X^2 - (∑X)^2]

Korzystając ze Współczynnika Pearsona otrzymaliśmy współczynnik korelacji pomiędzy zmienną objaśnianą a zmiennymi objaśniającymi (Ro) i współczynnik korelacji pomiędzy zmiennymi objaśniającymi (R):

Ro =	┌-0,91┐		R =	┌ 1	0,31	0,74	-0,68	0,45┐
		│-0,44│				│ 0,31	1	0,79	0,19	-0,3│
		│-0,86│				│ 0,74	0,79	1	-0,39	0,06│
		│ 0,76│				│ - 0,68	0,19	-0,39	1	-0,64│
		└-0,41┘				└ 0,45	-0,3	0,06	-0,64	1┘

Obliczając indywidualne i integralne nośniki pojemności informacji wybieramy zmienne objaśniające, które mają największy wpływ na kształtowanie się WIG - u.

nr.	zmienne					indywidualne					integ.
1	1					0,83					0,8288
2	2					0,20					0,1970
3	3					0,74					0,7398
4	4					0,58					0,5818
5	5					0,17					0,1652
6	1	2				0,63	0,15				0,7803
7	1	3				0,48	0,42				0,8992
8	1	4				0,49	0,35				0,8378
9	1	5				0,57	0,11				0,6870
10	2	3				0,11	0,41				0,5221
11	2	4				0,17	0,49				0,6549
12	2	5				0,15	0,13				0,2782
13	3	4				0,53	0,42				0,9505
14	3	5				0,70	0,16				0,8560
15	4	5				0,36	0,10				0,4563
16	1	2	3			0,40	0,09	0,29			0,7874
17	1	2	4			0,41	0,13	0,31			0,8564
18	1	2	5			0,47	0,12	0,09			0,6869
19	1	3	4			0,34	0,35	0,28			0,9684
20	1	3	5			0,38	0,41	0,11			0,8987
21	1	4	5			0,39	0,25	0,08			0,7190
22	2	3	4			0,10	0,34	0,37			0,8062
23	2	3	5			0,09	0,40	0,12			0,6151
24	2	4	5			0,13	0,32	0,09			0,5359
25	3	4	5			0,51	0,29	0,10			0,8955
26	1	2	3	4		0,30	0,09	0,25	0,26		0,8975
27	1	2	3	5		0,33	0,08	0,28	0,09		0,7889
28	1	2	4	5		0,34	0,11	0,23	0,07		0,7491
29	1	3	4	5		0,29	0,34	0,21	0,08		0,9175
30	1	2	3	4	5	0,26	0,08	0,25	0,20	0,07	0,8515

Największy wpływ na kształtowanie się WIG - u mają: cena 1 baryłki ropy, kurs euro w stosunku do złotego oraz średni kurs akcji w notowaniach ciągłych PKN Orlen.

	WIG	Ropa	Euro	PKN Orlen
t	Y	X1	X2	X3
1	14503,33	24,75	4,2981	17,21
2	14495,96	24,50	4,3231	17,56
3	14451,56	24,40	4,3428	17,41
4	14382,83	25,11	4,2581	16,95
5	14368,10	24,29	4,2703	16,85
6	14175,37	24,79	4,3648	17,19
7	14149,59	25,31	4,3632	17,03
8	13910,34	25,63	4,4158	16,78
9	13765,02	26,83	4,4518	16,73
10	13759,43	27,21	4,4052	16,78

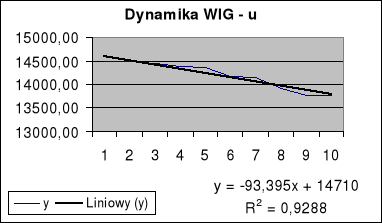
Z wykresu wynika, że badany model będzie miał postać liniową:

y_t = α₀ + α₁x_1t + α₂ x_2t + α₃x_3t + u_t

Wprowadzając symbolikę macierzową otrzymujemy:

Y =	┌14503,33┐	X =	┌1	24,75	4,2981	17,21┐
			│14495,96│		│1	24,50	4,3231	17,56│
			│14451,56│		│1	24,40	4,3428	17,41│
			│14382,83│		│1	25,11	4,2581	16,95│
			│14368,10│		│1	24,29	4,2703	16,85│
			│14175,37│		│1	24,79	4,3648	17,19│
			│14149,59│		│1	25,31	4,3632	17,03│
			│13910,34│		│1	25,63	4,4158	16,78│
			│13765,02│		│1	26,83	4,4518	16,73│
			└13759,43┘		└1	27,21	4,4052	16,78┘

┌	1	1	1	1	1	1	1	1	1	1┐
X^T =│	24,75	24,5	24,4	25,11	24,3	24,79	25,31	25,63	26,83	27,21│
│	4,2981	4,3231	4,34	4,258	4,27	4,3648	4,3632	4,4158	4,4518	4,4052│
└	17,2125	17,5625	17,4	16,95	16,9	17,1875	17,025	16,775	16,725	16,775┘

Mnożąc macierze otrzymujemy:

┌	10,00	252,82	43,49	170,48┐			┌	141961,53┐
X^T * X = │	252,82	6400,96	1100,02	4308,16│			X^T * Y =│	3586645,65│
│	43,49	1100,02	189,20	741,39│			│	617291,69│
└	170,48	4308,16	741,39	2906,92┘			└	2420669,40┘

Odwracając macierz X^T * X otrzymujemy:

┌		1569,26	-5,84	-136,43	-48,58┐
(X^T* X)^-1 = │		-5,84	0,41	-3,70	0,67│
│		-136,43	-3,70	65,49	-3,22│
└		-48,58	0,67	-3,22	2,67┘
Szacujemy wektor ocen parametrów strukturalnych modelu:
┌	19884,86┐
αˆ = │	-79,58│
│	-2349,71│
└	383,80┘

Oszacowany model ekonometryczny ma postać:

y^ = 19884,86 - 79,58x_1t - 2349,71x_2t + 383,80x_3t

Jeżeli cena za 1 baryłkę ropy, kurs euro w stosunku do złotego i kurs średni w notowaniach ciągłych akcji PKN Orlen będą równe 0, to WIG wyniesie 19884,86 pkt.

Jeżeli cena za 1 baryłkę ropy wzrośnie o 1 dolara (a pozostałe zmienne nie ulegną zmianie) to WIG spadnie o 79,58 pkt.

Jeżeli kurs euro w stosunku do złotego wzrośnie o jednostkę (a pozostałe zmienne nie ulegną zmianie) to WIG spadnie o 2349,71 pkt.

Jeżeli kurs średni w notowaniach ciągłych akcji PKN Orlen wzrośnie o złotówkę (a pozostałe zmienne nie ulegną zmianie) to WIG wzrośnie o 383,80 pkt.

Wyznaczamy wektor teoretycznych wartości zmiennej objaśnianej oraz wektor reszt:

Yˆ = X * αˆ =	┌14422,17┐	Y =	┌14503,33┐	Y - Yˆ = e =	┌ 81,16┐
			│14517,65│			│14495,96│		│ -21,69│
			│14421,74│			│14451,56│		│ 29,82│
			│14386,76│			│14382,83│		│ -3,93│
			│14384,97│			│14368,10│		│ -16,87│
			│14252,66│			│14175,37│		│ -77,29│
			│14152,68│			│14149,59│		│ -3,09│
			│13907,67│			│13910,34│		│ 2,67│
			│13708,40│			│13765,02│		│ 56,62│
			└13806,84┘			└13759,43┘		└ -47,41┘

e^T =

[81,16

-21,69

29,82

-3,93

-16,87

-77,29

-3,09

2,67

56,62

-47,41]

Szacujemy wariację odchyleń losowych na podstawie wzoru:

Se^2 =	e^T * e	= 3281,97
			n-k
Se	= 57,29

Rzeczywista wartość WIG - u różni się średnio o ± 57,29 pkt. na dzień od wartości teoretycznych obliczonych na podstawie modelu.

Obliczy współczynnik zbieżności według wzoru:

φ^2 =	(n - k) * Se^2
		∑(yt - y^¯)^2

Y	Y - Y^¯	(Y - Y^¯)^2
14503,33	307,18	94357,71
14495,96	299,81	89884,24
14451,56	255,41	65232,74
14382,83	186,68	34848,30
14368,10	171,95	29565,77
14175,37	-20,78	431,93
14149,59	-46,56	2168,11
13910,34	-285,81	81689,07
13765,02	-431,13	185875,66
13759,43	-436,72	190726,98
141961,53	0,00	774780,51

φ^2 =	19691,83	= 0,025
			774780,51

W 2,5% zmienność WIG - u nie była wyjaśniona cenę baryłki ropy, kursem euro i kursem akcji PKN Orlen.

Współczynnik determinacji:

R² = 1 - 0,025 = 0,975

W 97,5% zmienność WIG - u była wyjaśniona cenę baryłki ropy, kursem euro i kursem akcji PKN Orlen.

Współczynnik zmienności losowej obliczamy jako:

Vs =	Se	=	57,29	= 0,004
			Y_			14196,15

W modelu odchylenie losowe stanowi 0,4% średniej wartości WIG - u. Badany model jest bardzo dobrze dopasowany do danych rzeczywistych.

Obliczamy błędy średnich szacunku parametru:

D^2(αˆ) = Se^2* (X^T* X)^-1 =		3281,97 *	┌1569,26	-5,84	-136,43	-48,58┐
						│ -5,84	0,41	-3,70	0,67│
						│-136,43	-3,70	65,49	-3,22│
						└ -48,58	0,67	-3,22	2,67┘
D^2(αˆ) =	┌5150278,53	-19169,69	-447765,79	-159426,64┐
		│ -19169,69	1358,70	-12143,06	2207,55│
		│ -447765,79	-12143,06	214922,06	-10558,63│
		└ -159426,64	2207,55	-10558,63	8771,86┘
D(αˆ0) =	2269,42
D(αˆ1) =	36,86
D(αˆ2) =	463,60
D(αˆ3) =	93,66

Szacowany model wraz z błędami ocen parametrów można zapisać następująco:

y^ = 19884,86 - 79,58x_1t - 2349,71x_2t + 383,80x_3t

^{(2269,42) (36,86) (463,60) (93,66)}

Jeżeli cena za 1 baryłkę ropy, kurs euro w stosunku do złotego i kurs średni w notowaniach ciągłych akcji PKN Orlen będą równe 0 to WIG wyniesie 19884,86 pkt., przy szacowaniu tego parametru mylimy się średnio ± 2269,42 pkt.

Jeżeli cena za 1 baryłkę ropy wzrośnie o 1 dolara (a pozostałe zmienne nie ulegną zmianie) to WIG spadnie o 79,58 pkt., przy szacowaniu tego parametru mylimy się średnio ± 36,86 pkt.

Jeżeli kurs euro w stosunku do złotego wzrośnie o jednostkę (a pozostałe zmienne nie ulegną zmianie) to WIG spadnie o 2349,71 pkt., przy szacowaniu tego parametru mylimy się średnio ± 463,60 pkt.

Jeżeli kurs średni w notowaniach ciągłych akcji PKN Orlen wzrośnie o złotówkę (a pozostałe zmienne nie ulegną zmianie) to WIG wzrośnie o 383,80 pkt., przy szacowaniu tego parametru mylimy się średnio ± 93,66 pkt.

Test serii:

Reszty U_t ≥ 0 oznaczamy A,

Reszty U_t < 0 oznaczamy B.

Reszty seria

307,18 A

299,81 A

255,41 A

186,68 A

171,95 A

-20,78 B

-46,56 B

-285,81 B

-431,13 B

-436,72 B

H₀: rozkład reszt dodatnich i ujemnych jest losowy

H₁: rozkład reszt dodatnich i ujemnych nie jest losowy

Liczymy maksymalną długość serii z A lub B i oznaczamy przez K (liczba elementów w najdłuższej serii). Jeżeli liczba serii (K) zawiera się pomiędzy wartościami krytycznymi odczytanymi z tablicy rozkładu liczby serii to odchylenia losowe są losowe. Jeżeli tak nie jest to nie są losowe. Poziom istotności przy teście dwustronnym wynosi 0,05

K = 5

Wartości krytyczne odczytanymi z tablicy rozkładu liczby serii dla dwustronnego obszaru krytycznego wynoszą (2 , 9)

Jeżeli liczba serii (K) zawiera się pomiędzy wartościami krytycznymi, więc nie ma podstaw do odrzucenia H₀, rozkład reszt jest losowy.

Badanie istotności wpływu poszczególnych zmiennych objaśniających na zmienną objaśnianą:

H₀: α_i = 0

H₁: α_i ≠ 0

tαo	8,76
tα1	-2,16
tα2	-5,07
tα3	4,10

Wszystkie parametry są większe od 2, dlatego odrzucamy H_o na rzecz H₁, a więc parametry te są istotne statystycznie.

Badanie autokorelacji składników losowych:

H₀: brak autokorelacji

H₁: jest autokorelacja

et	et-1	et - et-1	(et - et-1) ^2	et^2
81,16	"-"			6587,57
-21,69	102,85	-124,54	15509,29	470,29
29,82	-51,50	81,32	6612,37	888,94
-3,93	33,75	-37,68	1419,52	15,45
-16,87	12,94	-29,80	888,18	284,48
-77,29	60,43	-137,72	18966,26	5974,10
-3,09	-74,21	71,12	5058,26	9,52
2,67	-5,76	8,43	71,09	7,15
56,62	-53,95	110,57	12226,57	3206,21
-47,41	104,04	-151,45	22937,73	2248,12
suma			83689,26	19691,83

d =	19691,83	= 0,2353
			83689,3

Według statystyki Durbini - Wadsona otrzymaliśmy autokorelację dodatnią czyli d < 2. weryfikując otrzymaną autokorelację z wartościami krytycznymi d_L = 0,697; d_U = 1,641 odczytanymi z tablicy Durbini - Wadsona odrzucamy H₀ na rzecz H₁, a więc występuje autokorelacja dodatnia .

Po przeprowadzonym kompleksowych badań możemy stwierdzić ma podstawie otrzymanych wyników, iż cena za 1 baryłkę ropy, kurs euro w stosunku do złotego i kurs średni w notowaniach ciągłych akcji PKN Orlen mają duży wpływ na kształtowanie się Warszawskiego Indeksu Giełdowego w badanym przedziale czasowym.

Praca pochodzi z serwisu www.e-sciagi.pl

1

---