40mm/dobe - 40 litrow na m2 na dobe

1m3 = 1000l

0,07 m3/dobe = 0,07/24 m3/h = 70/3600 l/s

0,07 m3 = 70l

150 mm/lipiec = 0,15/31 m3/dobe = 0,15/31*24*3600 m3/h

Obliczanie wskaźnika opadów (sredni roczny opad) i wielkość infiltracji

P = [(∑ Pn+Pn₁/2) *An] / ∑ An

Pn - opad w poszczególnych stacjach pomiarowych [mm],

An - pole powierzchni poszczególnych wieloboków [cm2 , km2]

Wskaźnik infiltracji to chyba 0,2 ?

1. wzór Hazena: k = C * d₁₀² [m/d]

2. wzór USBSC (amerykański):

k = 0,36 . D₂₀^2,3 [cm/s], dla Twody = 10^oC

U - współczynnik nierównomierności uziarnienia: U = d60/d10,

C - empiryczny współczynnik zależny od nierównomierności uziarnienia wg Langego:

C = 400 + 40 (n-26), gdzie n - współczynnik porowatości w [%], przyjąć 30 [%] ().

Q = k . I . A; [m3/s]

k - współczynnik filtracji (wodoprzepuszczalności) [m/s]

I - spadek hydrauliczny (gradient hydrauliczny) I= delta H / L

A - powierzchnia przekroju strumienia [m2].

Spadek hydrauliczny to różnica naporów ၄H = H1 - H2 odniesiona do długości drogi L, na której ona wystąpiła

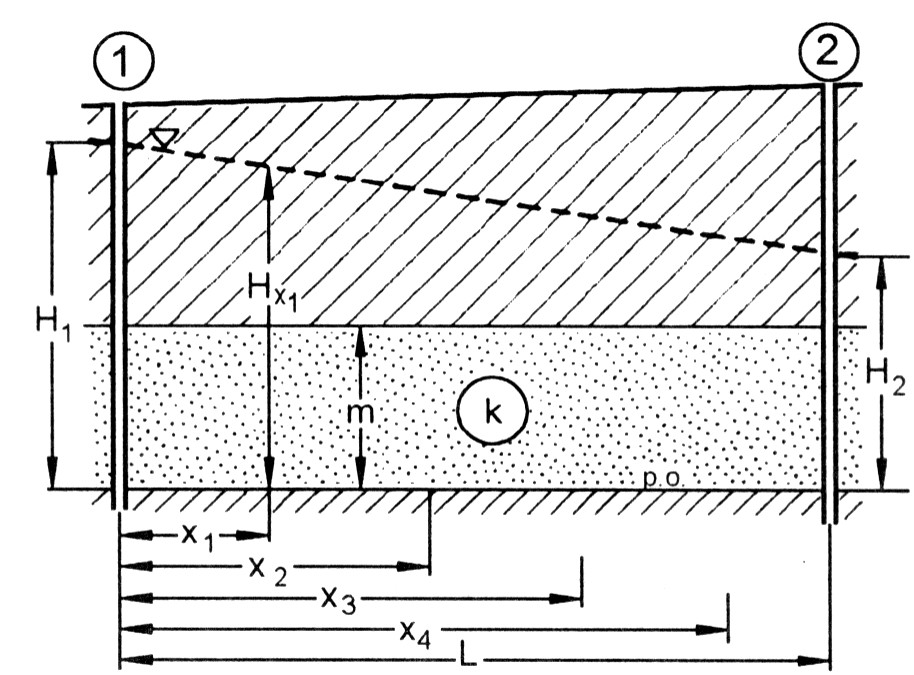
Zadanie o zwierciadle naporowym lub swobodnym plus rysunki

k = 10 [m/d] L = 900[m] m = 25 [m] rt1 = 315 [m n.p.m] rt2 = 317 [m n.p.m] gzw1 = 7[m p.p.t.] gzw2 = 18 [m p.p.t.] Hp = 255 [m n.p.m]

chyba szykane q, Q700, H200, H400, H600, H800

wzory do tego zadania: o zwierciadle naporowym

H1=Rt1 - gzw1 H2=Rt2 - gzw2

Potem liczy się
np. Q700 = q . 700[m]

Następnie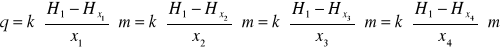

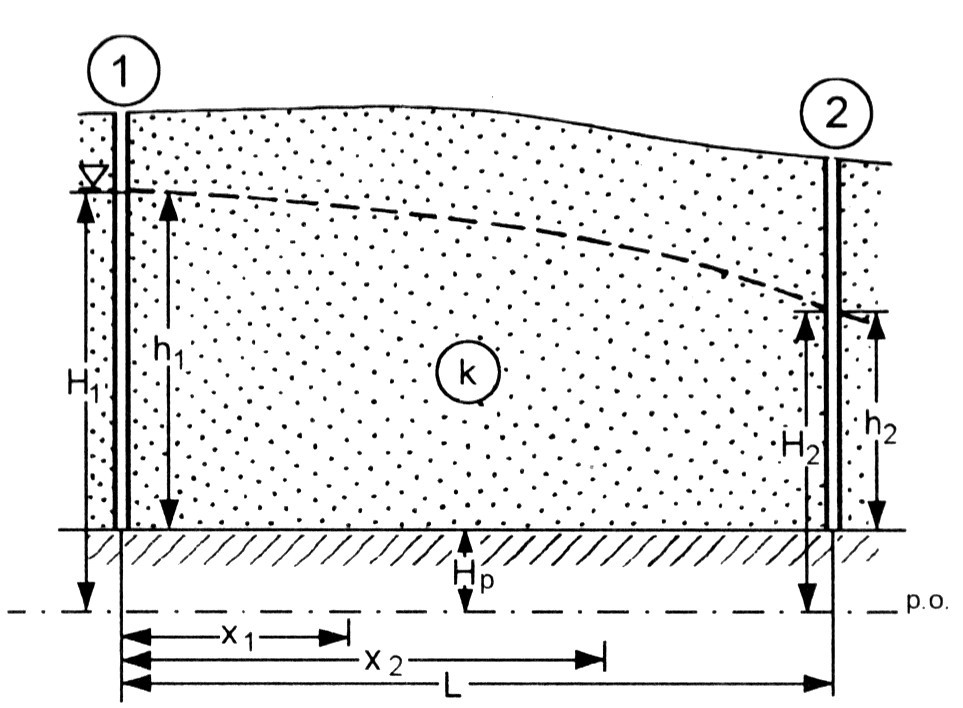
A teraz zadanie o swobodnym zwierciadle

Dane: k = 10 [m/d], Hp = 96,0 [m n.p.m]. H1 = 125 [m n.p.m.] H2 = 119 [m n.p.m.] L = 380 [m] B = 2 500 [m]
Szukane: q, Q2500, H120, H260

q = k ∙ J ∙ mśr

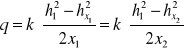
Cos o jakiejs migracji

Q = k . I . A; [m3/s] lub

gdzie: v - prędkość filtracji [m/s; m/h; m/d; m/a]

vr - średnia rzeczywista prędkość przepływu wód podziemnych [m/s; m/h; m/d; m/a]

Czas (t) migracji substancji zachowawczej (konserwatywnej) t=L/v_r

Czas (ts) migracji substancji ulegającej sorpcji t_s = R . t

ZADANIE o USTALONYM DOPŁYWIE WODY DO STUDNI ZUPEŁNEJ

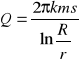
lub

gdzie: Q - wydajność pompowania [m3/h], k - współczynnik filtracji [m/h], m - miąższość warstwy wodonośnej [m], H-ho = s - depresja w studni [m], H - wysokość statycznego zwierciadła wody [m],ho- wysokość dynamicznego zwierciadła wody w studni [m] r - promień studni [m], R - promień leja depresji [m]:
wzór Sichardta(dla k w [m/d])

ZADANIE

Otwór wiertniczy o średnicy d = 305 mm przewiercił warstwę glin morenowych o miąższości m' = 18 m, a następnie warstwę piaszczysto-żwirową tworzącą naporowy poziom wodonośny. Miąższość warstwy wodonośnej m = 17,5 m, zaś współczynnik filtracji k = 19,8 m/d. Zwierciadło statyczne wody w otworze ustaliło się na głębokości g = 3,7 m p.p.t.

Określić:

• wydatek studni „Q” przy obniżeniu w niej poziomu zwierciadła wody

o s = 8 m;

- wydatek jednostkowy otworu „q”.

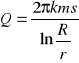
[m3/h] H = m + m'- g [m]

[m] dla k w [m/d] to wzor dla swobodnych

a taki tylko ze ma być dzielone przed pierwiastkiem dla naporowych

[m3/h/1ms]

H = gstr - gzw [m]; ho = H - s [m]

---