Estymacja przedziałowa parametrów strukturalnych zbiorowości generalnej

Parametr zbiorowości generalnej
- miara opisowa, np. średnia arytmetyczna
odchylenie standardowe
czy wskaźnik struktury
zbiorowości generalnej, której wartość jest na ogół nie znana.

Estymacja, czyli szacowanie parametrów, polega na podaniu ocen parametrów populacji generalnej na podstawie statystyki uzyskanej z próby losowej.

Statystyki wyliczone na podstawie pobranych z populacji grup losowych z teorii estymacji noszą nazwę estymatorów. Estymatorem jest więc każda statystyka wyliczona z próby losowej, która służy do szacowania odpowiadającego jej parametru populacji generalnej.

Aby statystyki mogły być uznane za dobre estymatory powinny charakteryzować się pewnymi cechami:

1. Nieobciążoność - jeśli wartość oczekiwana estymatora stosowanego do wyznaczenia nieznanego parametru zbiorowości generalnej jest równa wartości tego parametru, to taki estymator nazywamy nieobciążonym:

2. Zgodność - własność estymatora powodująca, że wraz ze wzrostem liczebności próby wartość estymatora zbliża się do parametru zbiorowości generalnej. Innymi słowy różnica między tymi wielkościami podlega działaniu prawa wielkich liczb:

gdzie:

jest dowolnie małą liczbą

3. Efektywność - spośród dwóch estymatorów wybieramy ten, którego wariancja jest mniejsza. Miarą efektywności estymatora jest jego wariancja
   .

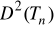
Wyróżniamy dwa rodzaje estymacji:

1. Estymacja punktowa polega na podaniu wielkości szacowanego parametru, która jest równa wartości estymatora. Ponieważ z reguły wielkości estymatora różnią się od wartości parametru populacji generalnej, podaje się jednocześnie średni błąd szacunku, czyli odchylenie standardowe estymatora.

2. Estymacja przedziałowa polega na skonstruowaniu pewnego przedziału liczbowego, zwanego przedziałem ufności (Neymana), który z określonym prawdopodobieństwem pokryje estymarowy parametr.

Losowanie niezależne (ze zwrotem) - proces wybory jednostek do próby, w którym każdorazowo elementy zbiorowości generalnej mają takie samo prawdopodobieństwo dostania się do próby.

Rozkład estymatora w próbie - rozkład prawdopodobieństwa wskazujący na wszystkie możliwe wielkości, jakie może przyjąć dana statystyka (np. średnia arytmetyczna w próbie, odchylenie standardowe w próbie czy częstość względna w próbie).

Błąd standardowy - odchylenie standardowe estymatora
, które zapisujemy
.

Zbieżność do rozkładu normalnego - jeśli liczba jednostek obserwacji dąży do nieskończoności (w praktyce oznacza to zazwyczaj
), to rozkład estymatora
jest zbliżony do rozkładu normalnego.

Wartość oczekiwana średniej arytmetycznej z próby

gdzie:

- wartość średniej w zbiorowości generalnej,

- wartość średniej w próbie.

Błąd standardowy średniej arytmetycznej z próby

Wartość oczekiwana wskaźnika struktury z próby

gdzie:

- nieznana wartość wskaźnika struktury (częstości względnej) zbiorowości generalnej

Błąd standardowy wskaźnika struktury z próby

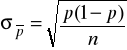
gdzie:

- nieznana wartość wskaźnika struktury z próby

Estymacja przedziałowa nieznanej wartości średniej populacji generalnej

Współczynnik ufności - dzięki estymacji przedziałowej wyznacza się przedział liczbowy, który z pewnym prawdopodobieństwem zawiera nieznaną wartość parametru. To prawdopodobieństwo nazywane jest współczynnikiem ufności, a oszacowany przedział - przedziałem ufności (Neymana).

Współczynnik ufności oznacza się:
. Najczęściej ma on takie wartości:

0,99 0,95 0,90

2,58 1,96 1,64

Przedział ufności Neymana ma postać ogólną:

gdzie:

- wartość zmiennej losowej w rozkładzie
, takiej że

lub następującą formułę:

gdzie:

- wartość zmiennej losowej w rozkładzie t-Studenta przy
stopniach swobody, takiej że prawdopodobieństwo
.

Zbieżność rozkładu średniej z próby
do rozkładu normalnego - wraz ze wzrostem liczby jednostek w próbie
estymator
ma rozkład zbliżony do rozkładu normalnego o nadziei matematycznej (wartości oczekiwanej) równej
i odchyleniu standardowym
. Jest to szczególny przypadek działania prawa wielkich liczb.

Normalność rozkładu średniej z prób
- jeśli zmienna losowa X ma rozkład normalny, to także x ma rozkład normalny, bez względu na wielkość próby.

Zbieżność do rozkładu t-Studenta - gdy nie jest możliwe skorzystanie ze zbieżności rozkładu
do rozkładu normalnego, zmienna X w zbiorowości generalnej ma rozkład normalny oraz nieznane jest
z populacji generalnej, wówczas korzystamy ze zbieżności statystyki
do rozkładu t-Studenta o
stopniach swobody, gdzie
w zależności od liczebności próby
(odpowiednio
).

Sposób budowy przedziałów ufności dla
w zależności od informacji pochodzących ze zbiorowości generalnej, rozkładu statystyki
oraz wielkości próby przedstawia schemat.

tak nie

tak nie

1)

1) 2)

Objaśnienie do powyższego schematu:

Schemat ten przedstawia przedziały ufności dla nieznanej wartości średniej (
) zmiennej X o rozkładzie normalnym lub zbliżonym do normalnego

1)
to wartość
o rozkładzie
taka że

2)
to wartość
o rozkładzie t-Studenta o
stopniach swobody, która spełnia zależność

Przykład 10

(na przedział ufności dla wartości oczekiwanej)

W pewnym zakładzie produkcyjnym postanowiono zbadać staż pracy pracowników umysłowych. W tym celu z populacji tych pracowników wylosowano grupę (losowanie niezależne (ze zwrotem)) o liczbie
pracowników, z której obliczono średnią
lat. Dotychczasowe doświadczenie wskazuje, że rozkład stażu pracowników umysłowych jest rozkładem normalnym z odchyleniem standardowym 2,8 lat (
).

Przyjmując współczynnik ufności
zbudować przedział ufności dla nieznanego średniego stażu pracy w populacji pracowników umysłowych w tym zakładzie.

Zgodnie ze schematem ustalamy, że spełnione są warunki:

- odchylenie standardowe

- rozkład normalny

Zatem korzystamy z następującego wzoru na przedział ufności dla nieznanej wartości
ze zbiorowości generalnej:

Na podstawie tablic dystrybuanty rozkładu normalnego dla

wiemy, że

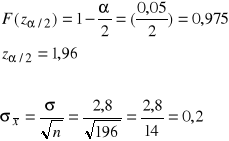
Przedział ufności przyjmuje postać:

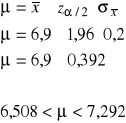
Odp.: Z prawdopodobieństwem 0,95 możemy przypuszczać, że średni staż pracy w populacji pracowników umysłowych w tym zakładzie zawiera się w przedziale (6,508 lat; 7,292 lat). Innymi słowy 95% wszystkich takich przedziałów pokryje parametr
, natomiast 5% nie pokryje. Godzimy się więc z ryzykiem błędu, że w 5 przypadkach na 100 nieznana wartość średniego stażu pracy w populacji generalnej znajduje się poza wyznaczonym przedziałem liczbowym.

Wykreślenie graficzne f(z)

0

Przykład 11

Odchylenie standardowe

W losowo wybranej grupie 450 samochodów osobowych marki FSO 1500 przeprowadzono badanie zużycia benzyny na tej samej dla wszystkich samochodów trasie długości 100 km. Okazało się, że odchylenie standardowe zużycia benzyny dla tej grupy samochodów wynosiło 0,8 litra na 100 km.

Zakładając, że badana cecha ma rozkład normalny wyznaczyć przedział ufności dla odchylenia standardowego ze zużyciem benzyny przez wszystkie samochody tej marki na takiej trasie. Przyjąć współczynnik ufności 0,99.

Rozwiązanie

S = 0,8 (odchylenie standardowe)

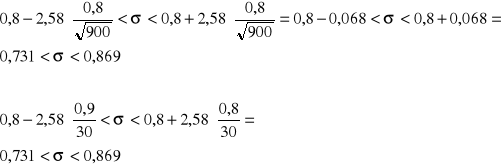
Odp.: Otrzymany przedział 0,731 i 0,869 jest jednym z tych wszystkich możliwych do otrzymania przedziałów, które z prawdopodobieństwem 0,99 pokrywają odchylenie standardowe zużycia benzyny przez samochody FSO 1500 na trasie 100 km.

Przykład 12

W celu oszacowania średniej długości pewnego detalu produkowanego w przedsiębiorstwie wylosowano 17 detali i otrzymano średnią ich długość 32 cm oraz odchylenie standardowe 0,6 mm.

Oszacować przy współczynniku ufności 0,90 wartość oczekiwaną produkowanych w tej firmie detali.

Rozwiązanie

Rozkład t-Studenta

Rozwiązaniem jest przedział liczbowy dla nieznanej
, który wyznaczymy ze schematu przy założeniu, że x zbiorowości generalnej ma rozkład normalny.

Z tablic rozkładu t-Studenta otrzymujemy dla liczby stopnia
, który u nas równa się
i

Skorzystamy ze wzoru:

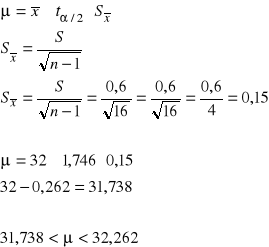
Odp.: W 90% możemy przypuszczać, że w przedziale od 31,738 do 32,262 produkuje się średnią długość detali w tym przedsiębiorstwie.

Wykres graficzny

f(t)

0
t

Graficzna ilustracja

Estymacja przedziałowa nieznanego wskaźnika struktury zbiorowości generalnej

Estymatorem wskaźnika struktury frakcji (prawdopodobieństwa) jest wskaźnik struktury z próby losowej.

Warunkiem często zalecanym w procederze szacowania wskaźnika struktury
jest duża próba
. W zastosowaniach statystyki warunek ten jest znacznie łagodniejszy
. Oczywiście, im większa próba, tym bardziej precyzyjne wyniki.

Błąd standardowy estymatora

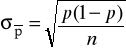
Przedział ufności dla nieznanego wskaźnika struktury zbiorowości generalnej (p)

gdzie:

- wartość zmiennej losowej standaryzowanej w rozkładzie normalnym, przy danym
, gdyż mamy zawsze do czynienia z dużą próbą.

Przedział ufności dla
(rząd wielkości
nie jest znany)

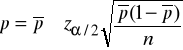
Przykład 12

Chcemy znaleźć prawdopodobieństwo tego, że losowo wybrany pracownik pewnego dużego zakładu będzie miał wykształcenie wyższe. W tym celu wylosowano próbę liczącą 400 pracowników i stwierdzono, że 32 spośród nich posiada wykształcenie wyższe.

Oszacować na tej podstawie przy współczynniku ufności 0,95 udział osób z wykształceniem wyższym spośród zatrudnionych w tym przedsiębiorstwie.

Rozwiązanie zadania

p - wskaźnik struktury

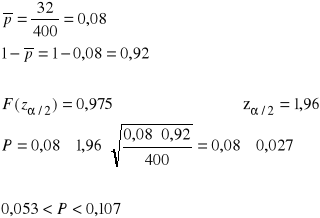
Odp.: Z 95% wiarygodnością możemy przypuszczać, że odsetek osób z wykształceniem wyższym w tym przedsiębiorstwie waha się w przedziale od 5,3% do 10,7%.

Można niekiedy zastosować najostrożniejszy sposób postępowania. Polega on na przyjęciu maksymalnej wartości
:

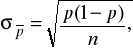
przy danym
osiąga maksimum dla

Przedział ufności dla
(najostrożniejszy sposób postępowania przy danym

Niezbędna (minimalna) liczebność próby w przypadku szacowania p (wskaźnika struktury)

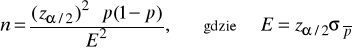
Gdy
nie jest wstępnie znane (np. brak badań pilotażowych czy innych wcześniejszych informacji), wówczas można przyjąć:

Zatem wzór na niezbędną liczebność próby przyjmuje następującą postać:

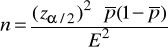
lub przy postępowaniu w najostrożniejszy sposób

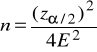
gdzie:

- bezwzględny maksymalny błąd szacunku

Przykład 13

Właściciel sklepu z artykułami żywnościowymi chce ustalić procent swoich stałych klientów spośród ogółu klientów jego sklepu. Jak liczną grupę powinien wylosować, aby z prawdopodobieństwem 95% maksymalny błąd szacunku nie przekraczał 5%?

Rozwiązanie:

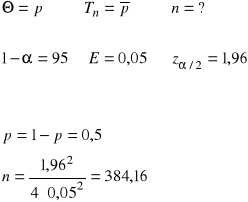
Skorzystaliśmy z tego właśnie wzoru, gdyż brak jest jakichkolwiek informacji o odsetku klientów powtarzających zakupy w tym sklepie (to chcieliśmy właśnie ustalić), zatem postąpiliśmy w sposób najostrożniejszy.

Odp.: Należy zatem wylosować próbę liczącą 385 klientów.

σ znane

ma rozkład zbliżony

do t-Studenta o n-1

stopnia swobody

ma rozkład normalny lub

asymptotycznie normalny o

parametrach
i

---