Wnioskowanie statystyczne to proces myślowy polegający na formułowaniu sądów o całości przy dysponowaniu o niej ograniczoną liczbą informacji.
Zmienna losowa skokowa i jej rozkład
Zmienną losową X jest wielkość, która przy zajściu każdego zdarzenia losowego ω przyjmuje konkretną wartość ![]()
, co można zapisać w sposób następujący:
![]()
Innymi słowy zmienna losowa X jest liczbową prezentacją wyniku doświadczenia losowego, a więc jej wartość zależna jest od przypadku.
Jeśli doświadczenie polega na kontroli jakości 20 komputerów wyprodukowanych przez producenta tych wyrobów, to zmienną losową X będzie liczba wadliwych komputerów, która może przyjąć wartości: od 0 do 20. Jeśli poszczególnym wartościom ![]()
przyporządkujemy prawdopodobieństwa realizacji tej zmiennej losowej oznaczonej przez ![]()
, wówczas otrzymamy rozkład prawdopodobieństwa zmiennej losowej skokowej, przy czym: ![]()
Znać rozkład zmiennej losowej skokowej X to znać realizacje tej zmiennej, czyli ![]()
, oraz odpowiadające im prawdopodobieństwa ![]()
.Rozkład zmiennej losowej skokowej można przedstawić za pomocą funkcji prawdopodobieństwa zmiennej losowej skokowej lub tablicy.
Przykładem zmiennej losowej skokowej jest wielkość popytu na określone dobro. Popyt zależy bowiem od wielu czynników, takich jak: ceny dobra, ceny innych dóbr (substytucyjnych), dochód do dyspozycji gospodarstwa domowego zgłaszającego popyt na to dobro itp. Jest zatem, przynajmniej częściowo, zależny od przypadku.
Wartość oczekiwana zmiennej losowej skokowej![]()
Wartość oczekiwana jest zatem średnią arytmetyczną ważoną realizacji ![]()
zmiennej losowej X, a wagami są odpowiadające im prawdopodobieństwa ![]()
.
Wariancja zmiennej losowej skokowej ![]()
Odchylenie standardowej zmiennej losowej skokowej
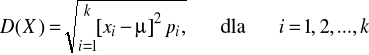
![]()
Dystrybuanta zmiennej losowej ![]()
nazywa się prawdopodobieństwem tego, że zmienna losowa przyjmie wartości mniejsze lub równe określonej wartości ![]()
(czyli jest równa sumie prawdopodobieństw realizacji wartości zmiennej, mniejszych bądź równych ![]()
). Jest to funkcja określana wzorem:![]()
Dystrybuanta zmiennej losowej skokowej (dyskretnej) ![]()
Ważniejsze teoretyczne rozkłady zmiennej losowej skokowej
Zmienna losowa X ma rozkład zero-jedynkowy, jeżeli jej funkcja prawdopodobieństwa (rozkład) jest następująca:![]()
![]()
Wartość oczekiwana i wariancja w tym rozkładzie wynoszą:
![]()
Zmienna losowa X ma rozkład dwumianowy (Bernoulliego)![]()
, jeśli jej funkcja prawdopodobieństwa określona jest wzorem:
![]()
,
gdzie:
![]()
- liczba wariantów zmiennej losowej,
![]()
- liczba realizacji zdarzenia ![]()
,
![]()
- prawdopodobieństwo realizacji zdarzeń ![]()
w każdej z niezależnych realizacji.
Wartość oczekiwana w tym rozkładzie wynosi: ![]()
a wariancja: ![]()
Schemat Bernoulliego:
Z takim rozkładem mamy do czynienia w przypadku wyznaczania prawdopodobieństwa kolejnych wartości ![]()
w ![]()
doświadczeniach. Aby rozkład dwumianowy mógł znaleźć zastosowanie, muszą być spełnione następujące warunki:
przeprowadza się
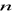
jednakowych doświadczeń,dla każdego doświadczenia możliwe są dwa wyniki: jeden - zwany sukcesem, a drugi porażką,
prawdopodobieństwo sukcesu
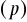
czy porażki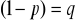
w kolejnych doświadczeniach jest stałe,doświadczenia są od siebie niezależne.
Rozkład Poissona dotyczy zmiennej losowej skokowej. Znajduje on zastosowanie w sytuacjach, gdy próba jest liczna ![]()
oraz gdy prawdopodobieństwo zajścia sukcesu jest małe (co najwyżej kilkuprocentowe). Jego przydatność jest duża, np. w ustalaniu prawdopodobieństwa wadliwości produkcji czy awaryjności maszyn.
Prawdopodobieństwo w rozkładzie Poissona ![]()
gdzie:![]()
- średnia liczba zdarzeń,![]()
Rozkładem Poissona można przybliżyć rozkład dwumianowy, gdy spełnione są następujące warunki:
duża liczba doświadczeń
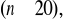
stały iloczyn

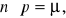
prawdopodobieństwo
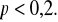
Rozkład normalny i inne rozkłady zmiennej losowej ciągłej
Zmienna losowa ciągła jest to taka zmienna, która przyjmuje wszystkie wartości z pewnego określonego przedziału liczbowego.
Zmienną losową ciągłą jest czas pracy przeznaczony na wyprodukowanie sztuki wyrobu przez pracowników pewnej fabryki, waha się on np. w przedziale od 3 do 5 godzin. Może zatem przyjąć dowolne wartości z tego przedziału, np. 3, 1; 4,23 itp.
Rozkład normalny to najważniejszy rozkład zmiennej losowej ciągłej. Odgrywa on w zastosowaniach statystyki ogromną rolę.
Zmienna losowa standaryzowana![]()
![]()
Rozkład chi-kwadrat ![]()
Zakładając, że ![]()
są niezależnymi zmiennymi losowymi o rozkładzie normalnym o parametrach ![]()
zmienna losowa ![]()
określona jest w sposób następujący:![]()
ma rozkład ![]()
z ![]()
„liczbą stopni swobody”.
Zmienna losowa o rozkładzie chi-kwadrat przyjmuje wartości dodatnie, a jej rozkład zależy od liczby stopni swobody ![]()
. Dla małych wartości ![]()
jest to rozkład silnie asymetryczny, w miarę wzrostu ![]()
asymetria jest coraz mniejsza: ![]()
wyznaczamy najczęściej jako: ![]()
gdzie: ![]()
- liczebność próby,
![]()
- liczba szacowanych parametrów z próby.
Wartość oczekiwana w rozkładzie ![]()
![]()
Wariancja w rozkładzie![]()
![]()
Odchylenie standardowe w rozkładzie ![]()
![]()
Rozkład t-Studenta
Wartość oczekiwana w rozkładzie t-Studenta ![]()
Wariancja w rozkładzie t-Studenta![]()
Odchylenie standardowe w rozkładzie t-Studenta 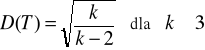
Wyszukiwarka
Podobne podstrony:
Finanse publiczne - pytania z egzaminu, Studia UE Katowice FiR, I stopień, semestr III, Finanse Publ
test 2011, Studia UE Katowice FiR, I stopień, semestr III, Finanse Publiczne
wykłady Famulska, Studia UE Katowice FiR, I stopień, semestr III, Finanse Publiczne
Partnerstwo Publiczno-prawne, Studia UE Katowice FiR, I stopień, semestr III, Finanse Publiczne
sciaga finanse, Studia UE Katowice FiR, I stopień, semestr III, Finanse Publiczne
wyklad 1 - wprowadzenie do prawoznawstwa, Studia UE Katowice FiR, I stopień, semestr I, Prawo Szpor
ściąga Zaip, Studia UE Katowice FiR, I stopień, semestr V, Zarządzanie Aktywami i Pasywami Banku
Ściąga - Bieniok, Studia UE Katowice FiR, I stopień, semestr I, Zarządzanie
zaliczenie+rzeszotarska, Studia UE Katowice FiR, I stopień, semestr II, Makroekonomia
Funkcje państwa, Studia UE Katowice FiR, I stopień, semestr II, Makroekonomia
4 niezależności Banku Centralnego, Studia UE Katowice FiR, I stopień, semestr II, Makroekonomia
wyklad 2 - prawo konstytucyjne, Studia UE Katowice FiR, I stopień, semestr I, Prawo Szpor
wyklad 3 - wolnosc, Studia UE Katowice FiR, I stopień, semestr I, Prawo Szpor
Test prawda-fałsz, Studia UE Katowice FiR, I stopień, semestr II, Finanse
Działalność banków inwestycyjnych na rynku wtórnym papierów wartościowych - tekst, Studia UE Katowic
więcej podobnych podstron