Wojskowa Akademia Techniczna

Im. Jarosława Dąbrowskiego

LABORATORIUM FIZYKI OGÓLNEJ

Sprawozdanie z ćwiczenia laboratoryjnego

Nr1

Tytuł: ROZKŁAD NORMALNY

Wykonał: Emilian Dudek Warszawa dn. 25.10.2004

Grupa szkoleniowa: E04D10

Prowadzący zajęcia: dr inż. W. Piecek

Ocena przygotowania do zajęć:………….

Ocena końcowa:………….

I. WSTĘP TEORETYCZNY

Celem ćwiczenia jest otrzymanie eksperymentalnego rozkładu Gaussa, naniesienie na nim odpowiedniego rozkładu ciągłego ciągłego i wyznaczenie parametrów tego rozkładu.

Układy fizyczne złożone z wielu identycznych elementów, które mogą przyjmować dwa lub więcej stanów w sposób niezależny nazywamy zespołami statystycznymi. Do opisu takich zespołów stosujemy procedury zwane rozkładami statystycznymi. Pozwalają one określić prawdopodobieństwo wystąpienia danej sytuacji w zespole.

1. Rozkład dwumienny

Rozważmy taki zespół statystyczny, w którym N elementów może przyjmować jeden z dwóch stanów. Określamy:

p - prawdopodobieństwo wystąpienia jednego stanu

q - prawdopodobieństwo wystąpienia drugiego stanu

n - ilość elementów przyjmujących pierwszy stan

Ilość sposobów, na które realizowana jest taka kombinacja elementów zespołu wynosi:

Dla danej wartości N rozkład prawdopodobieństwa P(n) jest funkcją i nazywamy go rozkładem dwumiennym:

2. Rozkład normalny

K. F Gauss wprowadził dla szczególnego przypadku rozkładu dwumiennego postać będącą funkcją ciągłą, wyrażającą równaniem:

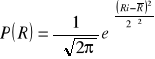
Ma ono dwa parametry:

- wartość średnia:

- odchylenie standardowe:

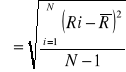
3. Opis układu pomiarowego

a) omomierz cyfrowy

b) rezystory fabryczne o rezystancji ok. 160
zamontowane w obudowie, gdzie każdy jest podłączony do osobnego gniazda pomiarowego.

II. WYKONYWANE CZYNNOŚCI I WYNIKI POMIARÓW

1. Przeprowadzenie eksperymentu

a) wykonać pomiary rezystancji rezystorów

b) pogrupować wyniki w przedziały o szerokości 0,5

2. Wyniki pomiarów

Wyniki pomiarów przedstawia tabela:

Tabela 1- Liczba rezystorów przypadająca na dany przedział rezystancji.

Lp.	Szerokość przedziału( )	Liczba rezystorów (xi)
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.	150-150,5 150,5-151 151-151,5 151,5-152 152-152,5 152,5-153 153-153,5 153,5-154 154-154,5 154,5-155 155-155,5 155,5-156 156-156,5 156,5-157 157-157,5 157,5-158 158-158,5 158,5-159 159-159,5 159,5-160 160-160,5 160,5-161 161-161,5 161,5-162 162-162,5 162,5-163 163-163,5 163,5-164 164-164,5 164,5-165	0 0 0 0 0 0 0 0 0 0 1 3 6 10 15 28 32 29 26 13 16 6 7 5 5 1 1 0 2 2

III. OBLICZENIA I ANALIZA DOKŁADNOŚCI WYNIKÓW

1. Wykonany schodkowy histogram zależności ilości rezystorów (xi) od numeru przedziału (ni) przedstawia wykres 1. Szerokość przedziału przyjąłem równą 0,5

2. Obliczone punkty pomocnicze na podstawie zależności Simpsona przedstawiłem w tabeli 2

Tabela 2 - Punkty pomocnicze na podstawie zależności Simpsona

Nr	Szerokość przedziału ( )	Punkt Simpsona
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29	155,5-156 156-156,5 156,5-157 157-157,5 157,5-158 158-158,5 158,5-159 159-159,5 159,5-160 160-160,5 160,5-161 161-161,5 161,5-162 162-162,5 162,5-163 163-163,5 163,5-164 164-164,5	3,25 6,25 10,25 17,00 25,75 30,25 29,00 23,50 17,00 12,75 8,75 6,25 5,50 4,00 2,00 0,75 0,75 1,50

3. Wykonany przypuszczalny kształt ciągłego rozkładu normalnego przedstawia wykres 2, gdzie przez x oznaczyłem pomocnicze punkty Simpsona

4. Wyznaczenie parametrów rozkładu:

a) wartość średnia

- ze wzoru:

- z wykresu:

b) odchylenie standardowe

- ze wzoru:

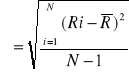
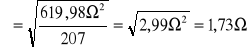
- z wykresu:

- z analizy równania zlogarytmowanego stronami:

wzory na regresję liniową:

nachylenie:

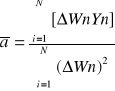
przesunięcie:

Tabela 3 - Obliczenia

						Yn		Wn			dWn
lp.	Ri	RiXi	Rs	Xi	Xi+1	ln(Xi+1)	(Ri-Rs)	(Ri-Rs)^2	Ws	Ys	Wn-Ws	dWn^2	dWn*Yn
1	155,5	156	159,15	1	2	0,69315	-3,649	13,3152	9,525	1,997	3,791	14,3679	2,6274
2	156	468	159,15	3	4	1,38629	-3,149	9,9162	9,525	1,997	0,392	0,15327	0,5427
3	156,5	939	159,15	6	7	1,94591	-2,649	7,0172	9,525	1,997	-2,508	6,28756	-4,8794
4	157	1570	159,15	10	11	2,3979	-2,149	4,6182	9,525	1,997	-4,907	24,0737	-11,765
5	157,5	2363	159,15	15	16	2,77259	-1,649	2,7192	9,525	1,997	-6,806	46,3148	-18,869
6	158	4424	159,15	28	29	3,3673	-1,149	1,3202	9,525	1,997	-8,205	67,3138	-27,627
7	158,5	5072	159,15	32	33	3,49651	-0,649	0,4212	9,525	1,997	-9,104	82,8737	-31,83
8	159	4611	159,15	29	30	3,4012	-0,149	0,0222	9,525	1,997	-9,503	90,2975	-32,32
9	159,5	4147	159,15	26	27	3,29584	0,351	0,1232	9,525	1,997	-9,402	88,3882	-30,986
10	160	2080	159,15	13	14	2,63906	0,851	0,7242	9,525	1,997	-8,801	77,4488	-23,225
11	160,5	2568	159,15	16	17	2,83321	1,351	1,8252	9,525	1,997	-7,7	59,2823	-21,814
12	161	966	159,15	6	7	1,94591	1,851	3,4262	9,525	1,997	-6,099	37,1917	-11,867
13	161,5	1131	159,15	7	8	2,07944	2,351	5,5272	9,525	1,997	-3,998	15,98	-8,3126
14	162	810	159,15	5	6	1,79176	2,851	8,1282	9,525	1,997	-1,397	1,95021	-2,5022
15	162,5	650	159,15	4	5	1,60944	3,351	11,2292	9,525	1,997	1,704	2,90532	2,7433
16	163	163	159,15	1	2	0,69315	3,851	14,8302	9,525	1,997	5,305	28,1483	3,6775
17	163,5	164	159,15	1	2	0,69315	4,351	18,9312	9,525	1,997	9,406	88,4822	6,5201
18	164	164	159,15	1	2	0,69315	4,851	23,5322	9,525	1,997	14,01	196,21	9,7093
19	164,5	329	159,15	2	3	1,09861	5,351	28,6332	9,525	1,997	19,11	365,135	20,993
20	165	330	159,15	2	3	1,09861	5,851	34,2342	9,525	1,997	24,71	610,559	27,146
Suma												1903,36	-152,04

Obliczam nachylenie:

Obliczam przesunięcie:

Wykresy pomocnicze:

8

---