WYDZIAŁ ELEKTRONKI TELEKOMUNIKACJI I INFORMATYKI KATEDRA OPTOELEKTRONIKI I SYSTEMÓW ELEKTRONICZNYCH LABORATORIUM PODSTAWY ELEKTRONIKI I MIERNICTWA GRUPA ..1/1.....
Ćwiczenie nr 1 Podstawowe mierniki i pomiary elektryczne	Imię i nazwisko
		Data wykonania ćwiczenia
		Data odbioru sprawozdania
		Ocena zaliczenia
		Uwagi i podpis

Cel ćwiczenia

Celem tego ćwiczenia było zapoznanie się z popularnymi przyrządami mierniczymi, oraz wykorzystanie ich do różnorakich pomiarów. Za ich pomocą dokonano wzorcowania woltomierza, amperomierza, pomiaru rezystancji, pomiaru mocy, oraz zestawiono w pełni funkcjonalny system pomiarowy bazujący na komputerze klasy PC. System ten umożliwiał zbieranie, gromadzenie, obróbkę i wygenerowanie określonych raportów pomiarowych.

Zadania pomiarowe

1. Wzorcowanie woltomierza

Po zestawieniu obwodu pomiarowego zgodnego ze schematem (rys. 13) przystąpiłem do wykonania ćwiczenia. W wyniku przeprowadzonych pomiarów uzyskałem następujące wyniki:

Ub [V]	0.2	0.4	0.6	0.8	1.0
Uw [V]	0.199	0.397	0.594	0.790	0.986
ε [mV]	1	3	6	10	14
δ [%]	0,502	0.755	1.010	1.265	1.419

Po wypełnieniu tabeli w wierszu U_w [V] należy obliczyć wpierw błędy bezwzględne wynikające z pomiarów.

Wzór na błąd bezwzględny miernika magnetoelektrycznego :

ε = |U_b - U_w|

gdzie :

U_b - wartość napięcia uzyskana woltomierzem magnetoelektrycznym

U_w - wartość napięcia uzyskana woltomierzem cyfrowym

I tak dla przykładu:

I kolumna

ε = 0.2 V - 0.199 V = 0.001 V = 1 mV

Następnie obliczamy wartości błędów względnych dla poszczególnych napięć - otrzymujemy je z poniższej zależności :

W przypadku I kolumny uzyskujemy :

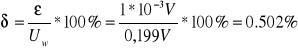
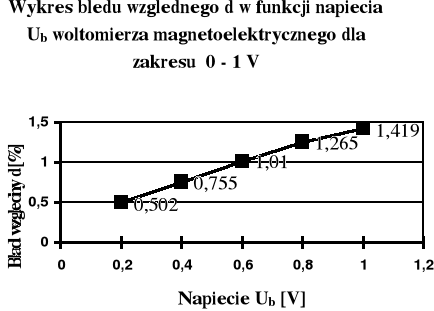
Z tego wykresu wynika, że najmniejsze wartości błędów względnych oscylowały mniej więcej w środku skali pomiarowej woltomierza magnetoelektrycznego.

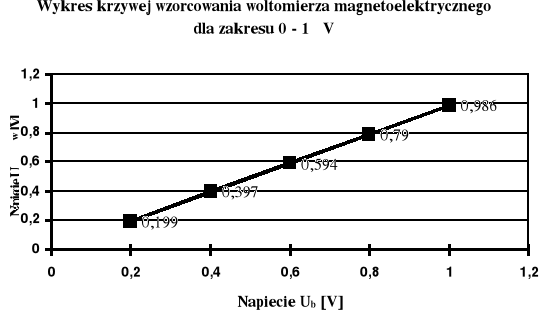
Charakterystyka napięcia mierzonego woltomierzem cyfrowym w funkcji napięcia mierzonego za pomocą woltomierza magnetoelektrycznego jest liniowa. Wskazania obu przyrządów nie są obarczone jakimiś większymi odchyleniami względem siebie.

Warto przy okazji sprawdzić, czy woltomierz magnetoelektryczny zachował podczas pomiarów swoją klasę dokładności. Opisuje to następująca zależność:

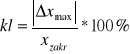
gdzie:

- maksymalny błąd bezwzględny ( błąd graniczny przyrządu)

- wartość końcowa zakresu pomiarowego

Tak więc:

Ponieważ badany woltomierz posiada klasę 1.5%, zaś wyliczona wartość wynosi 1.40%, można zatem powiedzieć, że podczas pomiarów przyrząd zachował swoje parametry.

Poza tym zauważyć trzeba, że woltomierz magnetoelektryczny nieznacznie zawyża wynik pomiarowy w stosunku do wzorcowego wyniku uzyskanego za pomocą laboratoryjnego woltomierza cyfrowego.

2. Zmiana zakresu pomiarowego woltomierza.

Następnym zadaniem było rozszerzenie zakresy pomiarowego woltomierza magnetoelektrycznego z 1 V do 4 V. Aby uzyskać żądany efekt, do badanego woltomierza należało podłączyć szeregowo posobnik (w naszym przypadku nastawny rezystor dekadowy R_p ) o znanej rezystancji (rys 15).

Aby wyliczyć tą rezystancję należy posłużyć się następującym rozumowaniem:

Przez posobnik i woltomierz przepływa ten sam prąd. W związku z tym można zapisać następującą zależność:

I_p = I_v = I_p+w

gdzie:

I_p - prąd płynący przez posobnik

I_v - prąd płynący przez woltomierz

I_p+v - prąd płynący przez układ posobnik + woltomierz

Z kolei prąd woltomierza I_w opisuje następujący związek:

gdzie:

U_v - napięcie na zaciskach woltomierza

R_v - rezystancja wewnetrzna woltomierza

Prąd I_v+p przepływający przez układ woltomierza i posobnika:

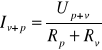
gdzie :

U_p+v - napięcie na zaciskach układu posobnik + woltomierz

R_p + R_v - wypadkowa rezystancja układu posobnik + woltomierz

Przyrównujemy teraz obie zależności:

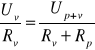
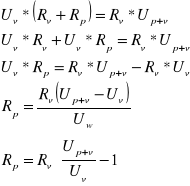
Iloraz
wskazuje nam, ile razy zwiększył się zakres mierzonego napięcia, dlatego określa się go jako mnożnik zakresu pomiarowego i oznacza n. Stąd nasz wzór ostatecznie przyjmie postać:

W moim przypadku chcę zwiększyć zakres pomiarowy z 1 V do 4 V, tak więc

U_p+v = 4 V, U_v = 1 V, a wartość n wyniesie:

Po podstawieniu do wzoru na wartość rezystancji posobnika otrzymujemy:

R_p = 20 000 Ω *( 4-1 ) = 60 000 Ω

Zatem chcąc zwiększyć zakres pomiarowy czterokrotnie należy podłączyć szeregowo posobnik o rezystancji równej czterokrotnej wartości rezystancji wewnętrznej woltomierza rozszerzanego. Tak też uczyniłem i przystąpiłem do pomiarów napięć celem ustalenia błędów względnych przyrządu o rozszerzonym zakresie pomiarowym, oraz wyznaczenia krzywej wzorcowania. Na końcu należy jeszcze sprawdzić, czy tak „udoskonalony” przyrząd zachował swoją klasę pomiarową.

Po wypełnieniu wiersza U_w [V] pomierzonymi napięciami obliczamy kolejno błędy bezwzględne i względne dla poszczególnych napięć (zgodnie ze wzorami z punktu 1).

Ub [V]	0.8	1.6	2.4	3.2	4.0
Uw [V]	0.793	1.591	2.384	3.164	3.949
ε [mV]	7	9	16	36	51
δ [%]	0,882	0.565	0,671	1.137	1.291

Następnie wyznaczamy krzywą wzorcowania dla woltomierza o rozszerzonym zakresie.

Podobnie jak w przypadku zakresu pomiarowego 0 - 1 V tak i w tym przypadku wykres jest liniowy - dołączenie posobnika nie wpłynęło zasadniczo na zmianę charakterystyki U_w / U_b.

Porównując oba wykresy błędów względnych (dla zakresu 0 - 1 V oraz 0 - 4V) zauważyć można następującą prawidłowość:

- dla zakresu napięcia 0-4V wskazania napięć od początku do środka skali są wyraźnie obarczone większymi błędami pomiarowymi niż w przypadku zakresu 0-1V.

- od środka do końca skali pomiarowej są zbliżone, jednakże z lekką „przewagą” zakresu 0-4V (mniejsze błędy)

Sprawdzić jeszcze należy, czy woltomierz z rozszerzonym zakresem zachował swoja klasę dokładności.

gdzie:

- maksymalny błąd bezwzględny ( błąd graniczny przyrządu)

- wartość końcowa zakresu pomiarowego

Dla zakresu 4V maksymalny błąd bezwzględny wynosi 51 *10 ^-3 V, tak więc

Woltomierz posiada klasę pomiarową 1.5%, zaś wyliczona z pomiarów wynosi 1.275%.

Można zatem stwierdzić, że przyrząd zachował swoja klasę pomiarową - co więcej, w stosunku do poprzednich pomiarów na zakresie 0-1V (1.40% ) nawet uzyskał nieznacznie lepszy wynik.

Podobnie jak to miało miejsce w przypadku zakresu pomiarowego 0 - 1 V woltomierz magnetoelektryczny nieznacznie zawyżał wyniki pomiaru w stosunku do wzorcowego wyniku uzyskanego przez laboratoryjny woltomierz cyfrowy.

3. Pomiary prądu stałego amperomierzem cęgowym

Po zestawieniu obwodu pomiarowego zgodnie z rys. 16 przystąpiłem do wykonywania pomiarów. Wyniki umieściłem w tabelce (wiersz I_w [mA])

Ib [mA]	50	100	150	200	250	300
Iw [mA]	56	106	156	204	254	304
ε [mA]	6	6	6	4	4	4
δ [%]	10,714	5,660	3,846	1,960	1,574	1,315

Należy teraz wyliczyć błąd bezwzględny dla poszczególnych wartości prądu:

ε = |I_b - I_w|

gdzie:

I_b - wartość prądu zmierzona amperomierzem cęgowym

I_w - wartość prądu zmierzona wzorcowym amperomierzem cyfrowym

Dla przykładu:

Prąd 50 mA ε = |I_b - I_w | = |50 mA - 56 mA| = 6 mA = 6 mA

Następnym krokiem jest wyliczenie wartości błędu względnego dla danych prądów.

Podstawiamy więc wyliczone wartości błędów bezwzględnych do wzoru:

Przy prądzie I_b = 50 mA wartość błędu względnego wyniesie:

Jak wynika z wykresu, charakterystyka zależności I_w / I_b jest liniowa. Podobnie zresztą prezentowały się charakterystyki napięciowe woltomierzy - stąd wniosek, że wskazania amperomierza cęgowego w całym przedziale skali są liniowe, choć obarczone niewielkim błędem.

Daje się zaobserwować interesującą zależność - im większa wartość prądu tym mniejsza wartość błędu względnego. Przy wartości prądu 50 mA próg błędu wynosi 10,714% i przy zwiększaniu wartości prądu próg błędu obniża się i przy 300mA wynosi 1,315%.

4. Pomiar rezystancji multimetrem cyfrowym

Ćwiczenie polegało na pomiarze wartości pięciu rezystorów za pomocą miernika cyfrowego.

Wyniki pomiarów umieszczone są w tabeli:

Nr rezystora	1	2	3	4	5
Ri [kΩ]	9.91	9.72	10.26	9.84	10.17

Na podstawie tych danych należy teraz obliczyć wartość średnią, odchylenie standardowe pojedynczego pomiaru oraz odchylenie standardowe wartości średniej, ilustrujące właściwości statystyczne populacji.

Wartość średnia rezystancji tej serii rezystorów wyraża się wzorem:

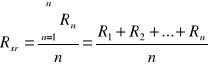
gdzie:

n - liczba rezystorów (w naszym przypadku 5)

R_n - wartość n - tego rezystora

Po podstawieniu do wzoru otrzymujemy:

= 9.980 kΩ

W pomiarze za pomocą komputera wyliczona przezeń wartość rezystancji jest równa wynikowi moich obliczeń (9.980 kΩ). Porównując poszczególne wartości rezystancji pomierzone przez komputer zauważyłem, że wartość pomiaru każdego rezystora jest równa wartości uzyskanej przeze mnie w pomiarze manualnym.

Obliczamy teraz odchylenie standardowe pojedynczego pomiaru, które wyraża się wzorem:

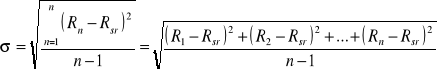
gdzie:

R_n - wartość rezystancji n - tego rezystora badanej serii

R_sr - wartość średnia rezystancji badanej serii

n - liczba rezystorów w badanej serii

Po podstawieniu do wzoru otrzymujemy:

Wartość tego odchylenia dla pomiaru manualnego wynosi (w zaokrągleniu)  0.227 kΩ , a wartość wyliczona przez komputer wyniosła również 0.227 kΩ.

Następną wartością, która należało wyliczyć, było odchylenie standardowe wartości średniej.

Wyliczamy tą wielkość z następującej zależności:

gdzie:

σ - odchylenie standardowe pojedynczego pomiaru

n - liczba pomiarów (rezystorów)

Po podstawieniu otrzymujemy:

 Tutaj również wyliczona przeze mnie wartość ( 0.102 kΩ ) jest identyczna do wartości wyliczonej przez komputer ( 0.102 kΩ ).

6. Pomiar mocy

Celem tego ćwiczenia był pomiar mocy wydzielanej na rezystorze - elemencie o znanej rezystancji, a następnie porównanie przeprowadzonych obliczeń z wynikami otrzymanymi za pomocą układu AD 7755 - specjalizowanego układu cyfrowego do pomiaru energii elektrycznej i mocy. W dalszej części ćwiczenia zamiast rezystora o znanej wartości podłączymy żarówkę, następnie wyliczymy wydzielającą się na niej energię i porównamy z wynikami uzyskanymi przy pomocy w/w układu scalonego.

Po podłączeniu układu pomiarowego według schematu z rysunku 17 dokonałem pomiarów częstotliwości, otrzymanych na wyjściu f_wy . Wyniki umieściłem w tabelce:

U [V]	0.5	1.00	1.5	2.0	2.5	3.0	3.5	4.0
f [kHz]	0.050	0.200	0.450	0.799	1.250	1.799	2.450	3.200
P [mW]	2.5	10	22.5	40	62.5	90	122.5	160
k [mW/kHz]	50	50	50	50.062	50	50	50.027	50

Aby obliczyć moc wydzielającą się na rezystorze R_L = 100 Ω należy użyć wzoru na moc czynną:

P = u * i * cos ϕ [W]

gdzie:

u - napięcie skuteczne [V]

i - prąd skuteczny [A]

cos ϕ - wartość (kąt) przesunięcia fazowego między napięciem u i prądem i

W naszym przypadku nie znamy wartości kąta przesunięcia fazowego, lecz przy obciążeniach typowo rezystancyjnych (a za takie możemy uznać zarówno rezystor jak i żarówkę) wartość przesunięcia fazowego pomiędzy napięciem skutecznym i prądem skutecznym wynosi 0 (mówi się, że w takim przypadku napięcie jest w „fazie” z prądem).

Dla kąta ϕ = 0 otrzymujemy wartość przesunięcia fazowego cos ϕ = 1.

Dzięki temu nasz wzór upraszcza się do postaci:

P = u * i , i = u / R

a po jego rozwinięciu otrzymujemy zależność:

którą użyjemy do obliczenia mocy wydzielanej na danej rezystancji (w ćwiczeniu - R_L ).

Dla przykładu, obliczenia dla pierwszej kolumny „0.5 V” będą wyglądały następująco:

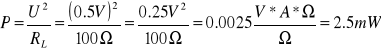
Następnie należy uzupełnić tabelę w wierszu „k [mW/kHz]” - jest to współczynnik przetwarzania układu do pomiaru mocy i wyraża się zależnością:

Wyliczenie wartości k dla pierwszej kolumny będzie wyglądało tak:

Ponieważ współczynnik k jest w „przybliżeniu” taki sam dla różnych wartości napięcia, można założyć, że charakterystyka częstotliwości wyjściowej układu w funkcji mocy jest liniowa. Aby potwierdzić te przypuszczenie należy sporządzić wykres zależności f_wy = f(P)

Wykres jest zgodny z moimi przypuszczeniami - dla danego układu pomiarowego charakterystyka przetwarzania P/f (moc / częstotliwość) jest liniowa.

W drugiej części ćwiczenia w miejsce rezystora o znanej rezystancji podłączyliśmy żarówkę.

Celem ćwiczenia był pomiar energii pobranej przez to obciążenie, mierzonej przy dwóch różnych wartościach napięcia zasilającego. W wyniku dokonanych pomiarów otrzymałem następujące wyniki:

I pomiar:

Czas pomiaru t - 50 sekund (
)

Napięcie zasilające U - 2.000 V

Prąd pobierany przez żarówkę I - 25.8 mA

II pomiar:

Czas pomiaru t - 50 sekund (
)

Napięcie zasilające U - 4.000 V

Prąd pobierany przez żarówkę I - 38.2 mA

Ogólny wzór na energię pobraną przez odbiornik wygląda następująco:

E = P*t [kWh, mWh]

W naszym przypadku można zapisać, że

E = U * I * t

Tak więc dla pierwszego pomiaru wyliczona wartość wyniesie :

E₁ = 2.000 V * 25.8 mA * 5/360 h = 0.716667 mWh

Dla drugiego pomiaru:

E₂ = 4.000 V * 38.3 mA * 5/360 h = 2.122222 mWh

Porównując to z wartościami uzyskanymi i wyliczonymi przez komputer daje się zauważyć nieznaczne odchylenia od uzyskanych przeze mnie wyników (komputer odpowiednio I pomiar - 0.700 mWh, oraz II pomiar - 2.004 mWh). Bierze się to z zaokrągleń, którymi posługiwałem się podczas obliczania wartości mocy (wartość prądu), podczas gdy komputer z dużą dokładnością i precyzją zliczał i sumował pobraną energię na bieżąco. Jak więc widać, automatyzacja pomiaru pozwala na precyzyjniejsze, a co najważniejsze, na natychmiastowe uzyskanie odpowiednich wartości bez potrzeby dalszych, czasami żmudnych obliczeń.

Należy także zauważyć jedną prawidłowość - dwukrotne zwiększenie napięcia nie spowodowało czterokrotnego zwiększenia się wydzielanej mocy, a co za tym idzie czterokrotnego zwiększenia się pobranej energii. Przy stałej rezystancji taki fakt powinien mieć miejsce, jednakże tak się nie stało. Przeprowadzając odpowiednie obliczenia dla pierwszego pomiaru wyliczamy, że żarówka posiadała rezystancję równą:

Natomiast dla drugiego pomiaru rezystancja żarówki wyniosła:

Wzrost rezystancji żarówki spowodowany został fizycznymi własnościami włókna wolframowego, z którego żarówka jest zbudowana (materiał nagrzewając się zwiększa swoją rezystancję)- stąd też różnice między wartościami teoretycznie oczekiwanymi, a faktycznie uzyskanymi.

---